お気軽にお問い合わせください
因果推論の定番手法”差分の差分法”について詳しく解説!

社会科学、医療、ビジネスなど幅広い分野における効果測定の手法として、因果推論が注目を集めています。
単純な介入前後の数値比較では、季節変動や市場トレンドの影響を排除できず、真の成果を見誤るリスクがあります。介入の「真の効果」を測定するには、「介入を実施した結果(現実)」と、「介入を実施しなかった場合の結果(反実仮想)」を比較する必要があります。
因果推論の定番手法である差分の差分法(Difference in Differences:DID)は、この「もし介入を実施しなかったら」という状態を統計的に推計し、真の効果を明らかにすることが可能です。
本記事では、DIDの概念から具体的な分析手順、ビジネスシーンでの活用事例までを網羅し、その全体像を詳しく解説します。
差分の差分法とは
因果推論は、相関関係ではなく因果関係を明らかにするための手法であり、介入効果を評価する際に、介入群と対照群を設定します。それぞれのアウトカムを比較することで、単なる相関ではなく、介入がもたらしたと考えられる因果的な効果を推定することが可能になります。
しかし、介入後の介入群と対照群のアウトカムを比較するだけでは、介入効果を正しく評価できません。
その理由は主に2つあります。
- 理由1. 時間変化によるバイアスを考慮できていない
-
例えば、マーケティング施策による売上変化をアウトカムとする場合、会社全体として売上が右肩上がりであると、売上の増加が施策の影響か、時間的なトレンドの影響かを区別できません。
- 理由2. グループ間の水準によるバイアスを考慮できていない
-
例えば、介入群に大型店が多く、対照群に中規模店が多い場合、もともとの売上水準が異なるため、施策効果を過大評価してしまう可能性があります。
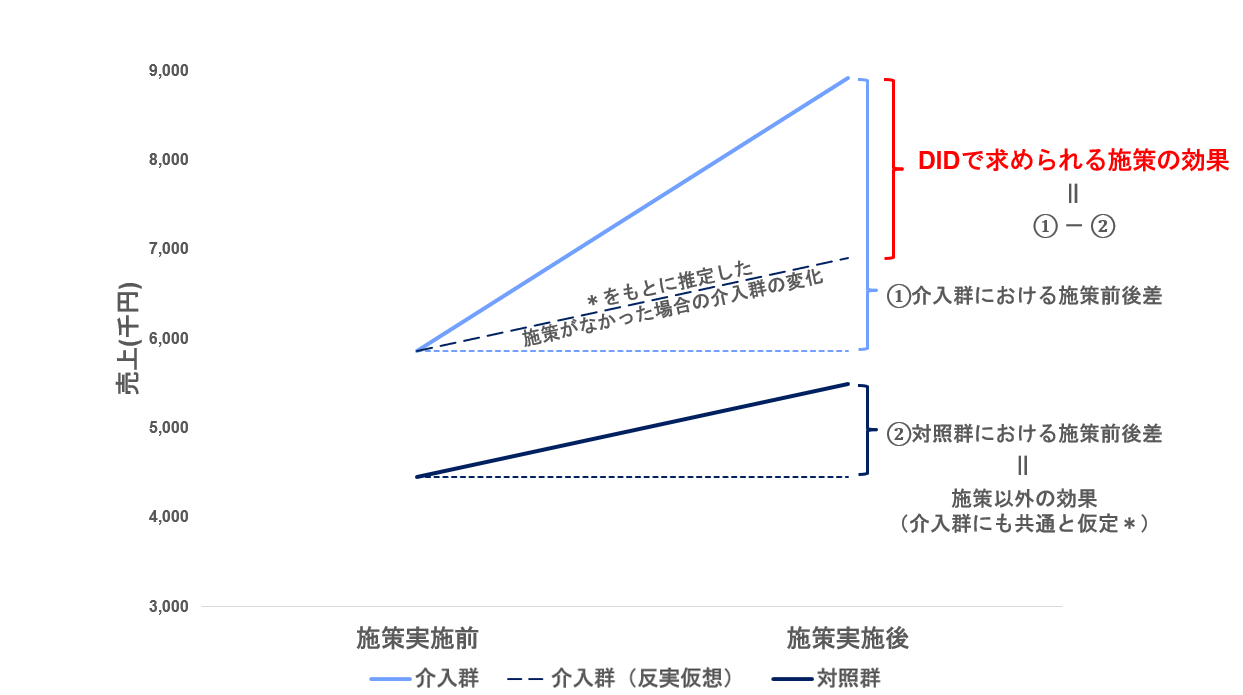
この2つのバイアスに対応できるのがDIDです。介入前後の“差”を取り、さらに介入群と対照群の“差”を取ることで、介入による因果効果をより正確に推定することができます。
- 相関関係 / 因果関係
- 相関関係:2つの事象が連動して動いて見える関係
- 因果関係:ある事象が別の事象を引き起こす原因と結果の関係
- 介入群 / 対照群
- 介入群:介入を実施するグループ
- 対照群:介入を実施しないグループ
- 2つのグループを比較することで、介入の効果を統計的に評価し、因果効果を推定することが可能
- アウトカム
- 介入によって変化する観測対象の変数
- 例:マーケティング施策における売上やクリック数、薬の投与における症状の改善度など
DIDの分析手順
以降では、ビジネス施策を例に挙げて、DIDを実施する際の基本的な流れと具体的な推定方法を紹介します。
DIDの基本的な流れ
DIDを実施するには、施策の前後で比較できるデータが必要です。
その中でも、アウトカムは施策によって変化すると想定され、かつ収集・定量化が可能な変数である必要があります。
例えば、施策として実施したクーポン配布の効果を評価したい場合は、売上や来店数などを用いて評価することが適切であるため、これらのデータを複数店舗に対して一定期間集めます。
既に継続してデータを集めている場合など、手元に過去のデータがある場合はこのステップは不要です。
平行トレンドの仮定を満たすように、観測したサンプルを介入群と対照群に設定します。
平行トレンドの仮定とは、介入群と対照群において、施策以外の要因によるアウトカムの変化が共通していると仮定するものであり、DIDを用いる上で必ず確認すべき前提です。この詳細については「分析上の注意点」にて説明します。
施策前のデータを見比べ、両群のアウトカムの推移が大きく異なる場合には、介入群と対照群を再度設定し、平行トレンドの仮定を確認します。
また、店舗の規模や利用客の性別、年齢層などの属性がアウトカムに影響を与えることがあるので、両群の間で属性が大きく異ならないようにサンプルを選ぶことが推奨されます。
施策開始後の両群におけるアウトカムのデータを継続して集めます。
集めたデータは以下のイメージになります。
| 店舗ID | 年月 | 介入群 / 対照群 | 売上(千円) |
|---|---|---|---|
| 1 | 2022年1月 | 対照群 | 3,000 |
| 2 | 2022年1月 | 介入群 | 2,200 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 1 | 2024年12月 | 対照群 | 3,100 |
| 2 | 2024年12月 | 介入群 | 4,200 |
| ⋮ | ⋮ | ⋮ | ⋮ |
DIDにおける因果効果は、主に次の2つの方法で推定できます。
- 差分の差分を計算する(四則演算)
介入群のアウトカム変化量から、対照群のアウトカム変化量の差分を取ります。
これが「差分の差分」であり、DIDが推定する施策の因果効果です。 - 統計モデルで推定・検定する
アウトカムを目的変数、介入群ダミー・時点ダミー・交互作用項を説明変数とした回帰分析をおこない、DIDを統計的に推定します。
これにより、単純な差分の計算だけでなく、統計的な有意性を確認することができます。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。差分の差分法(DID)をはじめ、因果推論による分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
DIDの推定方法
ここでは「Step 4. 因果効果を推定する」で説明したDIDによる因果効果の推定方法について紹介します。
具体例として、割引クーポンの配布が売上に与える因果効果を推定する場合を考えます。
介入群を地域Aの店舗、対照群を地域Bの店舗として設定し、それぞれのグループで施策前後の売上を比較します。
施策の実施は2024年7月とし、地域Aと地域Bにおける店舗数や規模、顧客構成などの属性は類似していると仮定します。
四則演算におけるDID
地域A,Bにおけるクーポン配布前後1ヶ月の平均売上が以下であったとします。
| 地域 | クーポン配布前の売上(千円) | クーポン配布後の売上(千円) | 売上の変化(千円) |
|---|---|---|---|
| 地域A(介入群) | 5,800 | 8,900 | +3,100 |
| 地域B(対照群) | 4,500 | 5,100 | +600 |
DIDを用いずにクーポン配布の効果を推定すると、以下のようになります。
- パターン①
- 地域Aにおける、クーポン配布前後の比較
- 8,900 – 5,800 = +3,100
- パターン②
- クーポン配布後の地域Aと地域Bの比較
- 8,900 – 5,100 = +3,800
パターン①では、時間的トレンドによるバイアスを考慮できていません。実際には、クーポン配布による効果ではなく、季節要因などによって売上が上昇した可能性があります。
パターン②では、水準の違い(地域差)によるバイアスを考慮できていません。地域Aはもともと地域Bより売上水準が高い可能性があり、その差を無視して比較してしまっています。
一方でDIDを用いて、クーポン配布の効果を推定すると以下のようになります。
$$
\begin{aligned}
&DID =① (Y_{介入群,施策後} – Y_{介入群,施策前}) \ – \ ②(Y_{対照群,施策後} – Y_{対照群,施策前})\\
&DID = (8,900 \ – \ 5,800) \ – \ (5,100 \ – \ 4,500)\\
&DID = 3,100 \ – \ 600 = 2,500\\
\end{aligned}
$$
①地域Aの売上の変化は+3,100千円であるのに対し、②地域Bの売上の変化は+600千円です。これらの差分をとり、クーポン配布による効果は+2,500千円と推定できます。
クーポン施策は短期的に購買行動へ影響すると考えられるため、クーポンを配布して売上に変化が表れるまで、時間はかからないと想定されます。したがって、今回の例では、施策の直前直後で比較をおこないました。
一方で、施策の効果が表れるまでに時間がかかると考えられる場合は、施策直後のデータを分析から除外することが推奨されます。 過渡期のデータを含めて効果を推定すると、平均すると大きな効果がないという誤った結論(過小評価)に至るリスクがあるためです。
施策の内容に応じて、効果が現れるまでのリードタイムを適切に見積もり、分析期間を設定することが重要です。
統計モデルにおけるDID
代表的な手法として回帰分析におけるDIDについて説明します。
DIDを回帰分析で使用するには、以下の変数が必要になります。
- 目的変数:アウトカム(売上)
- 説明変数:介入ダミー、時点ダミー、それらを掛け合わせた交互作用項
回帰式は以下になり、DIDの効果は交互作用項の係数\(b_{DA}\)で表されます。
$$Y_{it} = b_0 + b_DD_i + b_AA_t + b_{DA}( D_i × A_t ) + u_{it}$$
$$
\begin{aligned}
&i:店舗i \\
&t:時点t \\
&Y_{it}:時点tにける店舗iの売上 \\
&D_i:介入ダミー(店舗iにクーポンが配布されたかを表す) \\
& D_i = 0:クーポン配布なし \\
& D_i = 1:クーポン配布あり \\
&A_t:時点ダミー(施策の前後を表す) \\
& A_t = 0:クーポン配布前 \\
& A_t = 1:クーポン配布後 \\
&u_{it}:誤差項 \\
\end{aligned}
$$
四則演算におけるDIDでは施策実施の前後1ヶ月のデータのみを用いましたが、回帰分析では複数時点のデータを使用します。
収集した24年1月から24年12月までのデータ全て用いて回帰分析をおこない、結果をまとめると以下のような表になります。
| 説明変数 | 係数(千円) | p値 |
|---|---|---|
| 切片(\(b_0\)) | 4,310 | 0.0 |
| 介入ダミー(\(b_{D}\)) | 1,670 | 0.05 |
| 時点ダミー(\(b_{A}\)) | 1,060 | 0.25 |
| 交互作用項(\(b_{DA}\)) | 2,300 | 0.05 |
上記の表から、\(b_{DA}\)の係数がプラスかつ、p値が十分に小さく有意であるので、クーポン配布により売上が上昇し、その効果は約+2,300千円と推定できます。
その他手法におけるDID
- ・差分の差分の差分法(DDD)
-
DIDでは時点×施策の2軸による比較でしたが、DDDでは時点×施策×商品カテゴリのように、もう1軸加えて因果効果を推定できます。
- ・非線形モデル(ロジスティック回帰やポアソン回帰)
-
アウトカムが二値(購買するか否か)である場合や、カウントデータ(購入回数など)である場合には、非線形モデルによるモデリングが適切です。線形モデルに限らず、非線形モデルにおいてもDIDを活用できます。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。差分の差分法(DID)をはじめ、因果推論による分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
必要なデータ
DIDを実施するためには、売上などのアウトカムが定量データとして計測可能であることが前提となります。
また、分析に必要なデータ数として最低でも4点(施策前後の2時点×介入群・対照群となる2グループ)が必要です。
「DIDの推定方法」で提示したデータは以下のようなイメージになります。
| 店舗ID | 年月 | 地域 | 売上(千円) |
|---|---|---|---|
| 1 | 2024年1月 | B | 1,000 |
| 2 | 2024年1月 | A | 4,500 |
| 3 | 2024年1月 | A | 2,500 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 1 | 2024年12月 | B | 3,100 |
| 2 | 2024年12月 | A | 4,200 |
| 3 | 2024年12月 | A | 4,600 |
| ⋮ | ⋮ | ⋮ | ⋮ |
回帰分析では、年月や地域といった質的変数をそのまま扱うことができないため、ダミー変数化処理によって数値に変換します。
具体的には、施策が開始された瞬間から施策実施後として扱うため、施策を実施した2024年7月以降を1、2024年6月以前を0とする「時点ダミー」を作成します。
同様に、施策を実施した地域Aの店舗を1、実施していない地域Bの店舗を0とする「介入ダミー」も作成します。
さらに、DIDではこれら2つのダミー変数を掛け合わせた交互作用項も作成します。
| 店舗ID | 時点ダミー | 介入ダミー | 交互作用項 (時点ダミー×介入ダミー) | 売上(千円) |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1,000 |
| 2 | 0 | 1 | 0 | 4,500 |
| 3 | 0 | 1 | 1 | 2,500 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 1 | 1 | 0 | 0 | 3,100 |
| 2 | 1 | 1 | 1 | 4,200 |
| 3 | 1 | 1 | 1 | 4,600 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
データ収集時における注意点については、「分析上の注意点」にて解説いたします。
ビジネス活用事例
次にビジネス活用事例について紹介します。
マーケティング施策の評価
MMM(マーケティング・ミックス・モデリング)は、マーケティング施策の効果を定量的に評価できる手法で、KPIを最大化するように、広告予算配分を最適化が可能になります。
さらに、DIDを用いることで、最適化された予算配分がKPIの上昇にどの程度寄与したかを検証することができます。
例えば、アウトカムを「店舗での合計売上高」とし、平行トレンドの仮定を満たすように、地域単位で介入群と対照群を設定します。
介入群の広告出稿にはMMMを用いて導出した予算配分を適用し、対照群には従来の経験則に基づく予算配分を適用します。
十分な期間データを収集した後にDIDを実施します。
その結果、介入群と対照群で購入数に有意な差があった場合、最適化された予算配分による広告出稿が効果的であると結論付けることができます。この結果を踏まえて、最適化された予算配分を全国に採用するなど、統計的根拠に基づいたマーケティング施策の意思決定が可能です。


オンライン+オフライン施策の評価
ある特定の地域で実施されたオフライン施策についてもDIDを用いて評価することが可能です。
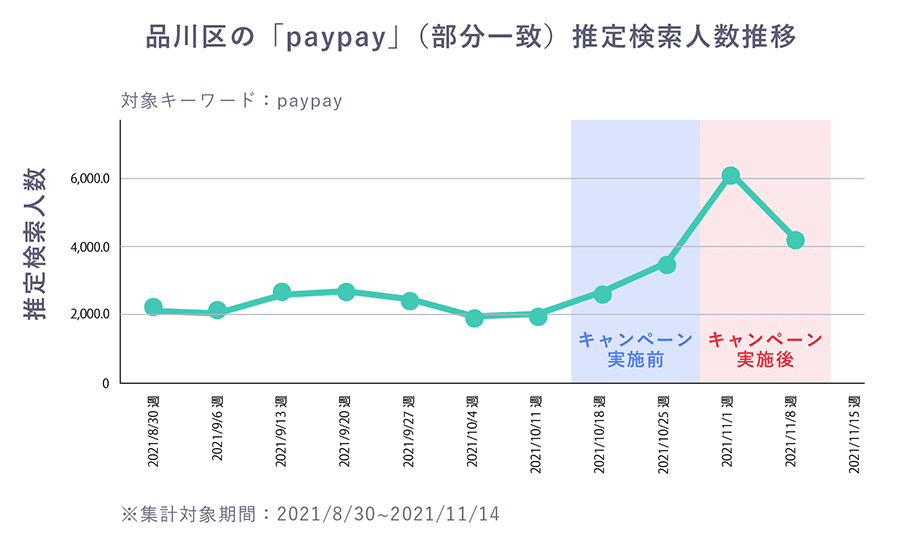
2021年11月に品川区で実施されたPayPayキャンペーンでは、アプリ上のポップといったオンライン施策だけでなく、ポスター掲示といったオフラインでの施策もおこなわれました。地域住民の関心・認知度の代理指標として、”キャンペーンの関連キーワード検索数”を用いることで、オンライン+オフライン施策を評価することが可能です。
施策前後の検索数の変化をDIDで比較することで、特定の地域での認知向上効果を全国的なトレンドの影響を除いて、統計的に推定することができます。この分析により、キャンペーン期間中、検索数が有意に増加していることが確認され、施策が地域における関心や認知の向上に寄与したと結論づけることができます。
社会政策の評価
ペンシルベニア大学の研究チームが低・中所得国で実施された現金給付プログラムの効果を分析しました。DIDを用いて現金給付の前後比較と、現金給付がなかった国との比較をおこない、妊婦の早期受診、ワクチン接種、栄養状態など17項目の母子保健・児童健康指標を用いて施策を評価しました。
その結果、妊娠初期における医療機関受診率の向上や、ワクチン接種率の向上など、母子ともに健康指標の改善が確認されました。現金給付による経済的な余裕が生まれ、ワクチン接種や十分な食事、衛生的な生活など、健康的な選択が可能になった可能性が示唆されます。
統計的根拠に基づき、DIDを用いて施策を評価し、社会への影響を明らかにすることで、政策設計や社会施策への応用が期待されます。
<参考>
Richterman, Aaron et al. (2025). “The effects of government-led cash transfer programmes on behavioural and health determinants of mortality: a difference-in-differences study”. The Lancet, Volume 406, Issue 10520, 2656 – 2666. https://doi.org/10.1016/S0140-6736(25)01437-0
分析上の注意点
最後にDIDの注意点についてご紹介いたします。
平行トレンド仮定
平行トレンド仮定とは、介入群と対照群において、施策以外の要因によるアウトカムの変化が共通であるとする仮定であり、DIDを用いる上で必ず確認すべき前提です。
施策効果を正確に評価するために、介入群の施策実施前後のアウトカムの変化から、時間的なトレンドといった施策以外の要因による影響を除く必要があります。
しかし、介入群における施策以外の要因による影響(施策を受けなかった場合のアウトカム)は観測できません。
そこで、介入群が施策を受けなかった場合のアウトカム変化を対照群から推定します。
介入群と対照群で、施策を受けなかった場合のアウトカム変化が同じであると仮定することで、介入群におけるアウトカム変化から、対照群のアウトカム変化(施策以外の要因による変化)を除くことができるため、正確に施策効果を評価することが可能です。
この仮定が成立しない場合、介入群と対照群で施策以外の要因による変化が異なってしまうため、施策の純粋な効果を正確に測定できず、DIDによる推定値にバイアスが含まれてしまう可能性があります。
平行トレンド仮定の確認方法はいくつかあります。
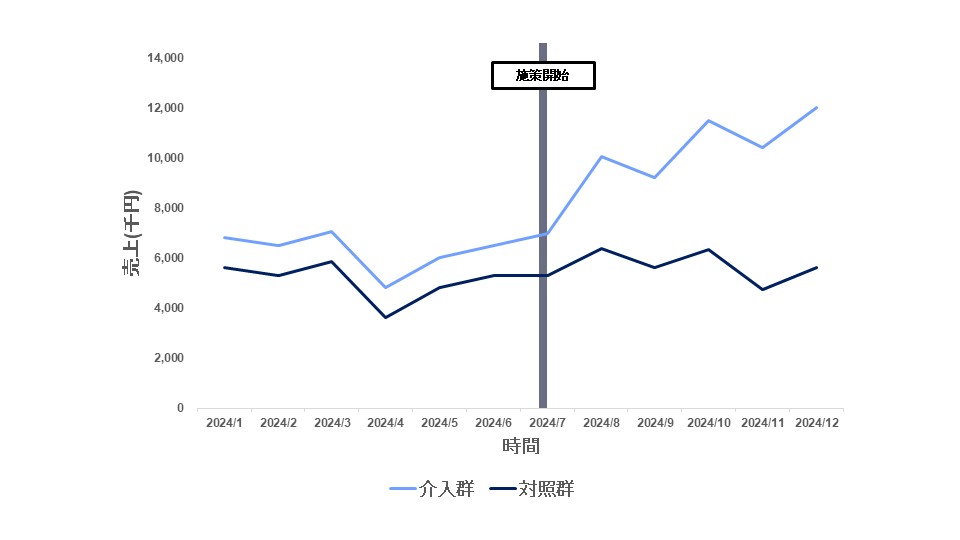
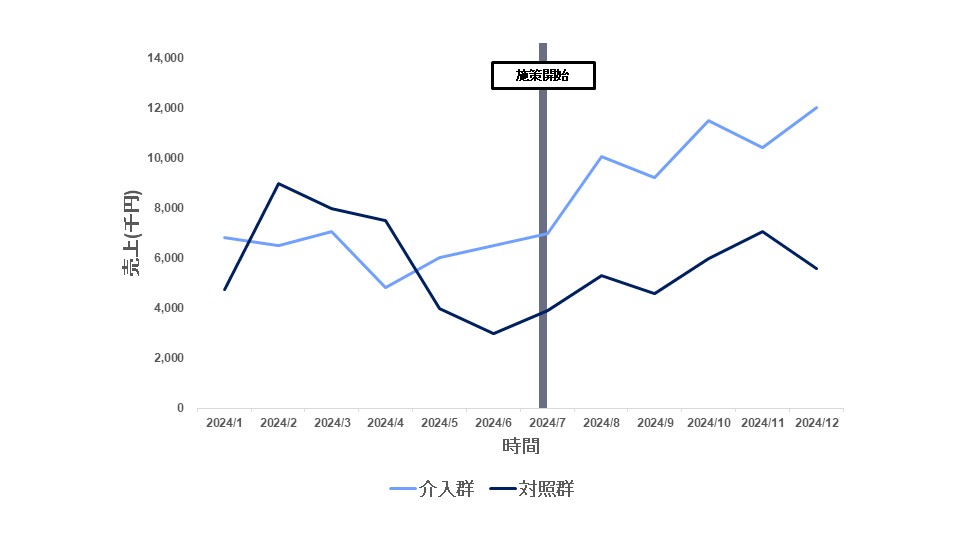
- 視覚的確認
施策実施前の期間における介入群と対照群のアウトカム推移をグラフで比較し、トレンドが同様かを確認する。 - 共通インパクトの確認
施策実施期間に、一方の群にのみ影響を与えるイベントや外部要因が発生していないかを確認する。
仮定が満たされない場合は、以下の対処法が有効です。
- 介入群・対照群の割り当てを再検討する
介入群と対照群のサンプル割り当てを再検討し、平行トレンドの仮定が満たされるようにサンプルを割り当て直します。 - 比較する期間を再検討する
施策実施前として使用する期間は、施策実施の直前が最善ですが、平行トレンドの仮定を満たさない場合は、平行トレンドの仮定が満たされる別の期間を比較対象期間とすることも可能です。 - 以下の手法との併用を検討する
- 合成コントロール法
- 仮想的にトレンドが一致する対照群を構築することが可能です。
- 傾向スコアマッチング
- 属性の違いによるトレンド差を緩和できる可能性があります。
- 合成コントロール法
データの収集
「必要なデータ」で記載したように、DIDを実施するためには、売上などのアウトカムとなるデータが最低限でも4点(施策前後の2時点×介入群・対照群となる2サンプル)が必要です。
しかし、時点数やサンプル数が少ないと平行トレンドの仮定を確認できなかったり、偶然性を排除することができず、推定の信頼性が低くなってしまいます。
そのため、DIDを用いて正確な効果を推定するためには、複数時点における複数サンプルのデータが必要になります。
データ収集時の注意点として以下があげられます。
- ・同一のサンプルを追跡すること
-
複数時点にわたり同一のサンプルを継続して追跡することが重要です。
時点ごとに異なるサンプルのデータを収集してしまうと、規模や顧客構成といったサンプルの属性が変わってしまい、施策の影響ではない差が生じ、推定結果にバイアスが含まれてしまう可能性があります。 - ・十分な期間の時系列データを収集すること
-
特に施策実施前のデータが十分な期間揃っている必要があります。
これは、前述の平行トレンド仮定を確認するためであり、施策前後を含め、十分な期間のデータを確保することが理想です。 - ・施策前後で観測方法や定義が一貫した同質なデータであること
-
例えば、アウトカムを売上とする場合、施策前後で計上のルールが変わると、DIDで推定した効果が施策による影響なのか、売上計上ルールの違いに起因する影響なのかを区別することができません。
したがって、観測経路やデータ収集手段、指標の定義などが施策の前後で同じである必要があります。 - ・欠損データの管理
-
観測・収集したデータに欠損が含まれていると、推定に偏りが発生する可能性があります。
DIDによる推定を頑健なものにするため、欠損が発生した理由を把握し、適切な処理をおこなう必要があります。例えば、閉店により観測が途中で途切れてしまった店舗は分析から除外したり、ある店舗の1ヶ月だけ売上データが欠損している場合は線形補完などで対処することが推奨されます。
- ・共変量の収集
-
共変量とは、施策とは直接関係しないが、アウトカムに影響を与える可能性があるサンプルごとの属性や外的要因などを示す変数です。
データを収集する際はアウトカムとして使用するデータだけではなく、共変量も同時に収集することが推奨されます。
収集した共変量は、回帰分析によるDIDの推定や傾向スコアマッチングを用いた介入群・対照群の割り当ての際に活用でき、バイアスを低減できる可能性があります。
まとめ
差分の差分法(Difference in Differences:DID)は因果推論の手法の一つであり、時間変化によるバイアスとグループ間の水準によるバイアスを考慮し、介入による因果効果をより正確に推定することが可能な手法です。
実務では十分な量のデータや、平行トレンドの仮定の確認など、前提となる条件を満たすことが重要です。適切にDIDを用いることで、介入の効果をより正確に把握することができ、ビジネスの意思決定の質を高めることが可能になります。
本記事がDIDの特性や注意点を踏まえた、一歩深い分析の役に立てれば幸いです。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。差分の差分法(DID)をはじめ、因果推論による分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
こちらもご覧ください