決定木分析（デシジョンツリー）とは？ビジネス活用や注意点を解説

2023年7月31日2024年1月5日

「決定木分析（デシジョンツリー）」とは、使用できるデータの柔軟性や結果の見やすさから、多くのビジネスシーンで活用されてきた分析手法のひとつです。

本記事では、この決定木分析の考え方やビジネスシーンでの活用方法についてわかりやすく解説いたします。

決定木分析（ディシジョンツリー）とは？

決定木分析（デシジョンツリー）とは、ビジネス現場で使用しやすいといわれている分析手法のひとつです。なぜビジネスの現場で使用しやすいのでしょうか。そのひとつの答えとして『ルールを可視化しやすいこと』があります。下のグラフをご覧ください。

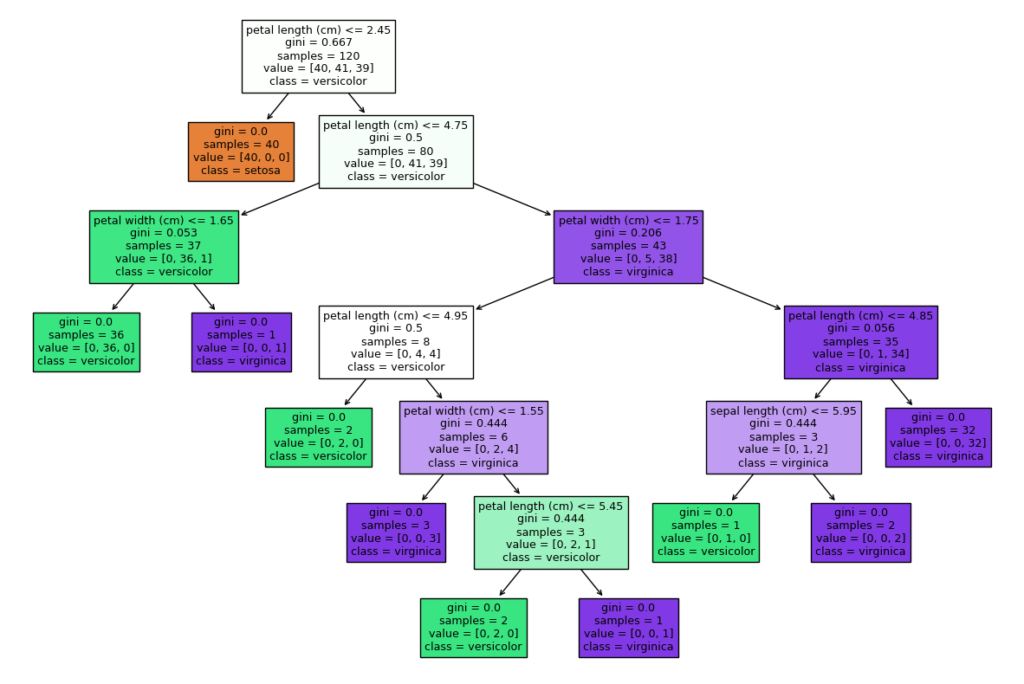
上記の決定木を用いて、決定木分析はおこなわれます。予測されるデータは、上から条件式を満たすか満たさないかで決定木を下へ進み、判別がされます。

決定木分析は一番上にあるボックスから、データの値に従って振り分ける形で判別が行われます。この可視化を具体的に説明すると、ボックス内一番上の「petal length(cm) <= 2.45」を閾値として判別が行われ、これが下に続く限りおこなわれます。データが条件をクリアする「真」の場合、左下のボックスに進みます。一方、条件に一致しない「偽」の場合は、右下に進む形で判別が行われます。

一番上のボックス内2行目にある「gini = 0.667」とは「不純度」を表す評価指標で「ジニ不純度」と呼ばれます。値が小さくなるように条件を試しながら条件分岐を作ることで分析が進められます。「ジニ不純度」のほかには「交差エントロピー」や「誤り率」などの方法で決定木を作ることもできます。

分岐を進む際の条件がシンプルであり、かつ、「なぜその予測がされたのか」が非常に理解しやすいことが決定木分析の特徴といわれています。

分類木と回帰木

決定木分析には、種類やグループを分ける『分類木』と、数値を予測する『回帰木』の2種類に分類することができます。

分類木とは、予測したい対象が質的変数の場合に用いられる決定木分析のことをいいます。一方、回帰木とは、予測したい対象が量的変数の場合に用いられる決定木分析のことをいいます。

分析からわかること

分類木からは分類予測、回帰木からは数値予測をおこなうことができます。また決定木を可視化することで、何をもってその予測がなされているのか知ることができます。

つまり、決定木分析をおこなうことで、例えば「売上予測（回帰木）」や「解約顧客（分類木）」を予測することができます。「解約顧客」の決定木を可視化することでどの説明変数が解約の要因となっていて、どの説明変数が解約の要因になっていないのかを表すことができます。

決定木分析はなぜその予測がされるのかが分かりやすいため、ビジネス上の仮説やドメイン知識と比較してデータ上で何が起こっているか、議論しやすいことが特徴として挙げられます。

また、決定木分析の発展的な手法として、「ランダムフォレスト」や「勾配ブースティング決定木」などがあります。これらは決定木分析よりも一般的に高い予測精度を出すことができるといわれています。しかし、その解釈は決定木分析よりも難しくなりますので、活用には注意が必要です。

必要なデータ

決定木分析では数値化されたデータに加え、「性別」「居住地」「既婚・未婚」などの質的変数も扱うことができます。

これらはすべて、「条件に合致しているかどうか」を決定木の判断基準としていることが理由です。量的変数の場合は大小を比較することで判断し、質的変数の場合は一致しているか否かを判断しているからです。

ただし、決定木分析は、いわゆる「教師あり学習」といわれ、事実として観測されたデータが必要になります。つまり、分類木ならすでに分類されたデータが必要であり、回帰木なら実際に観測されている数値のデータが必要になります。

また、欠損値や外れ値にも比較的強い手法となります。標準化（平均を0、分散を1とする前処理）なども不要となるため、前処理作業を削減することができます。このことから、ビジネスの現場でも扱いやすい手法となります。

決定木分析（デシジョンツリー）のビジネスシーン活用

続いては、ビジネスシーンでの具体的な活用イメージについて紹介いたします。

サービスの解約予測

サブスクリプションサービスの解約予測を例に解説いたします。

決定木分析を用いて解約に至る傾向のある顧客を特定することに加え、決定木の情報から解約に至る要因を探ることをサービスの解約を減らす取り組みとしておこないました。

まずは、必要なデータを集めます。会員顧客のサービス利用データと会員属性情報を取得します。サービス利用データと会員情報のデータを結合して決定木分析に使用します。

会員ID	性別	年代	決済	家族プラン	直近利用	月平均利用日数	解約
000AAA01	男	20代	クレジットカード	なし	1日前	20日	なし
000AAA10	男	30代	キャリア決済	なし	1日前	25日	なし
000BBB21	女	20代	キャリア決済	なし	4日前	5日	あり
000BBB31	男	40代	口座引き落とし	あり	2日前	13日	なし
000CCC01	女	30代	口座引き落とし	あり	4日前	5日	なし
000DDD02	男	50代	クレジットカード	なし	1日前	20日	なし
000ZZZ11	無回答	20代	クレジットカード	なし	2日前	20日	なし
111ZZZ11	女	20代	口座引き落とし	なし	3日前	4日	なし
…	…	…	…	…	…	…	…

上記のデータに対し、例えば以下のような決定木分析がなされたとします。

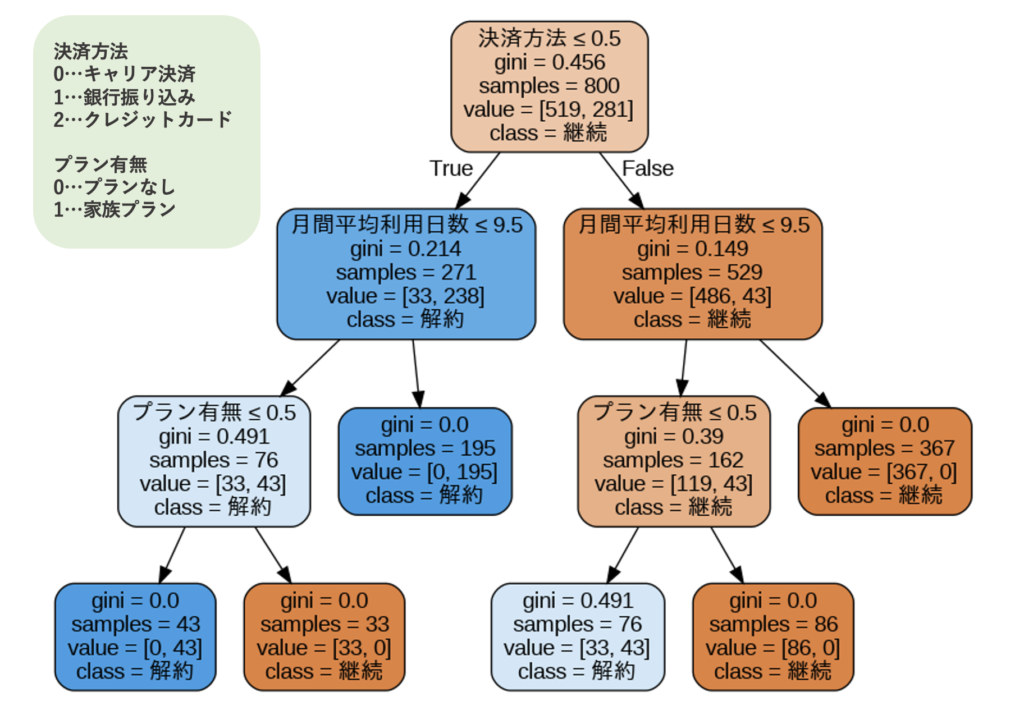
このような結果になった場合、「キャリア決済による支払いをしていて、月の平均利用日数が9.5日以下で、家族プランに入っていない」ユーザーに解約の傾向があるようです。

家族プランに入っていないということは単身者である可能性が高いと考えられます。そこで、家族の定義を広げて同居していない親や祖父母なども対象に含めることができれば解約しにくくなるのではないか？といった対策を考えることができます。

さらに、この決定木を用いることで、未知のデータに対して解約の予測をおこなうこともできます。

このようにして、決定木分析は予測とその予測に至る要因を明確にすることができます。上記の例に限らず、「購買の有無」やアンケートデータを利用した「自社商品への関心」などに活用することもできます。

その他の活用事例

サービスの解約予測のほかに、以下のような事例があります。

アンケート分析
顧客分析
自社サービス分析

アンケート分析

顧客に対しておこなったアンケートを決定木分析することで、顧客満足度に影響を及ぼしている要因を予測することができます。ただし、アンケートは一般的に「アンケート回答者である」というバイアスを含むことに注意が必要です。
満足度を目的変数とし、アンケートの回答や回答者情報を説明変数とすることで、どのような要素や属性が満足度に寄与しているのかを分析することができます。

顧客分析

決定木分析は購買の有無などを目的変数とすることで、顧客の分析をおこなうことにも適しています。
購買の有無を目的変数として、顧客の購買履歴や来店情報、ポイントサービスの活用状況などを説明変数とすることで、どういった要因が購買につながりやすいかを分析することができたり、実際に購買が発生するか否かなどを予測することができます。

自社サービス分析

自社サービスの会員情報を用いて決定木分析をおこなうことで、属性情報に限らないセグメントを見つけることができます。
自社サービスの種類を目的変数とし、自社サービスの利用履歴や継続状況、会員の属性情報などを説明変数として決定木分析をすることで、会員が利用しているサービスの種類の分類に寄与する要素を分析することができます。仮説に基づいた属性の分けられ方ができているかや、利用履歴や頻度による閾値などを見つけることができるかもしれません。

決定木分析の注意点

最後に決定木分析（デシジョンツリー）における注意点を紹介します。

適切な深さを設定する必要がある

決定木分析をおこなう際に注意しなければならないこととして、「適切な深さの設定」があります。決定木の深さとは、決定木をどれだけ複雑にするかを意味しています。深さを深くすればするほど（≒決定木を複雑にする）予測の精度は一般的に向上します。しかし、それでは「過学習」が発生してしまう恐れがあります。

過学習が発生すると、本質的でないデータの誤差にまで適合してしまい、未知のデータに対する予測精度が下がってしまうことがあります。すると、その決定木を使っていくことが難しくなってしまいます。

そうならないために、決定木分析においては、適切な深さを設定する必要があるのです。
しかし「適切な深さ」は一概には言えず、小さい数値から深くしたり、その結果をうまく解釈できるかどうかや、予測の精度、そしてこれまでの事例や研究などから探っていくことが重要です。

決定木分析は非線形の予測である

決定木分析では、ひとつの説明変数に対して条件の真偽から判別をしていきます。また、決定木の深さが2以上となると、決定木分析は非線形の予測となります。

決定木の深さが浅いと図1のように荒い予測となり精度が出にくくなります。一方で、深さを深くしていくと図4のように細かい予測となり、非線形の特性を生かして学習データに対し精度が上がる傾向にありますが、それゆえに学習データに適合しすぎる結果となり、未知のデータに対して過学習をおこしてしまう恐れがあります。

決定木の深さと非線形予測の関係性を見ると以下のようになります。

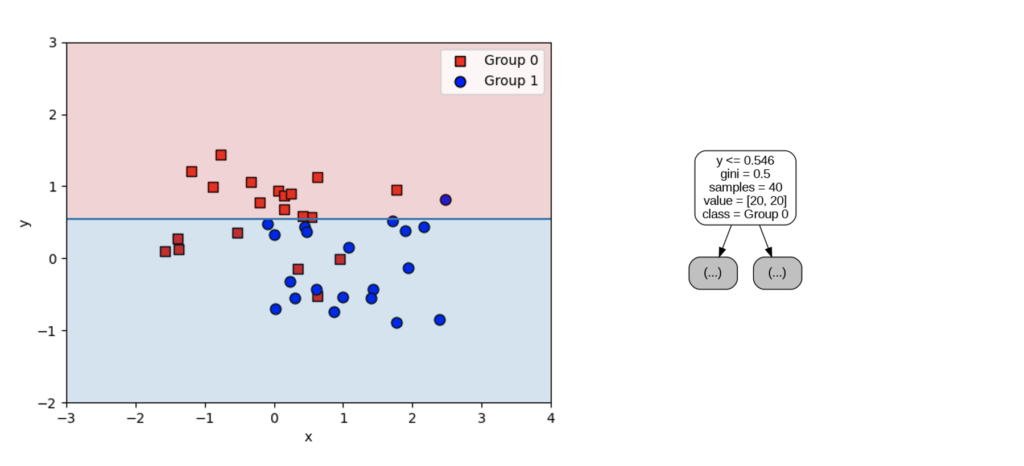
上記の散布図は、決定木の深さを1としたときの予測を平面上であらわしたものになります。次に深さを2とすると以下のような可視化になります。

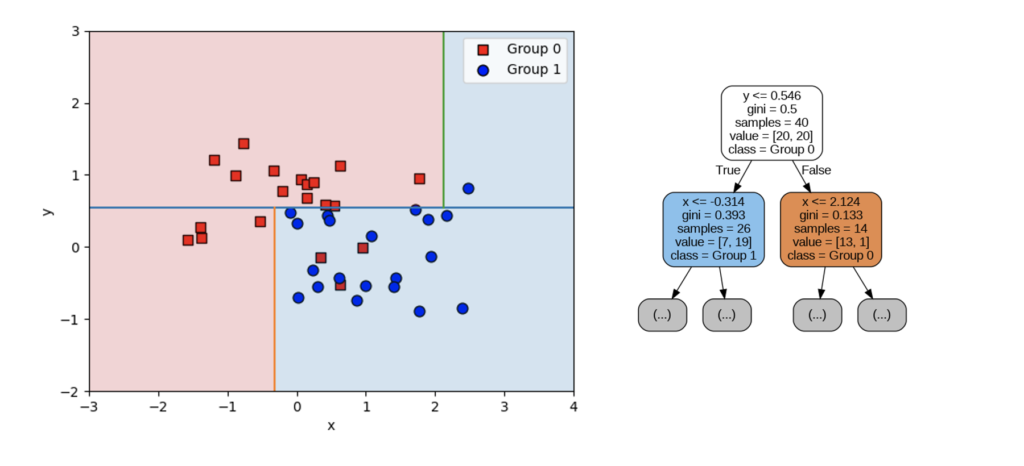
深さが2となることで、一つ目の条件（y <= 0.546）の「真」「偽」（グラフの上下半分）からさらに条件が設けられ、平面は4つに分割されています。このとき「真→真」「偽→真」「偽→真」のパターンは「ジニ不純度が0」となり、分類が完了しています。最後に「真→偽」と分けられたパターンでは、まだ分類できていないサンプルが残ってしまっています。

さらに決定木を深くします。

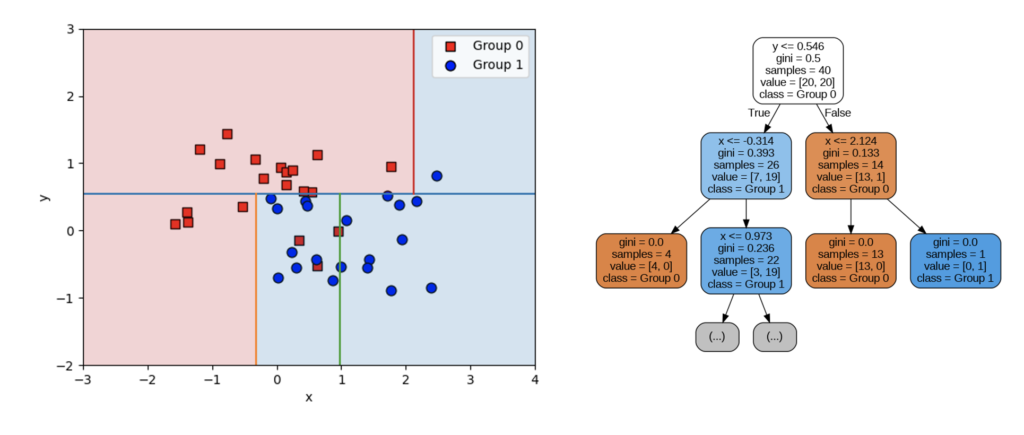
すると平面上には、Group0の分類をすべて含む形で、新たに「x<=0.973」という条件が追加されました。この条件に対して「偽」となる分類はすべてGroup1に分類ができました。さらに深さを深くすると以下のようになります。

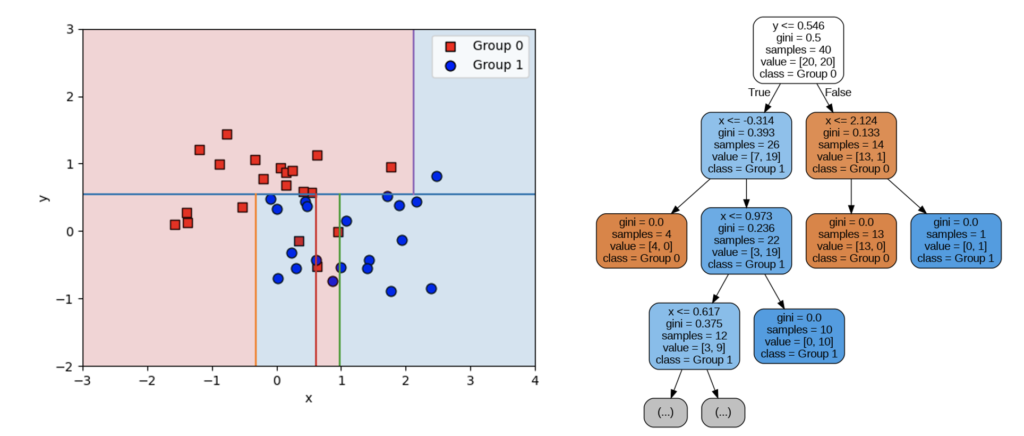
より詳しく分類することができましたが、この分類面に意味があるかどうかは、データの背景に潜む情報やビジネスドメインの知見などを活用して判断する必要があります。

まとめ

今回は決定木分析（デシジョンツリー）について解説いたしました。

決定木分析は、分類木と回帰木の2種類があり、量的変数と質的変数の両方を目的変数として適用することができます。また、前処理の制約が少ない手法でもあります。加えて、決定木を用いて、予測ルールの可視化がしやすいことも特徴のひとつです。
このことから、使い勝手の良い分析手法として、多くのビジネス現場で活用がされております。

決定木分析における注意点を踏まえた、一歩深い分析の役に立てれば幸いです。

お気軽にご相談ください！

当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。決定木分析によるモデル構築や活用の実績もございますのでお気軽にご相談ください。

データアナリティクスラボに相談する