お気軽にお問い合わせください
時系列データに対する相関分析を解説!ラグやトレンドを踏まえた相関の捉え方

時系列データに対する相関分析
相関分析は、2つのデータの関連性を数値(相関係数)で表すことで、データの特徴や傾向を把握するために広く使われる手法です。
例えば「広告費と売上」「気温と来店数」といった関係を調べることで、片方の値の動きがもう片方の値にどの程度影響しているかを確認することができます。
相関係数は -1 から 1 の範囲を取り、±1 に近いほど強い相関、0 に近いほど相関がみられないことを意味します。
ただし、相関分析はシンプルで便利な分析手法である一方、時間の流れを持つデータ(時系列データ)にそのまま適用すると、データの関連性を正しく評価できない場合があります。
その主な原因は、「トレンドや季節性による疑似相関」と、「効果が遅れて表れる時間差(ラグ)」です。
こうした点を踏まえて活用すべきであるのが、自己相関や相互相関といった「時系列データならではの相関分析手法」です。
- トレンドや季節性による疑似相関
時系列データには、長期的な増減傾向(トレンド)や季節的なパターン(夏にアイスが売れる、年末に消費が増えるなど)が含まれます。
これらを考慮せずに相関を調べると、本当は関係がないのに「強い相関があるように見えてしまう」ことがあります。
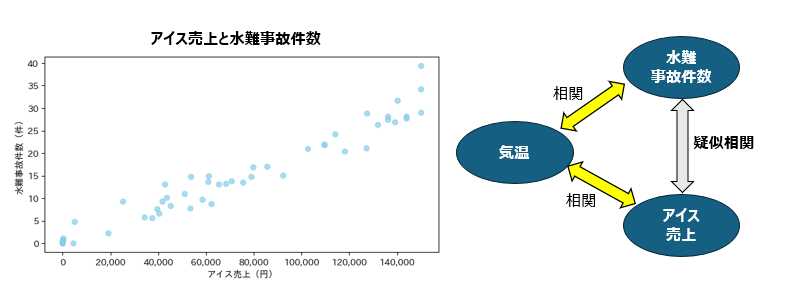
例えば、「アイスの売上」と「水難事故件数」は、どちらも「気温」が上がる夏に増加するため、見かけ上は相関関係があるように見えます。
しかし実際には、どちらも「気温」という共通の季節要因に影響を受けているだけで、アイスの売上が水難事故を増やしているわけではありません。
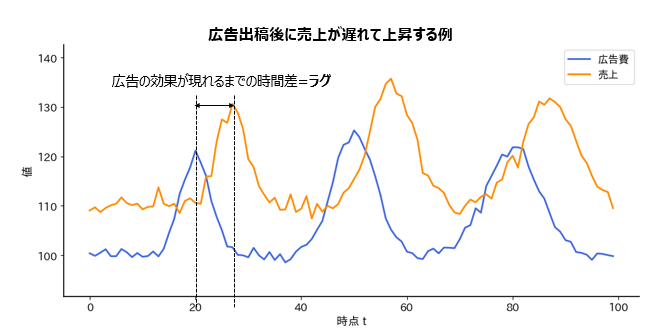
- 効果が遅れて表れる時間差(ラグ)
ビジネスの施策は、その日の数字にすぐ反映されるとは限りません。
例えば広告の場合、テレビCMを見た人がすぐ購入するとは限らず、数日後にECサイトで調べてから買うケースや、口コミや認知が広がって数週間後に売上へつながるケースもあります。
ところが通常の相関分析では「同じ日の数値同士」しか比較しません。
そのため実際には強い効果があっても、効果が小さい・関係が弱いと誤って判断してしまう危険があります。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。相関分析や時系列分析をはじめとしたデータ分析の実績も多数ございますので、お気軽にご相談ください。
ご相談・お問い合わせはこちらから
時系列データに対する相関分析の手法
以下は時系列データ特有の相関分析手法をまとめたものです。
| 分析手法 | 相関係数の種類 | 分析概要 | 相関係数の範囲 | 現場の使用頻度 |
|---|---|---|---|---|
| トレンド・季節性調整後の相関分析 | ピアソンの 積率相関係数 | トレンドや季節性を除去したデータで相関を算出し、疑似相関を回避する | -1~1 | ★★★★ (使用頻度は非常に高い) |
| 自己相関分析 | 自己相関係数 | 1つの時系列が過去の自分とどれくらい似ているかを調べ、周期性やパターンを確認する | -1~1 | ★★★★ (使用頻度は非常に高い) |
| 偏自己相関分析 | 偏自己相関係数 | 間接的な影響を除き、純粋なラグ\(k\)の影響を測定する | -1~1 | ★★★☆ (使用頻度は高い) |
| 相互相関分析 | 相互相関係数 | 2つの時系列のタイムラグ関係を調べ、先行・遅行関係を把握する | -1~1 | ★★★☆ (使用頻度は高い) |
| ローリング相関分析 | ピアソンの 積率相関係数 | 一定期間ごとに相関を計算し、時間とともに関係性が変化する様子を捉える | -1~1 | ★★☆☆ (限定的) |
トレンド・季節性調整後の相関分析
時系列データには「トレンド(長期的な増減傾向)」や「季節性(周期的なパターン)」が含まれることが多いです。そのため、そのまま相関分析を行うと、「疑似相関」と呼ばれる誤った関係性が算出されやすくなります。これは、共通のトレンドや季節要因に引っ張られて、実際には関係がなくても高い相関が得られてしまう現象です。
この問題を避けるためには、分析前に「階差を取ってトレンドを除去する」「季節分解を行う」といった前処理を施し、そのうえで相関係数を計算することが重要です。
トレンドや季節性を取り除くには、いくつかの代表的な方法があります。分析目的やデータの特徴に応じて、次のような手順を選択します。
- ①階差を取る
-
最も基本的な方法は、前期との階差(1次階差)を取ることでトレンドを除去する手法です。
式で表すと次のようになります。$$y’_t=y_t-y_{t-1}$$
また、季節性がある場合には、一定周期(たとえば12ヶ月周期)ごとの階差を取る「季節階差」も有効です。
$$y’_t=y_t-y_{t-12}$$
- ➁移動平均やローカル回帰によるトレンド除去
-
一定期間の平均値(移動平均)や滑らかな曲線(ローカル回帰)を用いて、トレンド成分を推定し、それを元の系列から差し引くことでトレンドの影響を取り除く方法です。
短期的な変動を平滑化する一方で、長期的な傾向を把握しやすくなるという特徴があります。 - ③季節分解
-
時系列データを「トレンド」「季節」「残差」の3つの成分に分ける手法です。
それぞれの要素を分離したうえで、トレンドや季節性を取り除いた残差部分を分析に用いることで、季節的な変動に影響されない関係性を評価できます。
加法モデルでは、データを以下のように表します。$$Y_t=T_t+S_t+e_t$$
ここで、\(T_t\) はトレンド成分、\(S_t\) は季節成分、\(e_t\) は残差です。
残差 \(e_t\) を相関分析に用いることで、真の関係性をより正確に把握できます。なお、データの変動幅が水準に比例して変化する場合(例:売上が大きい月ほど季節変動も大きいなど)は、乗法モデルが用いられることもあります。
$$Y_t=T_t×S_t×e_t$$ - ④回帰モデルによる調整
-
トレンドや季節性を説明変数として回帰モデルを構築し、その残差を用いて分析する方法もあります。
線形回帰や時系列モデル、あるいは季節性を明示的に扱うモデル(例:Prophetなど)を用いることで、複雑な形状のトレンドや季節性も適切に調整可能です。
自己相関分析
自己相関分析は、1つの時系列データが「過去の自分自身」とどの程度似ているかを調べる方法です。
例えば「今日の売上と昨日の売上」や「今週のアクセス数と1週間前のアクセス数」がどのくらい似た動きをしているかを確認できます。
この関係の強さを数値で表したものが 自己相関係数 で、次の式で定義されます。
$$r_k = \frac{\sum_{t=k+1}^{N} (x_t – \bar{x})(x_{t-k} – \bar{x})}{\sum_{t=1}^{N} (x_t – \bar{x})^2}$$
ここで \(x_t\)は時刻\(t\)の値、\(k\) はラグ(ずらす時間)を表します。
ビジネスの現場では、時系列データの特徴を把握するために活用されます。
よく用いられる可視化方法に、ラグごとの自己相関係数をグラフ化したコレログラム(ACFプロット)があります。
これを見ると、「どのラグで相関が強いか」「周期性があるか」を直感的に確認できます。
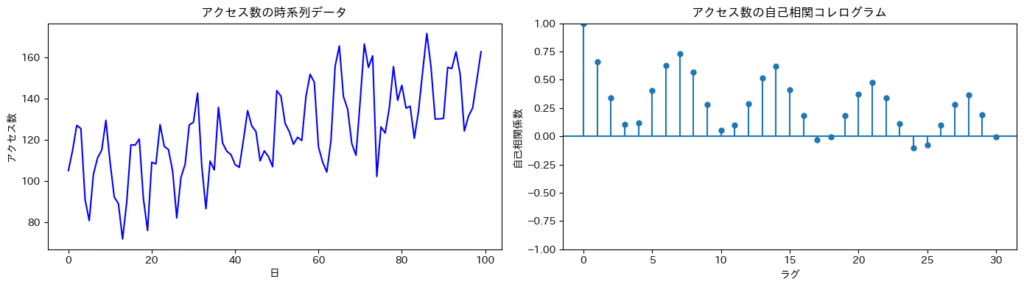
下図は、あるWebサイトの「アクセス数」に対する自己相関分析の例です。
左のグラフは元の時系列データ、右のグラフは各ラグの自己相関係数を示すACFプロットです。
ACFプロットでは、横軸がラグ(時間差)、縦軸が自己相関の強さを示しています。棒が上に伸びているほど、過去の値との正の相関関係が強いことを意味します。
ラグが進むにつれて相関が緩やかに減少していればトレンドの存在を、一定の間隔で周期的にスパイクが現れれば季節性の存在を示唆します。
この図では、ラグ7ごとに相関が高くなる傾向が見られることから、おおよそ7日周期(週次)の自己相関があると考えられます。
さらに、予測モデルを作る前の段階でも重要です。自己相関を調べることで「どのくらい前のデータの影響が今に残っているか」を確認でき、これはMAモデルやARIMAモデルでどの程度まで過去の情報を組み込むかを判断する際に役立ちます。
例えば、自己相関が2日前まで強く残っている場合には、「2日前までの誤差を組み込むモデル(MA(2))」を選ぶといった形で次数を設定します。
偏自己相関分析
偏自己相関は、自己相関に含まれる他の間接的な影響を取り除いた関係を調べる方法です。
例えば「今日の売上と1週間前の売上」を調べる場合、単純な自己相関では「昨日や一昨日を経由した影響」といった間接的な要素も含まれます。
売上が好調な日がしばらく続くようなケースでは、前の日の影響が次の日に少しずつ残るため、「1週間前の売上が今日に影響しているように見えても、実際はその間の数日を通じて徐々に影響が伝わっている」だけの可能性があります。
偏自己相関ではそうした間接的な影響を除外し、「1週間前の売上が今日にどれだけ直接的に影響しているか」を明らかにします。
この関係を数値で表したものが偏自己相関係数であり、自己相関係数をラグごとに並べて作った連立方程式を解くことで得られます。
$$\begin{bmatrix}
1 & \rho_1 & \rho_2 & \cdots & \rho_{k-1}\\
\rho_1 & 1 & \rho_1 & \cdots & \rho_{k-2}\\
\rho_2 & \rho_1 & 1 & \cdots & \rho_{k-3}\\
\vdots & \vdots & \vdots & \ddots & \vdots\\
\rho_{k-1} & \rho_{k-2} & \rho_{k-3} & \cdots & 1
\end{bmatrix}
\begin{bmatrix}
\phi_{k1}\\
\phi_{k2}\\
\phi_{k3}\\
\vdots\\
\phi_{kk}
\end{bmatrix}
=
\begin{bmatrix}
\rho_1\\
\rho_2\\
\rho_3\\
\vdots\\
\rho_k
\end{bmatrix}$$
ここで、\(\rho_i\) はラグ\(i\)の自己相関係数、\(\phi_{kk}\) がラグ\(k\)における偏自己相関係数を表します。
偏自己相関をラグごとに並べたコレログラムは PACFプロットと呼ばれ、「どのラグが直接的に効いているか」を視覚的に把握できます。
これは特にARモデル(自己回帰モデル)やARIMAモデル の設計において重要です。PACFを確認することで「過去のどの時点までを説明変数に組み込むべきか(次数p)」を判断できます。
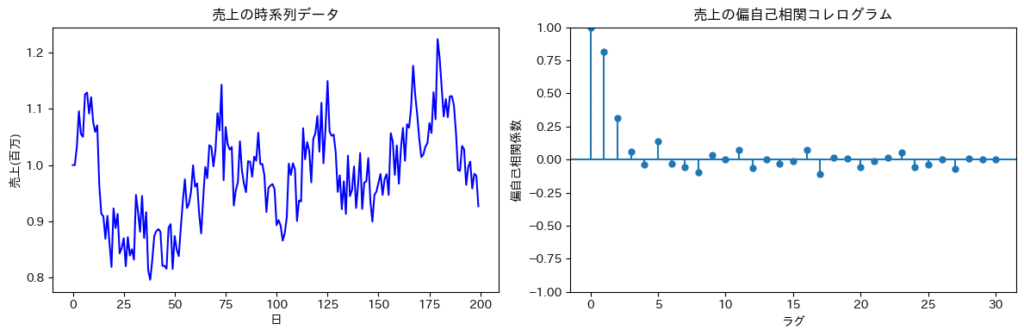
下の図では、ラグ1とラグ2の棒が高く、それ以降はほとんど0に近づいています。
これは、「1日前と2日前の売上が現在の売上に強く影響している」ことを意味します。
このような場合、AR(2)モデル(2次の自己回帰モデル)として、「2日前までの売上を説明変数に含める」設計が適しています。
相互相関分析
相互相関分析は、2つの時系列データが、時間的なズレ(ラグ)を考慮した際に、どの程度相関しているかを調べる方法です。
具体的には、一方のデータ(系列 \(x\))を時間的にずらしたとき(ラグ \(k\) を設定したとき)に、もう一方のデータ(系列 \(y\))との相関係数を計算することで、どのラグにおいて最も強い相関が現れるかを分析します。
この分析により、、一方のデータがもう一方のデータに対して、どの程度の時間差をもって連動しているのか、すなわち先行・遅行の関係や影響の時間構造を把握することができます。
この関係の強さを数値で表したものが相互相関係数で、次の式で定義されます。
$$r_{xy}(k)=\frac{\sum_{t=k+1}^{N} (x_t – \bar{x})(y_{t-k} – \bar{y})}{\sqrt{\sum_{t=1}^{N}(x_t – \bar{x})^2 \cdot \sum_{t=1}^{N} (y_t – \bar{y})^2}}$$
ここで、\(x_t\) は系列 \(x\)、\(y_t\) は系列 \(y\)、\(\bar{x}, \bar{y}\) はそれぞれの平均値、そして \(k\) はラグ(時間のずれ)を表します。
相互相関係数をラグごとに並べたコレログラムがCCFプロット であり、「どちらのデータが先行して動き、どちらが遅れて反応しているか」を直感的に確認できます。
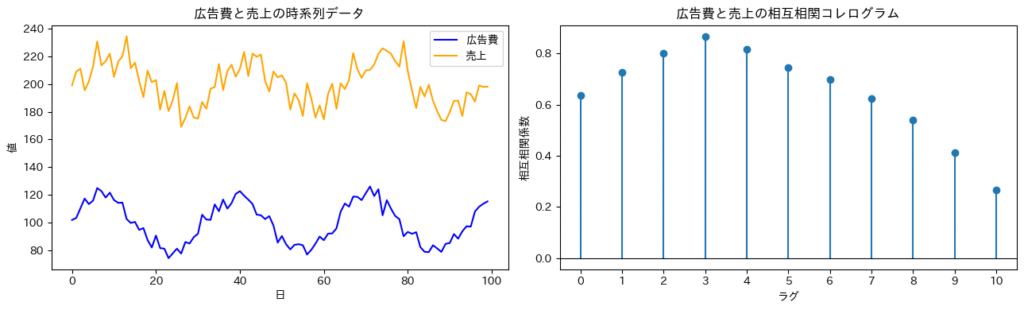
例えば「広告費と売上の関係」を分析する場合、CCFを確認すれば、
「広告出稿の効果が3日後に現れる」「キャンペーン終了後、1週間ほどで効果が薄れる」といった効果のタイムラグを把握することができます。
これにより、広告予算の投下タイミングの最適化や、販促施策の効果持続期間の見極めが可能になります。
下の図では、CCFプロットにおいてラグ3で相関が最大となっているため、「広告出稿の効果が3日後に最も強く表れる」ことがわかります。
ローリング相関分析
ローリング相関分析は、一定の期間(移動ウィンドウ)ごとに相関係数を算出し、その推移を観察することで、2つのデータ間の関係性が時間とともにどのように変化しているかを把握する手法です。
この分析の目的は、データ全体を通じた一括の相関を見るのではなく、相関の強さや向きが、期間ごとにどのように変動しているかという「関係性の推移」に着目する点にあります。
移動ウィンドウとは、「直近30日」や「直近8週間」などの一定の期間を指し、ローリング相関分析では、このウィンドウを順次ずらしながら相関を計算していきます。
こうして得られた相関係数を時系列上に並べたものがローリング相関プロットであり、相関の強弱や正負の変化が、どの時期に生じているのかを視覚的に確認することができます。
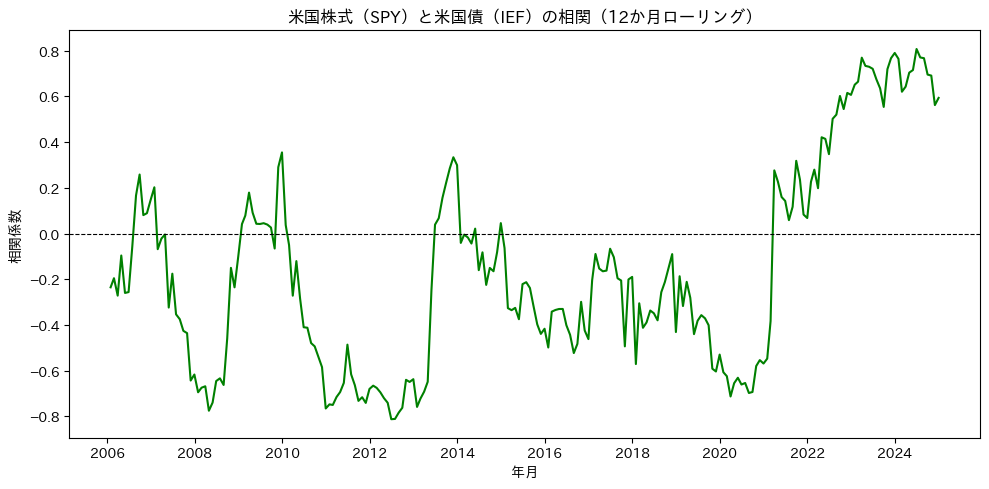
例えば「株式と債券のリターン」の関係を分析する場合、一般的には株価が上昇すると債券価格は下落するという負の相関が見られます。これは、景気拡大局面では株価が上がりやすく、同時に金利上昇によって債券価格が下がるという典型的なパターンによるものです。
一方で、景気後退や金融危機などの不確実性が高い局面では、投資家がリスク資産を同時に手放す傾向が強まり、株式と債券がともに下落する、つまり相関が一時的に高まる現象が生じます。
このように、ローリング相関分析を使うことで、「平常時は逆相関、混乱期は正相関」といった関係性の変化を時系列で把握でき、分散投資の効果が弱まる時期を早期に見極めることが可能になります。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。相関分析や時系列分析をはじめとしたデータ分析の実績も多数ございますので、お気軽にご相談ください。
ご相談・お問い合わせはこちらから
時系列データに対する相関分析からわかること
相関係数による客観的評価
相関係数は、2つの変数間の関連性の強さと方向性を、-1〜+1の数値で表す客観的な指標です。
これにより、変数同士の関係を感覚ではなく、数値として比較・評価できます。
時系列データの分析においては、広告費と売上のように時間の流れに沿った指標同士の相関を算出することで、どの指標が比較的強く結びついているかを明確にできます。
ただし、相関の強さの判断基準は分析の分野やドメインによって異なるため、単独の値だけで解釈するのではなく、複数の候補変数を並べて相対的に比較することが重要です。これにより、予測モデルや施策評価において優先的に検討すべき変数を選定するための根拠となります。
時系列データにおける時間的な関係性の特徴
時系列データの相関分析では、単に「2つの変数が関連しているか」を確認するだけでなく、その関係がどのような時間的特徴を持つのかを多角的に把握することが重要です。
具体的には、効果が時間差を伴って現れるのか(ラグ)、周期的なパターンが存在するのか(周期性)、関係性が時間とともに変化するのか(持続性・変動)といった観点から分析を行うことで、より実態に即した理解が得られます。
- タイムラグの把握
-
2つの時系列変数の関係が時間差を伴って現れるかを相互相関分析によって確認できます。
例えば広告費と売上の関係では、広告出稿後すぐに反応が出るとは限らず、数日〜数週間遅れて効果が表れる場合があります。このようなラグを把握することは、広告効果の正確な評価やマーケティング施策の最適なタイミング設計に役立ちます。また、予測モデル構築時に有効なラグを特定する手がかりにもなります。
- 周期性や繰り返しパターン
-
1つの系列内での繰り返しや周期的な動きを自己相関分析によって確認できます。
例えば、販売個数の時系列データに自己相関を適用することで、毎週・毎月の周期的な動きを把握することが可能です。こうした周期性の把握は需要予測や在庫管理に役立ちます。
また、時系列モデルの構築においても重要な基礎情報となります。特に、ARIMAやSARIMAといったモデルでは自己相関や偏自己相関の結果を基にラグの次数や季節成分を設定する際の参考として活用されます。 - 関係の持続性・変化の把握
-
2つの変数の関係が一時的なものか、長期的に持続しているものかをローリング相関分析によって可視化できます。
例えば、キャンペーンと売上の関係を見た場合、キャンペーン直後にだけ強い相関が現れることもあれば、その効果が数ヶ月持続することもあります。為替と株価のように普段は強い関係を持つ指標でも、金融危機や政策発表といった特定のイベントを契機として、相関が急激に変化するケースもあります。このように、ローリング相関は関係性の持続性や変動を把握するための有効な手法となります。
ビジネス活用例
活用事例①:KGIの先行指標抽出と構造検証
ビジネスにおいて、売上のようなKGIに影響を与える要因を特定するには、相関分析、主成分分析、回帰分析などの統計手法を組み合わせることが有効です。相関分析では、各指標間の関係性を把握し、どの変数がKGIと強く関連しているかを確認できます。これは、回帰分析や構造方程式モデリング(SEM)で使用する説明変数を選定する際の参考になります。
これらの分析を段階的に行うことで、KGIに影響を及ぼす主要な要因やその構造的な関係を把握し、最終的にはSEMを用いて因果構造を検証することも可能です。
以下では、その一連の流れを具体的な活用例とともに解説します。
データの収集・整形のフェーズでは各媒体からデータを取得し、欠損値の処理やデータの粒度の統一などの前処理を行い、分析に適した形式に整えます。
このステップで整形を行った後のデータ例は以下の通りです。
| 日付 | 売上(円) | 認知率(%) | 購入意向率(%) | TV広告費(円) | ・・・ |
|---|---|---|---|---|---|
| 2023-04-01 | 45,057,184 | 75.20 | 53.42 | 1,253,000 | ・・・ |
| 2023-05-01 | 44,598,355 | 84.09 | 55.39 | 1,615,000 | ・・・ |
| 2023-06-01 | 40,757,633 | 89.28 | 55.69 | 1,453,000 | ・・・ |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
整形したデータを基に、主要な指標の推移や関係性を可視化し、全体像を把握します。
まず、売上・認知率・広告費といった主要指標の分布やトレンドを確認し、データの特徴や季節性、異常値の有無を整理します。
この段階では、単純な値の大小や増減だけでなく、時系列的な変動パターンや各指標間の動きの類似性にも着目します。
こうした基礎分析により、データの信頼性や特性を理解し、後続の相関分析やSEMによる構造検証に向けた前提を整えます。
続いて、相関分析を通じて、どの指標が売上や認知率と強く結びついているかを探索します。
このとき、同時点での関係性(単純相関)に加えて、時間差を考慮した相互相関も確認します。
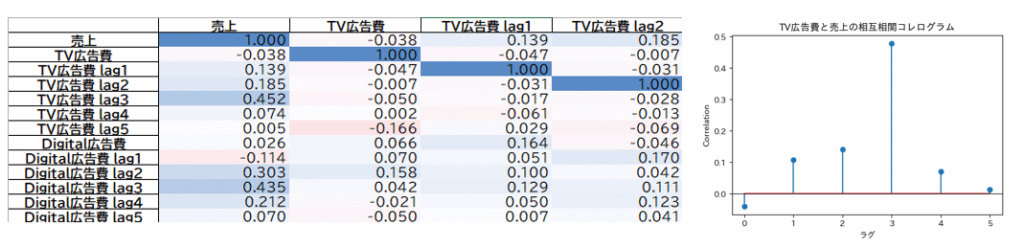
単純相関では、指標間の関係性をヒートマップ(相関行列)で可視化し、全体的な傾向を把握します。
一方、相互相関では、KGI(例:売上)と各指標の関係に加えて、指標同士の時間的な関係性も確認します。
これらをラグごとのヒートマップやコレログラムで可視化することで、指標間に存在するタイムラグや先行・遅行の関係といった、時間的な構造を把握できます。
また、変数同士の相関が高すぎないか(多重共線性)を確認することも重要です。
多重共線性があると、SEMや回帰分析を実施する際に各変数の影響を正しく分離できず、推定結果が不安定になる可能性があります。
必要に応じて、似た傾向を持つ変数を統合したり、不要な変数を除外したりして整理します。
相関分析の結果やドメイン知識を基に、SEMに使用する変数を選定し、想定される因果関係を矢印で示したパス図を設定してモデルを構築します。
パス図は仮説構造に基づいて初期設計を行い、その後、適合度指標を確認しながら微調整を加えていきます。
モデル選定の際には、基本的には適合度指標を比較し、より適合度の高いモデルを採用します。
ただし、ドメイン知識が十分にあり、複数モデルの指標に大きな差が見られない場合には、
ビジネス上の妥当性や現場感覚を重視して、最も現実的なパス構造を持つモデルを選択することもあります。
今回は、適合度指標のAGFIが最も高かったモデルを最終モデルとして採用しています。
下図は、最終的に選定したパス図です。
※パス係数はすべて標準化係数を使用しています。


活用事例➁:時系列モデルのラグ数設定
自己相関はモデルの次数(ラグ数)を決定する際に重要な指標となります。自己相関を分析することで、売上が週単位や月単位などの周期性を持つかどうかを把握できます。例えば、ECサイトの売上データにおいて、前月の売上と今月の売上に強い相関が見られる場合、自己回帰モデル(ARモデル)の次数を「1か月前の売上を説明変数として組み込む」形に設定します。こうして周期性をモデルに反映させることで、需要変動をより正確に捉えられ、予測精度の向上が期待できます。その結果、キャンペーン効果の評価やリピート需要を考慮した在庫計画など、実務に結びついた意思決定に役立ちます。

当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。相関分析や時系列分析をはじめとしたデータ分析の実績も多数ございますので、お気軽にご相談ください。
ご相談・お問い合わせはこちらから
注意点
線形性の前提
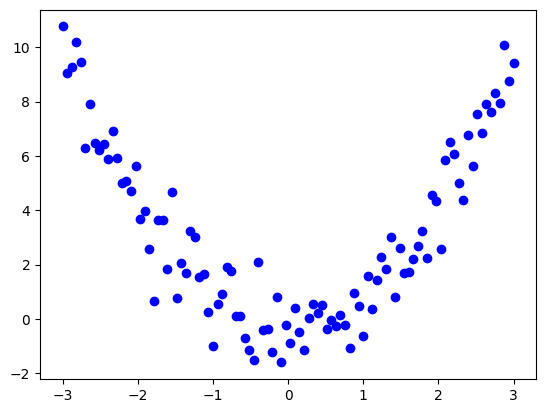
時系列データで用いられる相関分析も、ピアソンの相関係数と同様に、変数間に線形な関係があることを前提としています。非線形な関係が存在する場合、相関係数の値は実際の関係を正しく反映せず、誤解を招く結果となる可能性があります。下図の場合、曲線的な関係があるにもかかわらず、相関係数は低い値(例:-0.02)を示します。
そのため、相関を算出する前には、散布図や時系列プロットを確認し、関係が直線的であるかを見極めることが重要です。
外れ値の影響
データに外れ値がある場合、相関係数に大きな影響を与え、実際のデータ間の関係性を過大評価または過小評価する原因となります。特に時系列では、キャンペーン・システム障害・天候などによる一時的な異常値や突発的なイベントが発生しやすく、これらが相関を歪めることがあります。
このような場合には、外れ値を削除するか、外れ値の影響を考慮したうえで分析を進めることが重要です。
正規分布の仮定
相関分析は、データが正規分布に従う場合に最も信頼性が高いです。データが偏っている場合には、結果が歪む可能性があります。このような場合には、以下のような方法でデータの偏りを軽減することが推奨されます。
- 1. 対数変換
-
正の値を持つデータが右に大きく偏っている(裾が長い)場合に特に有効です。大きな値を相対的に圧縮することで、分布の歪みを緩和し、正規分布の形状に近づけることができます。
- 2. Box-Cox変換
-
データの偏りを解消するために、最適な変換パラメータ \(\lambda\) をデータから推定する手法です。対数変換は \(\lambda=0\) の場合に相当しますが、Box-Cox変換は \(\lambda\) の値をデータに合わせて連続的に微調整できるため、対数変換のような固定された変換を適用するよりも柔軟に、分布を正規分布の形状に近づけることができます。
ただし、変換式の性質上、正の値のみを持つデータに適用可能です。 - 3. Yeo-Johnson変換
-
Box-Cox変換の拡張手法であり、正の値だけでなく負の値を含むデータにも適用できる点が特徴です。Box-Cox変換と同様に、データから最適な変換パラメータを推定する手法です。
サンプルサイズとデータ粒度
サンプルサイズが小さいと、ランダムな変動や外れ値の影響を受けやすく、相関係数が実際の関係を正しく反映しないことがあります。
例えば、日次データで1年分(約365点)であれば、一時的なノイズや外れ値があっても全体の傾向に大きな影響はありません。しかし、月次データで1年分(12点)の場合は、たった1点の異常値や一時的な変動で相関が大きく歪むことがあります。さらに、サンプル数が少ないと、トレンドや周期の影響を十分に分離できないこともあります。そのため、相関を安定的に評価するには、十分な期間のデータ(季節要因がある場合は2〜3周期分など)を確保することが重要です。
データの粒度も評価の安定性に影響します。月次より週次、週次より日次とすることで、より多くのサンプルを得られ、相関係数の信頼性が高まります。
ただし、一度月次データとして集めてしまうと、週次や日次といった細かい粒度に戻すことはできません。週次のデータを月次・年次に変換することは可能ですが、その逆はできないため、分析目的に応じて適切な粒度でデータを収集することが重要です。
定常性の確認
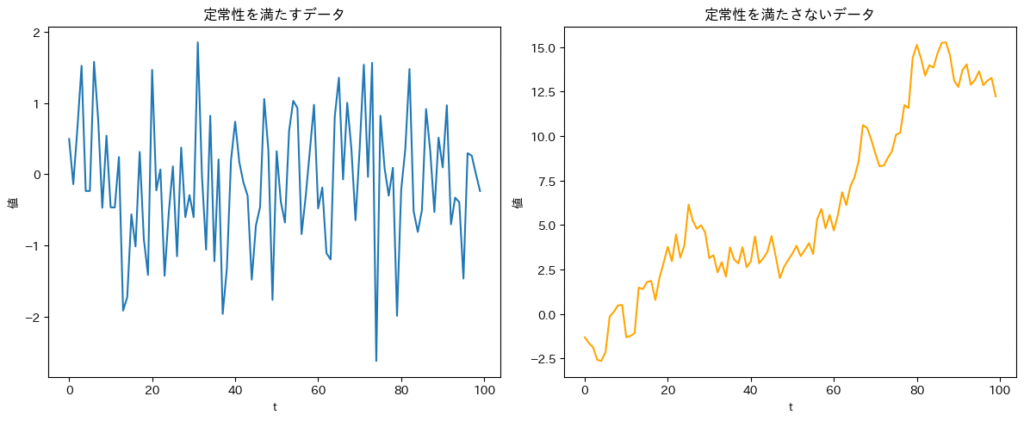
時系列分析では、データの「定常性」が非常に重要になります。
「定常性」とは、時系列データの平均や分散といった統計的な性質が、時間の経過によらず一定である状態を指します。一方、時系列データは、トレンドや季節性によって平均や分散が時間とともに変化する「非定常性」を持つことが多く、このまま相関分析を実施すると、疑似相関が生じる可能性があります。
そのため、相関分析を行う前には、トレンド除去や季節調整といった処理を行い、データをできるだけ定常な状態に整えてから分析を行うことが重要です。
相関係数は因果関係を示す指標ではない
相関係数が高くても、一方の変数が他方の原因であるとは限りません。
特に時系列データでは、時間の経過とともに変化する共通のトレンドや外部環境の影響によって、疑似相関が生じることがあります。
例えば、広告費と売上が同じ時期に増加している場合でも、それが必ずしも広告の効果を意味するとは限りません。
季節要因や景気動向、キャンペーン時期など、広告費と売上の両方に影響を与える第三の要因が存在する可能性があります。
したがって、相関分析をおこなう際には、因果関係を安易に推測せず、結果に影響を及ぼしていると考えられる他の要因や時間的な遅れ(ラグ)を検討することが重要です。
また、相関分析は、データの関連性を把握する初期分析として有効です。しかし、単独では因果関係の評価やより深い理解には十分ではありません。そのため、以下のように他の分析手法を併用してデータを多角的に分析し、総合的な評価を行うことが有効です。
- 回帰分析を用いて、特定の要因がどの程度結果に寄与しているかを定量的に評価する。
- 相互相関分析を用いて、どちらが先に動くか(先行・遅行関係)を確認する。
- 因果推論(DIDやグレンジャー因果性検定など)により、時間的順序を踏まえた因果性を検証する。
変数が多い場合、結果の解釈に苦労する
相関分析では、扱う変数の数が増えるほど、結果の解釈が難しくなります。
さらに、時系列データの場合は、変数の組み合わせだけでなく、時間的なずれ(ラグ)も考慮する必要があります。
同じ2つの変数でも、「同時点の相関」だけでなく、「1期前」「2期前」など、
さまざまな時間差を検討する必要があるため、分析すべき組み合わせの数が大幅に増えます。
その結果、単に変数が多いというだけでなく、時間軸を含めた多次元的な関係を読み解く必要があり、
相関の解釈は一層複雑になります。
したがって、変数が多い場合には以下のような工夫をおこなうことが重要です。
① 仮説を立てたうえで分析を行う
事前に仮説を設定することで、分析対象となる変数を絞り込まれ、重要な関係性を特定しやすくなります。
➁ 次元削減手法を活用する
必要に応じて主成分分析や因子分析などの次元削減手法を用いることで、多数の変数を少数の要因にまとめることができるため、それぞれの相関係数を確認する回数を減らすことができます。
これらの工夫を通じて、相関分析の有効性を高めることができます。
欠損値の補完
データに欠損値が存在する場合、その補完方法は相関係数の値や解釈に大きく影響を及ぼす可能性があります。
欠損値への対処法としては、欠損値を含むレコードを削除する(リストワイズ削除)、平均値や中央値で補完する、回帰補完をおこなう、多重代入法(Multiple Imputation)を適用するなど、さまざまな手法が存在します。
ただし、時系列データでは時間的な連続性があるため、
単純な平均値補完などでは時系列のパターン(トレンドや季節性)が失われるリスクがあります。
このため、時間構造を考慮した補完方法を選ぶことが重要です。
前後の値から中間値を推定する線形補間、直前や直後の値で補う前方・後方補完、
トレンドを保ちながら滑らかに補完する移動平均やローカル回帰(LOESS)などが代表的な手法です。
重要なのは、分析者が欠損値の発生メカニズムを理解し、適切な補完方法を選択することです。
分析結果を解釈する際には、どのような補完方法が用いられたのか、そしてその方法が結果に与える潜在的な影響について十分に考慮する必要があります。
可能であれば、異なる補完方法を適用し、それぞれの相関係数の変化を比較検討することで、分析結果がどの程度安定しているか(補完方法によって大きく変わらないか)を確認し、関係者間で合意することが望ましいです。
まとめ
今回は、時系列データに対する相関分析について解説しました。
相関分析は、変数間の関係性を数値で把握し、KGIに影響を与える要因の探索や仮説構築に役立つ基本的な手法です。
一方で、時系列データではトレンドや季節性による疑似相関、効果の時間差(ラグ)などを考慮しなければ、誤った結論を導く可能性があります。
自己相関や相互相関、ローリング相関といった手法を併用し、時間的な構造を踏まえて分析を行うことで、より実態に即した理解が得られます。
本稿が、時系列データにおける相関分析の理解と実践に貢献できれば幸いです。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。相関分析や時系列分析をはじめとしたデータ分析の実績も多数ございますので、お気軽にご相談ください。
ご相談・お問い合わせはこちらから
こちらもご覧ください