Index
はじめに
データソリューション事業部の関田です。
本記事では、2025年4月にarXivに投稿された CAT: Circular-Convolutional Attention for Sub-Quadratic Transformers (Yoshihiro Yamada) という論文について解説します。本論文はタイトルの通りTransformerに関連する研究で、特にAttention機構の計算量に着目しています。Transformerは昨今発展が目覚ましい大規模言語モデルの基礎をなすモデルであり、この計算量が削減可能であることは注目に値します。
※本記事では元論文と異なる定義を採用している箇所があります。具体的な表記法が異なるだけで本質的な違いはありませんが、論文と見比べられる際には注意いただくようお願いいたします。
1. 概要
従来のTransformerにおけるAttention機構は、\( \mathcal{O}(N^2)\) の計算量を要することが知られています。これでは、例えば言語モデルで長い文章を扱う際に計算量が膨大になってしまうという課題があります。この問題を解決するために様々な研究がなされ、計算量を \(\mathcal{O}(N)\) にまで落とす手法も開発されています。しかしそれらは表現力を落とす近似手法などを用いており、精度面での課題が発生していました。
本論文では Circular-convolutional ATtention (CAT) という新たな手法を提案し、表現力を欠くことなく計算量を \(\mathcal{O}(N \log N)\) に削減することに成功したことを報告しています。さらに、理論的に計算量を削減可能であるという報告だけでなく、大規模データを用いたいくつかの実験により、実用的なスケールで効果を発揮することを示しました。
2. 従来のAttention機構
本記事では詳細を省きますが、従来のAttention機構では式 \((1)\) のようにAttentionを計算します。
$$ \mathrm{Attention}(Q, K, V) = \mathrm{softmax}\biggl( \frac{QK^T}{\sqrt{d_k}} \biggr) V \tag{1} $$
ここで、 \(Q, K, V \in \mathbb{R}^{N \times D}\) はそれぞれQuery、Key、Valueと呼ばれ、長さ \(N\) 、特徴量次元 \(D\) の入力から作成される行列です。このAttentionの算出には \(\mathcal{O}(N^2)\) の計算を要します。したがって、Transformerの計算量削減のためにはこのAttention機構に工夫を加える必要があります。
3. CAT
3.1. Engineering-Isomorphic TransformerとCAT
本論文では、以下の4つの性質を持つモデルを Engineering-Isomorphic Transformer という枠組みで定義しています。CATは、ここで定義されるEngineering-Isomorphic Transformerの具体的なモデルのひとつです。
- \(\mathbf{softmax}\) 関数が使用されていること
Attention機構の核となる \(\mathrm{softmax}\) 関数を用いた構成である式 \((2)\) の形式を保持している必要があります。これにより、安定した学習が可能となります。
$$ F_{\mathrm{out}}(x) = \mathrm{softmax} (F_{\mathrm{attn}}(x))F_{\mathrm{value}}(x) \tag{2} $$
従来のAttention機構は以下の対応によりこの性質を満たします。
$$ F_{\mathrm{attn}} = \frac{QK^\mathrm{T}}{\sqrt{d_k}}, \quad F_{\mathrm{value}}=V $$ - 計算量が \(\mathcal{O}(N^2)\) より小さいこと
従来のAttention機構はこれを満たしません。 - モデルのパラメータを増やさないこと
従来のTransformerモデルと比べて、学習可能なパラメータが増えていない必要があります。 - ハイパーパラメータを増やさないこと
近似手法によっては、入力長 \(N\) に対して適切な近似を行うためのハイパーパラメータが追加され、そのチューニングが必要なことがあります。Engineering-Isomorphic Transformerは、入力長などによらず、核となる機構によって適切なスケーリングができることを要請します。
以上の性質を満たすEngineering-Isomorphic Transformerは、従来のTransformerと比べて表現力や精度を損なうことなく計算量を削減することが可能となります。Engineering-Isomorphic Transformerのひとつの具体例であるCATでは、Attentionの計算に巡回畳み込みと高速フーリエ変換を適用することで、精度を損なうことなく計算量を \(\mathcal{O}(N \log N)\) に削減しました。
3.2. CATの計算
新たなAttentionのアイデア
まずはAttention \(F_{\mathrm{cat}}\) を次のように計算することを考えます。
$$ F_{\mathrm{cat}} = \mathrm{Roll} \Bigl(\mathrm{softmax}(xW_A)\Bigr) \ (xW_V)\ \in \mathbb{R}^{N \times D} \tag{3} $$
ここで、各要素の定義は以下です。
- Rolling Operation
列ベクトル \(\textbf{z} \in \mathbb{R}^N\) に対して、 \(\mathrm{Roll}(\textbf{z}) \in \mathbb{R}^{N \times N}\) を次のように定義します。
$$ \mathrm{Roll}(\textbf{z}) = \begin{bmatrix} z_{0} & z_{N-1} & \dots & z_{1} \\ z_{1} & z_{0} & \dots & z_{2} \\ \vdots & \vdots & \ddots & \vdots \\ z_{N-1} & z_{N-2} & \dots & z_{0} \end{bmatrix} $$
この行列の2列目からN列目は、1列目のベクトルを回転させたものになっています。このような行列を巡回行列と呼びます。
- 入力と重み行列
入力を \(x \in \mathbb{R}^{N \times D}\) 、学習可能なパラメータである重み行列を \(W_A \in \mathbb{R}^{D \times 1}, W_V \in \mathbb{R}^{D \times D}\) とします。従来のTransformerではQueryとKeyに分けられていましたが、ここでは \(W_A\) でまとめて表しています。
以上の定義により、 \(F_{\mathrm{cat}}\) は \(\mathrm{Roll} \Bigl( \mathrm{softmax}(xW_A) \Bigr) \in \mathbb{R}^{N \times N}\) と \(xW_V \in \mathbb{R}^{N \times D}\) の積によって求められます。ここで、式 \((3)\) で表される機構がEngineering-Isomorphic Transformerであるか確認してみます。
- \(\mathbf{softmax}\) 関数が使用されていること
式 \((3)\) は式 \((2)\) と同じ形になっています。
※ \(\mathrm{Roll}\) 関数が外側にあることが気になる場合は、 \(F_{\mathrm{attn}}=\mathrm{Roll}(xW_A)\) に対して列方向に \(\mathrm{softmax}\) 関数を適用すると考えればよいです。 - 計算量が \(\mathcal{O}(N^2)\) より小さいこと
式 \((3)\) は \(\mathbb{R}^{N \times N} \times \mathbb{R}^{N \times D}\) の計算を行うため計算量は \(\mathcal{O}(N^2)\) となり、この条件を満たしていません。 - モデルのパラメータを増やさないこと
従来のTransformerではQueryとKeyに対してそれぞれ \(\mathbb{R}^{D \times D}\) の重み行列が必要であった一方、式 \((3)\) では \(W_A \in \mathbb{R}^{D \times 1}\) に置き換わっており、パラメータ数は削減されています。 - ハイパーパラメータを増やさないこと
ハイパーパラメータを追加することなく、Attention機構を置き換えるだけで実現可能です。
式 \((3)\) では、計算量が削減されていません。したがって、計算量に関して工夫が必要です。
計算量削減:巡回畳み込みと高速フーリエ変換
式 \((3)\) で \(\mathcal{O}(N^2)\) のままであった計算量を削減するために、高速フーリエ変換で巡回畳み込みを行います。ここで巡回畳み込みとはまさに式 \((3)\) が行っていることで、巡回行列と他の行列の積を計算することです。具体的に式 \((3)\) では、 \(xW_V * \mathrm{softmax}(xW_A)\) なる巡回畳み込みを行っています。巡回畳み込みについてより詳しい説明は付録A.1. に掲載しています。この巡回畳み込みは、高速フーリエ変換によって \(\mathcal{O}(N \log N)\) で計算できることが知られています。巡回畳み込みと高速フーリエ変換の関係については付録A.2. に掲載しています。高速フーリエ変換とその逆変換をそれぞれ \(\mathrm{FFT}, \mathrm{RFFT}\) と書くと、巡回畳み込みを行っている式 \((3)\) は以下のように高速フーリエ変換で計算することが可能です。
$$ F_{\mathrm{cat}} = \mathrm{RFFT}\Bigl( \mathrm{FFT}(\mathrm{softmax}(xW_A)) \cdot \mathrm{FFT}(xW_V) \Bigr) \tag{4} $$
これがCATで行われるAttentionの計算です。
3.3. 従来のAttentionとCATの比較
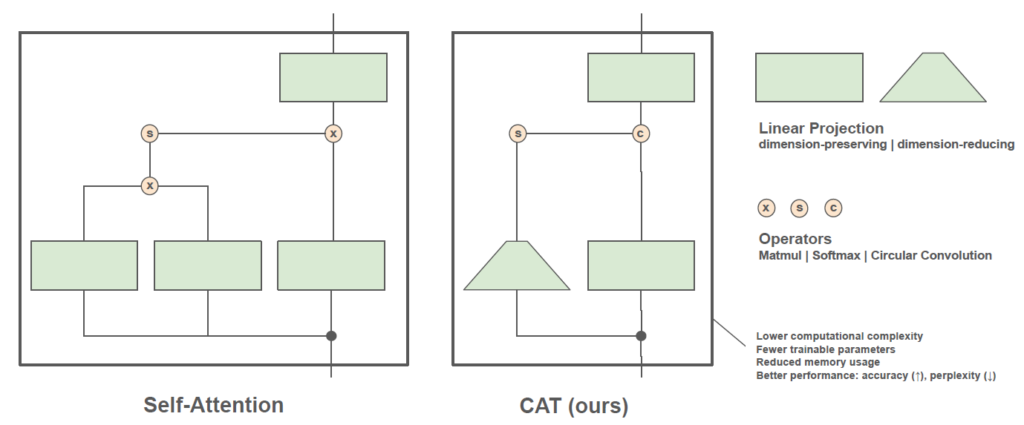
図1は従来のAttentionとCATの比較です。従来はQueryとKeyの次元を保ったまま掛けていましたが、CATではそれらをひとつの行列で表し、かつ次元も削減しています。これにより学習可能なパラメータやメモリ使用量が削減されます。一方、 \(\mathrm{softmax}\) 関数を残すことにより全トークン間の関連性を大局的に捉えることができており、精度低下を防いでいます。そして巡回畳み込みを高速フーリエ変換で実行することにより、計算量の削減にも成功しています。
4. 実験
論文では画像分類および言語モデリングを実施してCATを評価しています。ベンチマークに使用されたデータセットや元モデル、評価指標は次の通りです。
| タスク | データセット | 元モデル | 評価指標 |
|---|---|---|---|
| 画像分類 | ImageNet-1k [2] | ViT CLIP-B/L [3, 4] | 正解率 |
| 言語モデリング | WikiText-103 [5] | Transformer-XL [6] / GPT-2 small [7] | word perplexity (word PPL) |
従来のAttentionとCATの比較において、Attention機構をCATに置き換える以外の変更はありません。置き換えのパターンとしては、次の3パターンがあります。
- Attention:従来のAttention機構
- CAT:すべてのAttentionをCATに置き換えたもの
- CAT-alter:半分のAttentionをCATに置き換えたもの
その他詳細な設定は [1] の5章をご参照ください。
4.1. 画像分類
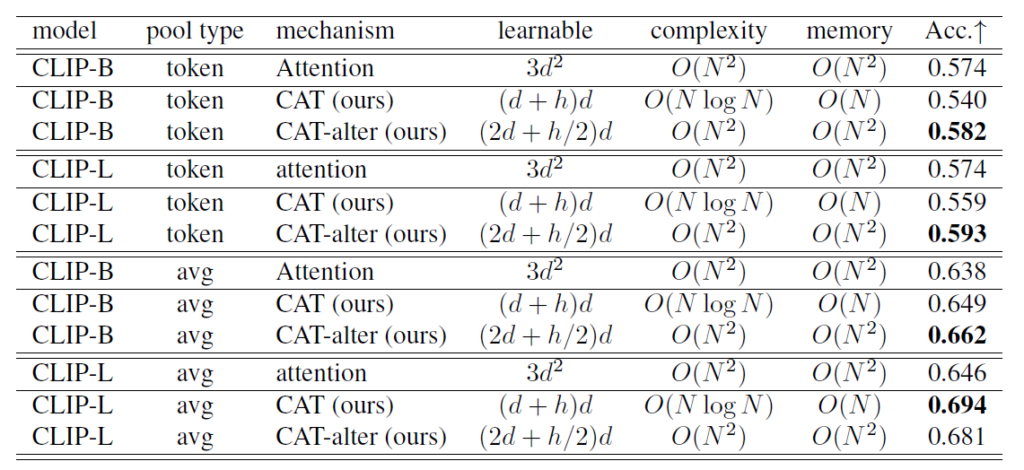
画像分類の結果は図2の通りです。図2にはモデル、プーリング方法、Attention機構、学習可能パラメータ数、計算量、メモリ使用量、正答率がまとめられています。ここで、 \(d\) は入力の次元、 \(h\) はAttention Headの数を表します。Pool TypeはToken PoolingとAvg Poolingの2種類が試されています。Token Poolingは特殊なトークンを特徴として抽出し、Avg Poolingではすべてのトークンの平均を取って特徴を抽出します。正答率を比較すると、CATはAvg Poolingでは従来のAttentionを上回っていますが、Token Poolingでは下回っています。それに対し、CAT-alterは本実験のいずれのパターンにおいても従来のAttentionの正答率を上回っています。したがって、部分的にAttentionをCATに置き換えることが有効である可能性があります。
4.2. 言語モデリング
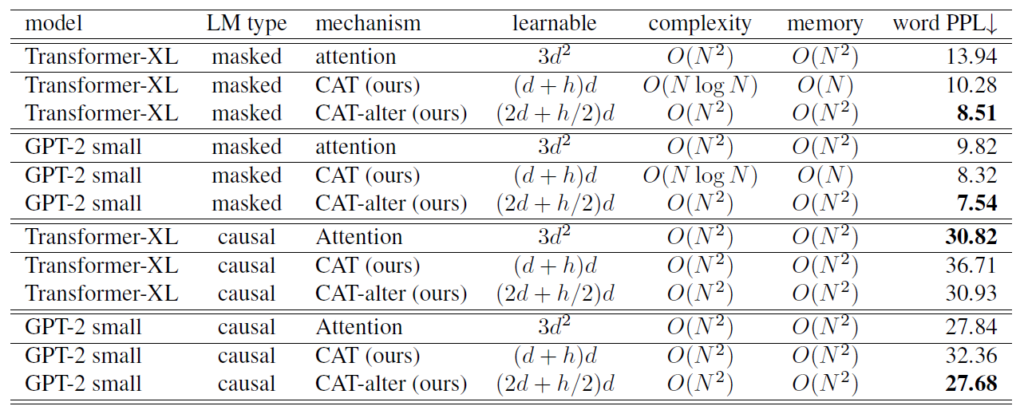
言語モデリングの結果は図3の通りです。LM (Language Modeling) typeとは言語モデルの学習方法を表します。Masked Language Modeling (MLM) は文章中のランダムなトークンが隠され、文章全体から隠されたトークンを予測することで学習します。Causal Language Modeling (CLM) はあるトークン以前の情報のみから、その次のトークンを予測することで学習します。word PPLを比較すると、CATはMLMで従来のAttentionを上回っており、CMLでは下回っています。それに対し、CAT-alterはいずれのLM typeにおいても従来のAttentionに近い、もしくは上回るスコアとなっています。
4.3. 実験結果のまとめ
実験により、CATは精度を欠くことなく計算量を削減する場合があることが確かめられました。特に論文の実験設定では、Average PoolingやMLMの手法が用いられる場合、従来のAttentionをすべてCATに置き換えたモデルで計算量の削減および精度向上が認められました。従来のAttentionの一部をCATに置き換えたCAT-alterのモデルは、論文中のほとんどの設定で従来のAttentionよりも高い精度を示しました。CAT-alterでは従来のAttentionが残っているため最大の計算量は \(\mathcal{O}(N^2)\) のままですが、精度・計算量・メモリなどの観点でCATとAttentionのバランスが取れており、CATに比べて汎用的な手法であるといえます。
おわりに
今回はCATという、精度を落とさずにTransformerの計算量を削減する手法の論文を紹介いたしました。CATはあくまでEngineering-Isomorphic Transformerという枠組みのモデルのひとつであり、柔軟にカスタマイズ可能です。CATのマイナーチェンジ版は論文中でもいくつか紹介されているので、興味のある方はぜひご覧ください。
昨今の多くの生成AIモデルの基礎をなすTransformerに関する研究は盛んに行われています。大規模なモデルの作成に向けて、マシンパワーの増強だけでなく、基礎理論の面からの発展にも引き続き期待が溢れます。
付録
A.1. 巡回畳み込み
配列長 \(N\) の配列 \(a, v\) に対し、巡回畳み込み \(v*a\) は次のように定義されます。
$$ (v * a) [n] := \sum_{m=0}^{N-1}v[m]a[(n-m) \mod N] \tag{A.1} $$
配列を用意して具体的に見てみます。
\(a =[a_0, a_1, \cdots, a_{N-1}], v = [v_0, v_1, \cdots, v_{N-1}]\) とします。これに対し、式 \((\mathrm{A}.1)\) は以下のように書き下されます。
$$ \begin{align*}
(v*a)[0] &= v_0a_0 + v_1a_{N-1} + \cdots + v_{N-1}a_1, \\
(v*a)[1] &= v_0a_1 + v_1a_{0} + \cdots + v_{N-1}a_2, \\
\vdots \\
(v*a)[N-1] &= v_0a_{N-1} + v_1a_{N-2} + \cdots + v_{N-1}a_0.
\end{align*} $$
これは巡回行列を用いて書くことができて、以下が成り立ちます。
$$ v * a = \begin{bmatrix} a_{0} & a_{N-1} & \dots & a_{1} \\ a_{1} & a_{0} & \dots & a_{2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{N-1} & a_{N-2} & \dots & a_{0} \end{bmatrix} \begin{bmatrix} v_0 \\ v_1 \\ \vdots \\ v_{N-1} \end{bmatrix} \tag{A.2} $$
ここで、式 \((\mathrm{A}.2)\) 右辺左側の行列が巡回行列です。
本文中の式 \((3)\) との対応を確認しましょう。式 \((\mathrm{A}.2)\) の巡回行列は \(\mathrm{Roll}(a)\) で表されます。 \(a=\mathrm{softmax}(xW_A)\) とすれば、式 \((3)\) の \(\mathrm{Roll}\) 関数と対応します。式 \((\mathrm{A}.2)\) の \(v\) はベクトルとしましたが、これは \(N \times D\) の2次元行列に容易に拡張可能です。式 \((3)\) の \(xW_V\) は \(N \times D\) の行列 \(v\) に相当します。結局、式 \((3)\) は \(xW_V * \mathrm{softmax}(xW_A)\) の巡回畳み込みを行っていたことがわかります。
A.2. 巡回畳み込みと高速フーリエ変換の関係
巡回畳み込みについては、付録A.1. を参照ください。高速フーリエ変換とは、離散フーリエ変換を高速化したものです。離散フーリエ変換の詳細はここでは省略させていただきますが、定義のみご紹介します。\(N\) 次元の複素ベクトル \(\lbrace x_j \rbrace \ (j \in \lbrace 0, 1, \dots, N-1 \rbrace)\) の離散フーリエ変換 \(\lbrace y_k \rbrace \ (k \in \lbrace 0, 1, \cdots, N-1 \rbrace)\) は以下で定義されます。
$$ y_k := \frac{1}{\sqrt{N}} \sum^{N-1}_{j=0} x_j e^{-2\pi ikj/N} \tag{A.3} $$
以下、高速フーリエ変換とその逆変換をそれぞれ \(\mathrm{FFT}, \mathrm{RFFT}\) で表すことにします。巡回畳み込みの高速フーリエ変換は次のように書くことができることが知られています(離散フーリエ変換でも同様)。
$$ \mathrm{FFT}(v * a) = \mathrm{FFT}(v)\cdot\mathrm{FFT}(a) \tag{A.4} $$
したがって、巡回畳み込みは以下のように計算されます。
$$ v*a = \mathrm{RFFT}\Bigl( \mathrm{FFT}(v)\cdot\mathrm{FFT}(a) \Bigr) \tag{A.5} $$
なお、\(\mathrm{FFT}(v) \cdot \mathrm{FFT}(a)\) は成分ごとに積を取ること(アダマール積)を表し、可換です。
式 \((\mathrm{A}.5)\) 左辺は巡回畳み込みを行っており、この計算量は \(\mathcal{O}(N^2)\) です。一方、右辺は高速フーリエ変換→アダマール積→逆高速フーリエ変換という操作を行っていますが、各操作の計算量はそれぞれ \(\mathcal{O}(N \log N), \mathcal{O}(N), \mathcal{O}(N \log N)\) です。したがって右辺の計算量は \(\mathcal{O}(N \log N)\) となります。このように、高速フーリエ変換によって巡回畳み込みの計算量を削減することができます。
式 \((\mathrm{A}.5)\) に \(v=xW_V, a=\mathrm{softmax}(xW_A)\) を対応付けることにより、式 \((3)\) から式 \((4)\) が導かれます。
参考
[1] Yoshihiro Yamada. CAT: Circular-Convolutional Attention for Sub-Quadratic Transformers. arXiv preprint arXiv:2504.06704v1, 2025.
[2] Russakovsky, O., Deng, J., Su, H. et al. ImageNet Large Scale Visual Recognition Challenge. Int J Comput Vis 115, 211–252, 2015.
[3] M. Cherti et al. Reproducible Scaling Laws for Contrastive Language-Image Learning. 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 2023.
[4] A. Radford et al. Learning Transferable Visual Models From Natural Language Supervision. International Conference on Machine Learning (ICML), 2021.
[5] S. Merity, C. Xiong, J. Bradbury, and R. Socher. Pointer sentinel mixture models. arXiv preprint arXiv:1609.07843, 2016.
[6] Z. Dai et al. Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 2978–2988, Florence, Italy. Association for Computational Linguistics, 2019.
[7] A. Radford et al. Language Models are Unsupervised Multitask Learners. OpenAI, 2019.
