目的

データソリューション事業部の今川です。本記事では、極値統計と空間相関を組み合わせ、降水量データに対して空間的な極値推定を行う方法を紹介します。特に、都道府県ごとの100年に一度の極端な降水量を、空間的な依存関係を考慮してベイズ推定します。

極値統計とは

あるデータの最大値や最小値を用いて、その値がどのような分布になるのかを推論する学問です。

極値統計は、気象、災害リスク、金融など「まれに起こるが影響の大きい現象」を分析するのに有効です。年最大降水量のような「最大値の系列」は、正規分布などでは適切にモデル化できないため、極値理論に基づく特殊な分布（例：Gumbel, Weibullなど）が用いられます。

Gumbel分布

$$ f(x) = \frac{1}{\beta} \exp\left( -\frac{x – \mu}{\beta} – \exp\left( -\frac{x – \mu}{\beta} \right) \right) $$

Gumbel分布は、最大値（または最小値）の極端な値に対する分布です。特に、気象・水文などの「最大降水量」や「最大風速」などの極端現象の記録値をモデル化する際に広く用いられます。右に裾が重く、稀な大きな値が現れる可能性を表現できます。

Weibul 分布

$$ f(x)=\frac{k}{λ} \Big(\frac{x}{λ} \Big)^{k−1}exp\bigg(− \Big(\frac{x}{λ} \Big) ^k \bigg),x≥0 $$

Weibull分布は、寿命や耐久性、強度など「ある閾値を超える確率」を記述するのに適しており、最小値側の極値分布としても使われます。形状パラメータ $k$ によって分布の形が柔軟に変化し、早期故障から長寿命まで多様な現象に対応可能です。

空間相関とは

空間相関とは、「空間的に近い観測点同士の値が類似しやすい」ことを意味します。これは、降水量や気温などの自然現象が連続的に変化するため、地理的に近い地点では似た気象条件が観測される傾向にあるためです。

例えば、岐阜県と長野県は地理的に近いため、似た気象パターンを持つと仮定できます。一方、岐阜県と鹿児島県は距離が遠いため、異なる降水パターンになると考えられます。

モデル概要

本研究では、1995年から2024年までの各都道府県（北海道・沖縄を除く）における年間最大1日降水量のデータを用いて、空間的な極値推定を行います。特に、100年に一度の大雨を推定することを目的としています。そのために、以下の構成要素からなるベイズ階層モデルを構築しています。

1. 観測モデル：Gumbel分布による極値モデル化

各都道府県における年間最大1日降水量は、極値分布であるGumbel分布（第一種極値分布）に従うと仮定します。これは、連続変量の最大値に関する確率分布として古典的に用いられてきたものです。

$$ f(x \mid \mu, \beta_g) = \frac{1}{\beta_g} \exp\left( -\frac{x – \mu}{\beta_g} – \exp\left( -\frac{x – \mu}{\beta_g} \right) \right) $$

2. 潜在変数の空間構造：CAR分布

Gumbel分布のスケールパラメータ $\beta_g$ に対応する潜在変数 $g = (g_1, \dots, g_n)$ は、地理的な近さに基づいて空間的に依存していると仮定します。

この依存構造を表現するために、CAR（Conditional Autoregressive）分布に類似した共分散構造をもつ多変量正規分布を仮定します。

$$ g \sim \mathcal{N} \left( \mu I, \left[ \rho (D – \alpha W) \right]^{-1} \right) $$

$g$：各都道府県に対応する潜在変数ベクトル
$\mu I$：平均ベクトル
$D$：次数行列（各都道府県における隣接数を対角に持つ行列）
$W$：隣接行列（近傍関係を1で示す）
$\alpha \in (0, 1)$：空間相関係数（隣接効果の強さ）
$\rho$：精度（precision）パラメータ

このモデルにより、近接する都道府県同士のパラメータが似た値になるように構造化され、空間的なスムージングが実現されます。

3. パラメータの事前分布

モデル内の未知パラメータには、以下のようなベイズ的な事前分布を設定します：

$$\mu \sim \mathcal{N}(m_\mu, S_\mu)$$

$$\alpha \sim \mathcal{U}(0,1)$$

$$\rho \sim \mathrm{Gamma}(\delta_\rho,\nu_\rho)$$

これにより、モデルの柔軟性を保ちつつ、空間依存性とデータ駆動の推論が可能となります。

実装

過去の降水量を用いて各都道府県の100年に一度の降水量を推測します。

使用データ

1995年から2024年までの各都道府県（北海道と沖縄を除く）の1年あたりの最大の1日の降水量

データの確認

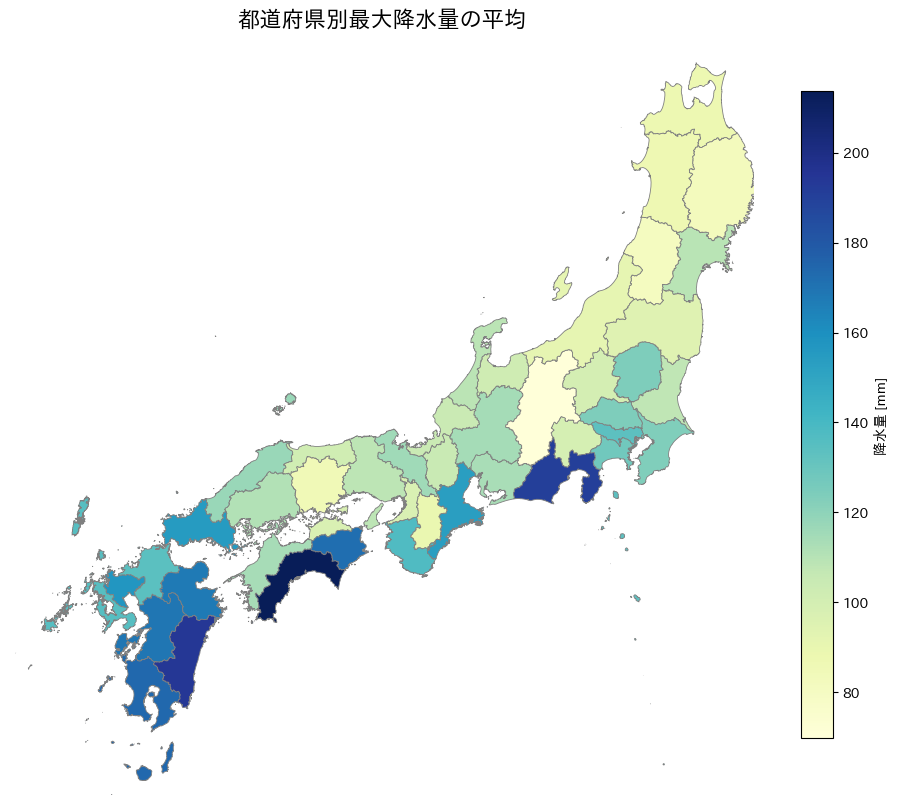
下の図から見て取れるように太平洋沿いの地域の最大の降水量が大きいことが分かります。このことから最大の降水量には空間相関が存在します。

1年あたりの最大の降水量の各都道府県の平均

過去30年あたりの最大の降水量

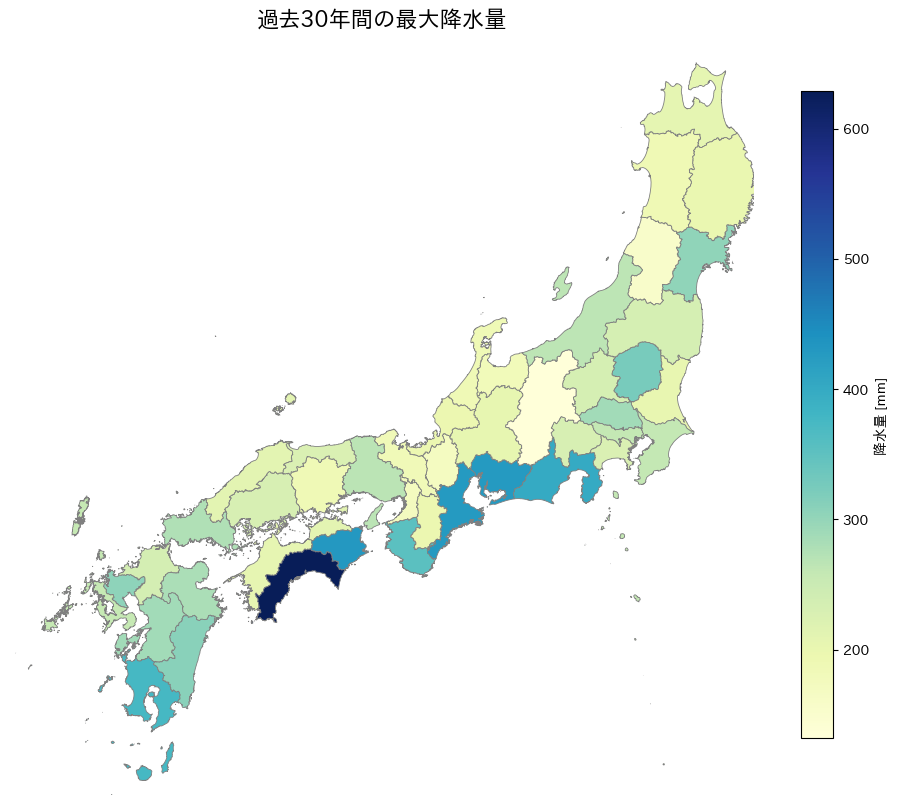
以上の結果より、以下の点が読み取れます。

南海・太平洋側（高知・静岡・宮崎）にピーク

高知県の降水量は600mm超で全国最大
太平洋沿岸の地域は台風・線状降水帯の影響を強く受ける傾向

内陸部・北日本では比較的穏やか

北陸や東北北部では 300mm 未満が多い
雨よりも積雪が多い地域であることが反映されている

隣接行列の確認

隣接行列を作成するためにk近傍(k=3)を用います。これはある都市から最も近い３つの都市を隣接しているとして行列を作成するものです。

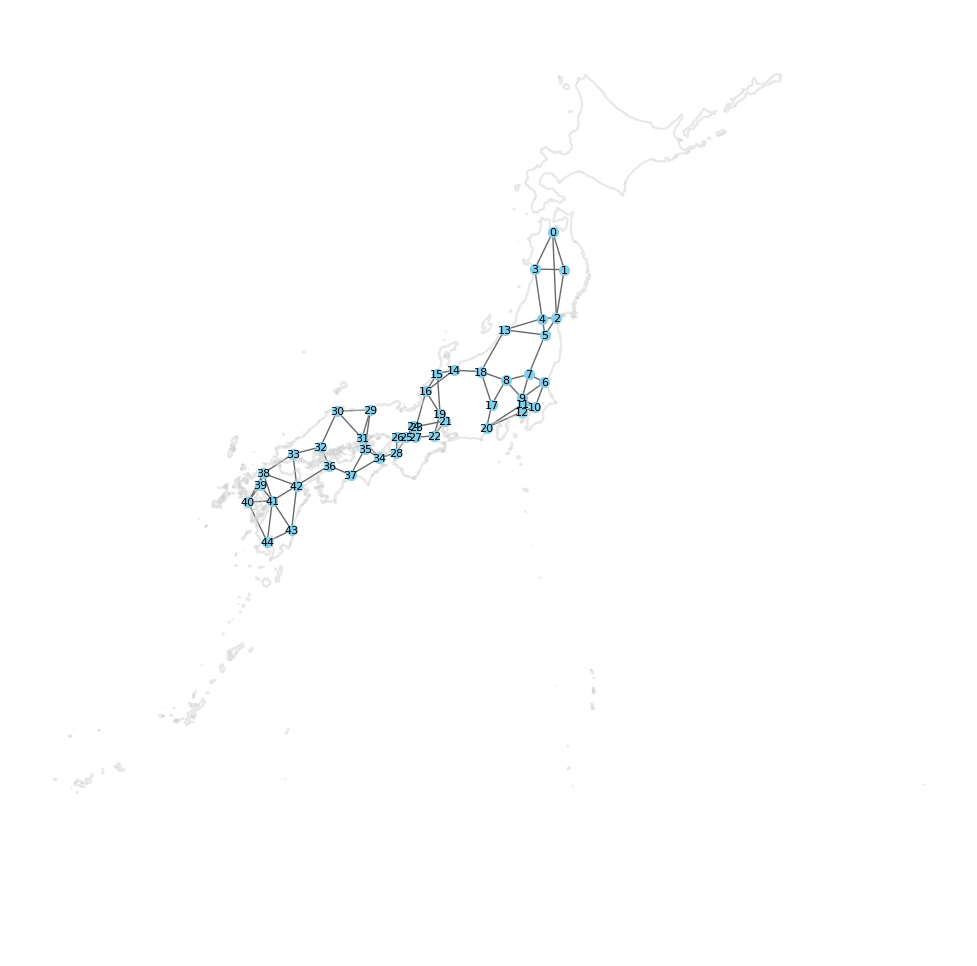
方法

MCMCによる階層ベイズでサンプリングします。その際に事前分布にCAR分布を用いることで空間相関を考慮に入れます。

モデル

def car_precision_matrix(W, alpha, rho):
    # 隣接行列Wの各行の合計を対角行列Dに格納
    D = jnp.diag(jnp.sum(W, axis=1))
    # 精度行列Qを計算
    Q = rho * (D - alpha * W)
    return Q

def gumbel_CAR_model(x, adjacency_matrix, loc_prior_mean=0.0, loc_prior_scale=10.0, delta_rho=2.0, nu_rho=2.0):
    """
    Gumbel-CARモデル
    data: DataFrame (index: rainfall level, columns: city names)
    adjacency_matrix: 都市間の隣接行列（numpy array）
    area_names: 都市名リスト（列順と一致）
    """
    N = x.shape[0]

    # Gumbelの位置パラメータ（固定 or 共通）
    mu = numpyro.sample("mu", dist.Normal(0, 100))

    # CAR事前分布パラメータ
    mu_g = numpyro.sample("mu_g", dist.Normal(loc_prior_mean, loc_prior_scale))
    alpha = numpyro.sample("alpha", dist.Uniform(0, 1))
    rho = numpyro.sample("rho", dist.Gamma(delta_rho, nu_rho))

    # 精度行列とその逆行列のCholesky分解
    Q = car_precision_matrix(adjacency_matrix, alpha, rho)
    Q_stable = Q + 1e-5 * jnp.eye(N)  # 数値安定化
    L = jnp.linalg.cholesky(jnp.linalg.inv(Q_stable))

    # 空間効果の潜在変数
    g = numpyro.sample("g", dist.MultivariateNormal(loc=mu_g * jnp.ones(N), scale_tril=L))
    beta = jnp.exp(g)

    # Gumbel分布による観測
    numpyro.sample("obs", Gumbel(loc=mu, scale=beta), obs=x)

モデル構造

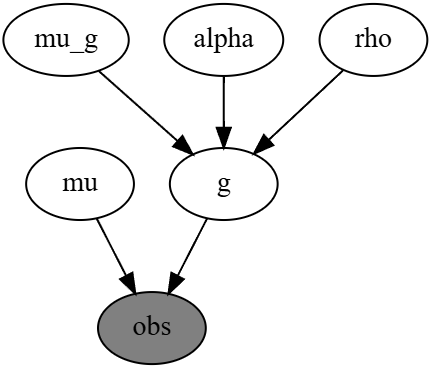
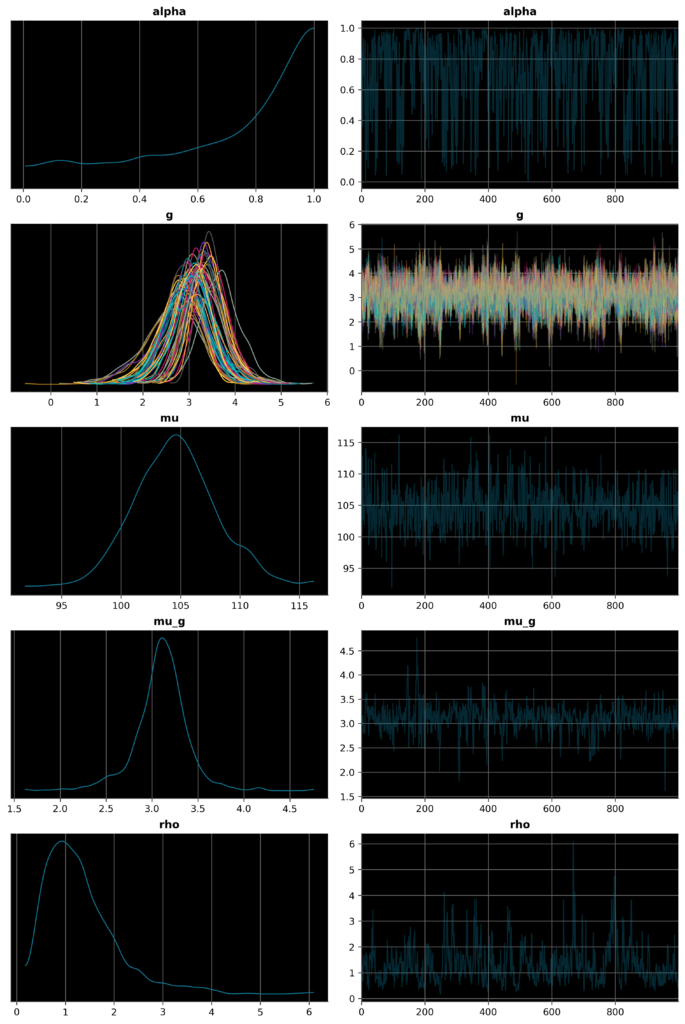
収束結果

予測

100年に１度の量の降水量を推定します。

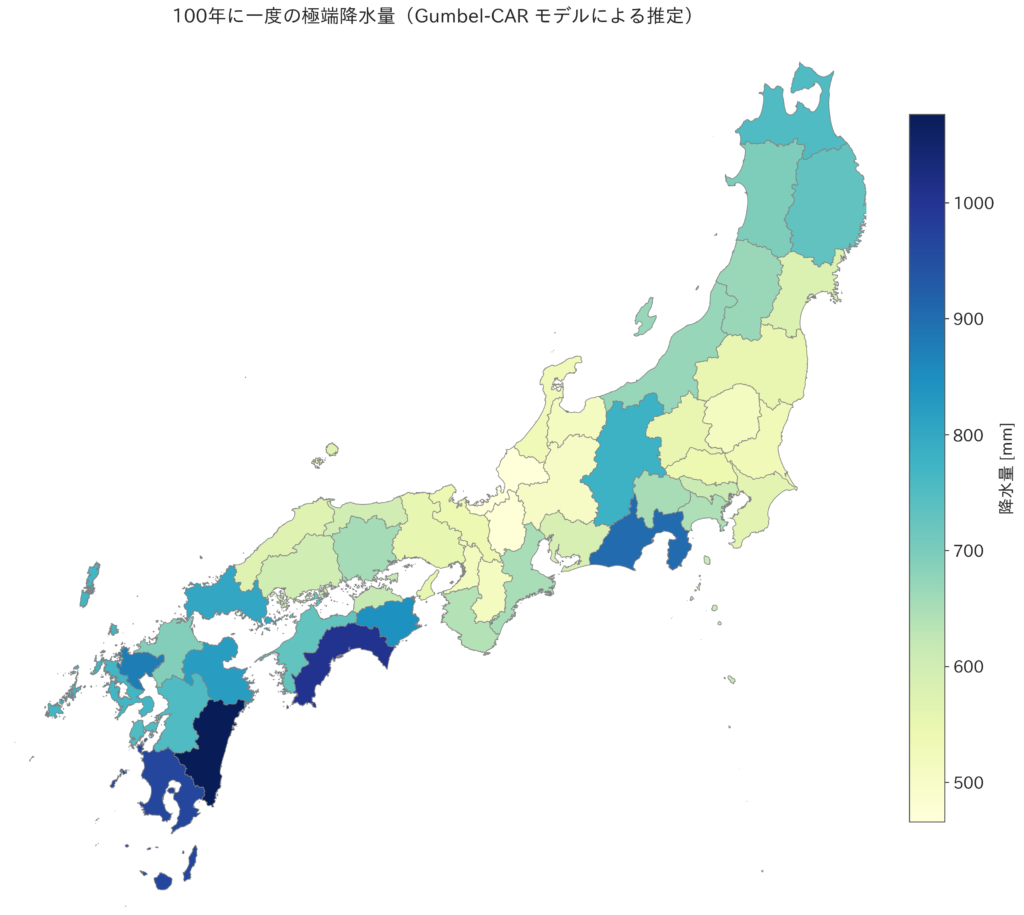
考察

1. 南西日本（特に九州南部と四国）で極端降水量が顕著

宮崎県・鹿児島県・高知県を中心に、1000mm超の予測値
台風の進路や南海トラフからの湿った空気の流入の影響を強く受ける地域で、実際の豪雨災害も多い。
Gumbel-CARモデルは空間的連続性を保ちながら高値を示しており、物理的妥当性が高い。

2. 関東内陸部や中部山岳地帯にも局所的なピーク

静岡・岐阜・長野など：**地形性降水（地形の影響で強化された降水）**を反映。
CAR構造により、これらの高値が近隣地域にもなだらかに伝播していることがわかる。

3. 東北・北海道・北陸の比較的低い降水リスク

東北北部や日本海側では、年最大降水量が600〜700mm程度。
気候的には冬の降雪が主で、夏季の豪雨は相対的に少ない。
モデルはこの傾向を反映しつつ、空間スムージングにより滑らかな分布になっている。

4. 一部地域（長野県など）でズレが出た理由

過去30年の1年あたりの最大の降水量のデータに分散が大きい。
近くに高降水地域に囲まれており空間的に引っ張られやすい。

まとめ

本記事では、空間相関を考慮した極値統計モデルを用いて、100年に一度の降水量をベイズ推定により評価しました。このような手法は、気象リスクの評価やインフラ設計、さらには気候変動影響の地域評価にも応用可能です。今後は、気候モデル出力との統合や時系列的な変化の導入も検討されるべき課題です。

引用

気象庁：https://www.data.jma.go.jp/stats/etrn/index.php

オウンドメディアも運営しています

この記事がよかったら
シェアしてください。

100年に一度の大雨をどう予測するか？ 空間極値統計による降水量推定

目的