お気軽にお問い合わせください
多値分類が可能な多項ロジスティック回帰分析について詳しく解説!

多項ロジスティック回帰分析とは
多項ロジスティック回帰分析(Multiple Logistic Regression)とは、3つ以上のカテゴリの中でどのカテゴリに分類されるかを予測する統計的手法です。
この手法を用いることで、消費者の特性(性別や職業、行動の記録)などから、どの自社サービスが選択されるかを予測することができます。
この分析手法における利点の1つは、各選択肢が選ばれるか、選ばれないかの2択ではなく、全ての選択肢に対して選択される確率を求めることができる点にあります。そのため多様な結果の解釈を可能にします。
二項ロジスティック回帰分析と多項ロジスティック回帰分析との違い
二項ロジスティック回帰分析は、ある事象の発生有無などの二値分類の分析手法です。目的変数が「0 or 1」など二値であればこの手法を使うことで、ある事象が発生するか否か、その確率を予測することが可能です。

一方、多項ロジスティック回帰分析は、多値分類の分析手法です。目的変数が「A, B, C, …」のように3つ以上のカテゴリ値をとる場合に使用することで、目的変数がそれぞれの値をとる確率を予測することが可能です。
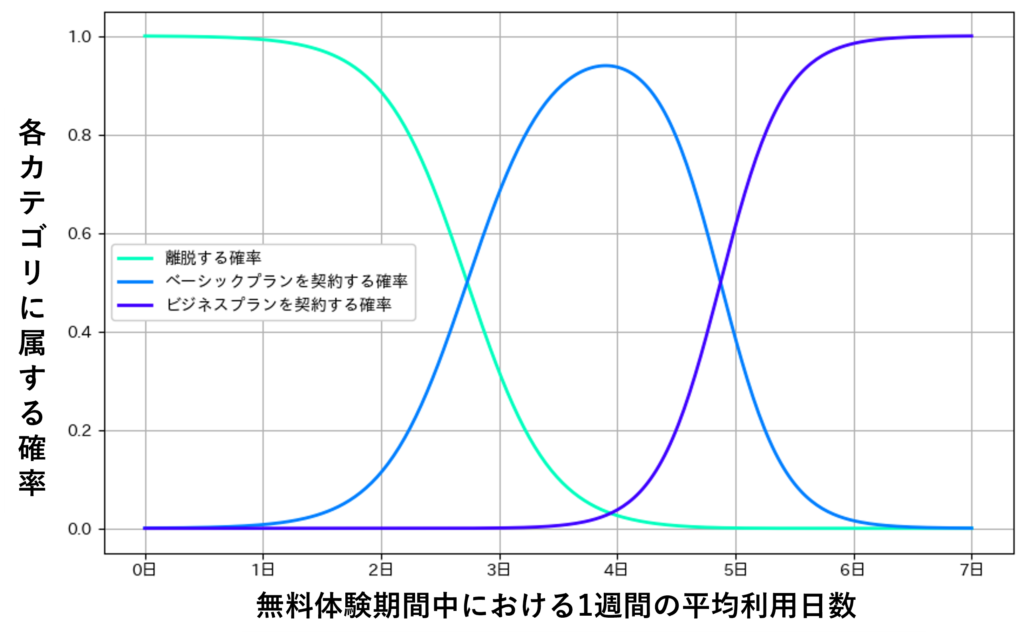
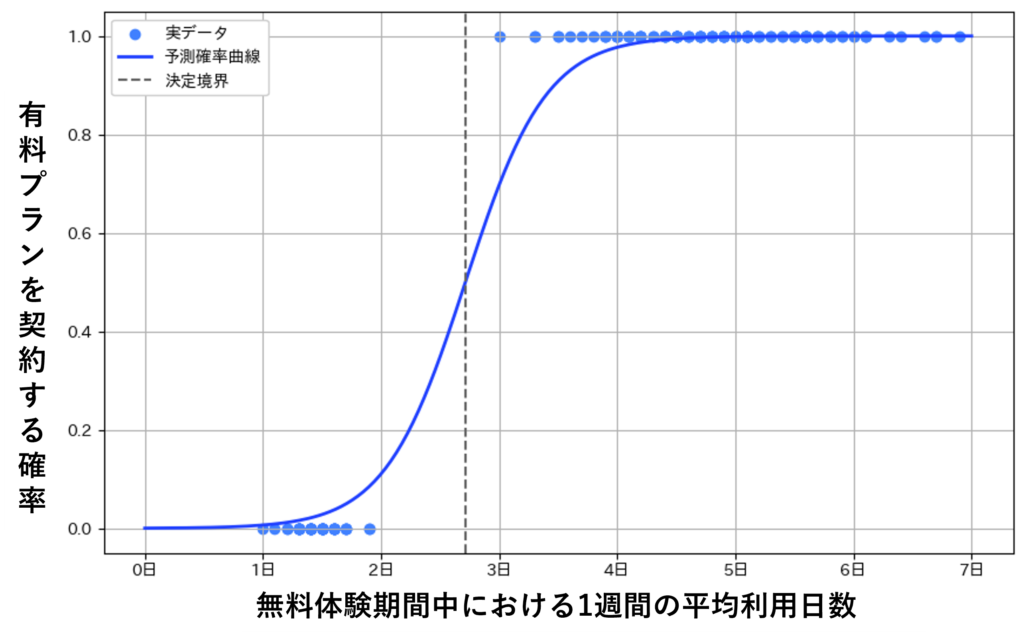
具体例として、顧客が自社サービスを30日間無料体験した後に、ベーシックプラン、ビジネスプランのどちらを契約するのか、あるいは離脱するのかを予測したい場合を考えます。
二項ロジスティック回帰分析では、ある顧客が有料プランを契約するか否かを予測することが可能であるのに対し、多項ロジスティック回帰分析ではベーシックプランを契約する確率、ビジネスプランを契約する確率、どちらも契約せず離脱する確率を求め、どの確率が最も高いかを予測することが可能です。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。多項ロジスティック回帰分析をはじめ、機械学習による分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
必要なデータ
続いて、多項ロジスティック回帰分析の際に必要なデータについて解説します。
分析には2種類のデータが必要です。
まず1つ目は、目的変数として使用するデータです。
目的変数は分類予測したい変数であり、3種類以上の値をとる質的データである必要があります。
売上などの量的データに対しても、月間利用額3万円以上をロイヤル客層、1~3万円を得意客層、1万円以下を一般客層と区分し、ビン化することで目的変数として使用することができます。
もう1つは、説明変数として使用するデータです。
説明変数は分類予測をするために必要な変数で、その情報がわかっていることで予測が当たりやすいと考えられる変数です。
性別や職業などの2種類以上の値をとる質的データに加えて、年齢などの量的データも使用することができます。
「二項ロジスティック回帰分析と多項ロジスティック回帰分析との違い」で紹介した具体例と同じく、顧客が自社サービスを30日間無料体験した後に、ベーシックプラン、ビジネスプランのどちらを契約するのか、あるいは離脱するのかを予測したい場合では、性別(質的データ)、年齢(量的データ)、職業(質的データ)、サイトのアクセス頻度(量的データ)、無料体験期間中における1週間の平均利用日数(量的データ)、自社サービスへの満足度(質的データ)などを説明変数として使用することができます。
分析に使用するデータは全て数値である必要があるため、性別のデータも男性 = 1、女性 = 0と数値に変換するダミー変数化をすることで分析に使用することができます。(男性 = 0、女性 = 1とすることも可能です。)
また、目的変数として使用するデータについても、ベーシックプラン、ビジネスプラン、離脱を1, 2, 3に変換しておく必要があります。
しかし、上記のようにして用意したデータを全て使用し、分析・予測をおこなえば良いというわけではありません。より正確かつ効果的な分析・予測をおこなうためには注意しなくてはならない点があります。こちらについては本記事の後半で解説いたします。
多項ロジスティック回帰分析のビジネス活用例
次に、ビジネスシーンでの活用例を紹介いたします。
アンケートデータを用いたブランドイメージ分析
企業の「技術力がある」というイメージを向上させる要因を特定するために、消費者に対してアンケートを実施し、多項ロジスティック回帰分析を用いて分析した例を紹介します。
アンケートの質問項目には、目的変数として使用する質問である「技術力がある」に加えて、企業がおこなっている様々な活動に対する印象を調査します。
| 回答者ID | 技術力がある | CSR活動を 積極的におこなっている | 事業投資を 積極的におこなっている | … |
|---|---|---|---|---|
| 100001 | そう思う | ややそう思う | そう思う | … |
| 100002 | どちらともいえない | ややそう思う | ややそう思う | … |
| 100003 | あまりそう思わない | 回答なし | あまりそう思わない | … |
| 100004 | ややそう思う | あまりそう思わない | どちらともいえない | … |
| 100005 | ややそう思う | そう思わない | どちらともいえない | … |
| … | … | … | … | … |
アンケートで得られた回答をそのまま説明変数として使用することはできないので、回答を数値に変換します。具体的には「そう思う」を1、「そう思わない」を5に変換します。
また、欠損がある回答データは分析に使用できないため、削除するなどの対応が必要です。
| 回答者ID | 技術力がある | CSR活動を 積極的におこなっている | 事業投資を 積極的におこなっている | … |
|---|---|---|---|---|
| 100001 | 1 | 2 | 1 | … |
| 100002 | 3 | 2 | 2 | … |
| 100004 | 2 | 4 | 3 | … |
| 100005 | 2 | 5 | 3 | … |
| … | … | … | … | … |
整形したデータを用いて多項ロジスティック回帰分析をおこなった結果、以下のようなグラフになります。
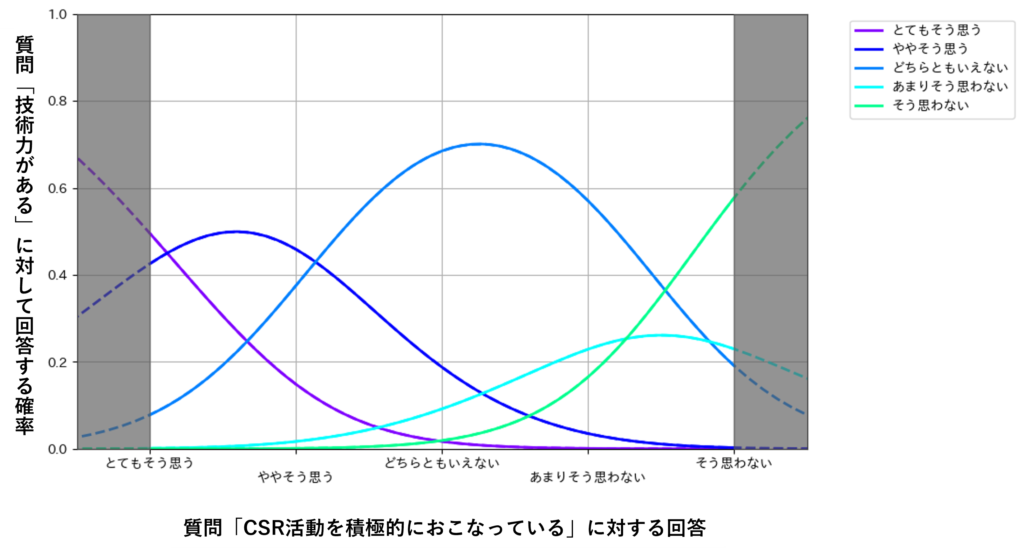
ビジネスの意思決定には、よりわかりやすい分析結果・グラフの提示を求められる場合があります。
上記のグラフでは、目的変数の選択肢「とてもそう思う」と「ややそう思う」の波形、「そう思わない」と「あまりそう思わない」の波形がそれぞれ似た形をしているため解釈がしずらく、意思決定に活用しにくいです。
そのため、目的変数の選択肢に対して回答を集約するなどして、ビジネスの意思決定に活用することができます。
今回の例では、目的変数である質問「技術力がある」の回答に対して、「とてもそう思う」と「ややそう思う」を「そう思う」として集約し、「そう思わない」と「あまりそう思わない」を「そう思わない」として集約しました。
このようにしてデータを加工し、分析した結果、以下のようなグラフになります。
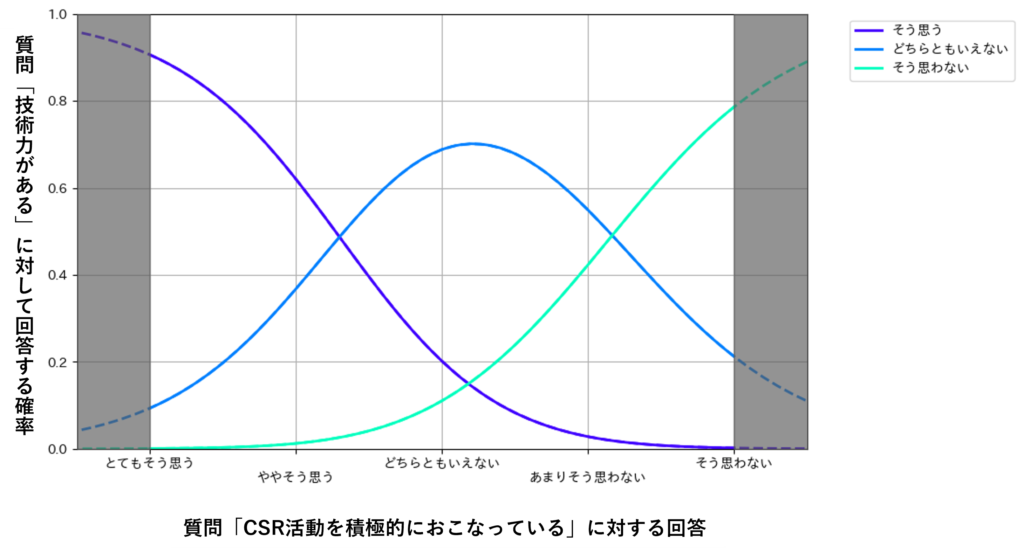
このグラフから、質問「CSR活動を積極的におこなっている」に対して「とてもそう思う」、「ややそう思う」と回答した人は、質問「技術力がある」に対しても「そう思う」と回答する確率がぞれぞれ約90%、約60%と非常に高く、他の目的変数の選択肢と比較して選ばれやすいということがわかります。
その他の活用例
その他、ビジネスシーンでの活用事例として以下2つを紹介いたします。
マーケティング施策のターゲット特定
マーケティングの分野における活用例として、特定のターゲットに効果的な施策を展開するための要因分析があります。
具体的には、新商品のフレーバーやイメージカラーなどに対して、消費者の反応を分析するため使用されました。説明変数として、過去の販売データや消費者の属性情報などを使用し、どのような情報が購買意欲に影響を与えるかを分析しました。
その結果をもとに、ターゲットセグメントを特定し、その層に対してマーケティング施策を展開することで、売上を大きく伸長させることができました。また、多項ロジスティック回帰分析の結果を活用することで新商品の開発にも成功しており、消費者ニーズにこたえる製品を市場に投入することが実現しています。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。多項ロジスティック回帰分析をはじめ、機械学習による分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
その他分野における活用例
マーケティング分野以外にも医療分野で活用された事例があります。
医療分野では、特定の病気の発症リスクを予測するために、この分析手法が使用されました。患者の病歴や生活習慣などのデータを用いて分析することで、生活習慣や遺伝的要因が病気の発症に与える影響を評価しました。多項ロジスティック回帰分析の結果やその他の分析結果を踏まえ、特定の生活習慣が病気のリスクを高めることが明らかになり、予防措置が可能になりました。
注意点
最後に多項ロジスティック回帰分析の注意点について紹介いたします。
過学習への対処
過学習とは、多項ロジスティック回帰分析を含めた機械学習において、学習に使用したデータに対する当てはまりは良いが、未知のデータに対しては、当てはまりが悪くなってしまう状態をさします。分析に用いるデータの数が極端に少ない場合や、予測に使用する説明変数が極端に多い場合に、過学習が発生する可能性があります。
過学習が発生している状態で分析結果をビジネスや意思決定へ活用すると、誤った判断をしてしまう可能性が高くなります。そのためデータ整形やモデリング、説明変数の選択などで適切に対処し、テストデータ(モデルの学習時には使用していないデータ)を用いてモデルを評価することが必要です。
不均衡データへの対処
目的変数の分布が極端に偏っている場合、適切に対処する必要があります。
目的変数がA, B, Cの3つのカテゴリで、カテゴリAのデータが全体の7割、カテゴリBのデータが全体の2割、カテゴリCのデータが全体の1割である場合、目的変数の分布が偏っており、不均衡データになっています。
このような状態で分析してしまうと、過学習の場合と同じく、未知のデータに対する当てはまりが悪くなってしまいます。
不均衡データへの対処法として、アンダーサンプリングやオーバーサンプリングが存在します。これらの手法を用いて、学習の際に目的変数の数が各カテゴリで一致するように調整し、適切なモデルを作成する必要があります。
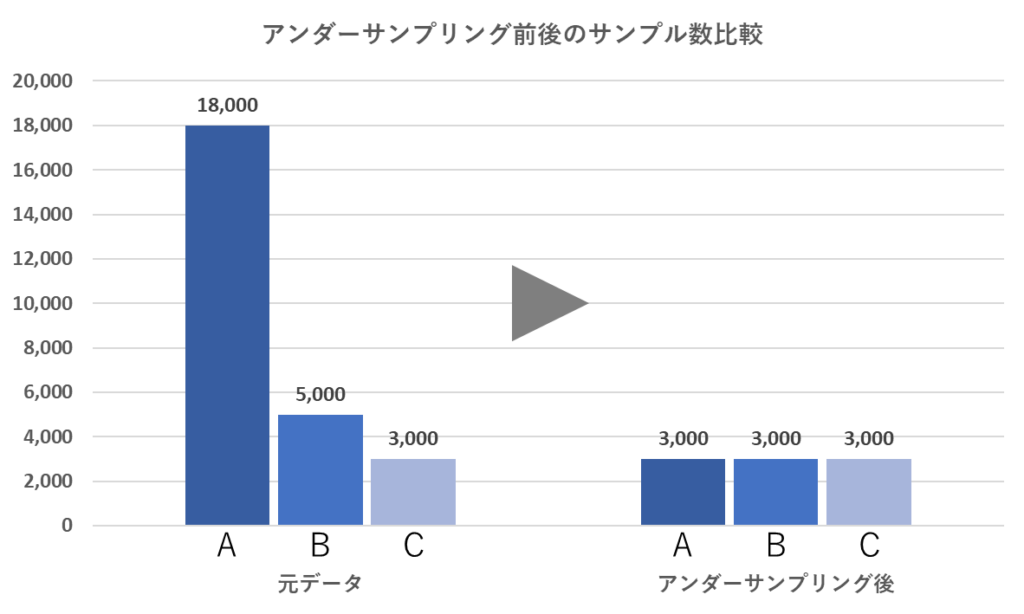
アンダーサンプリング
少数派のデータ数に合わせて、多数派のデータの一部だけを学習に使用する手法。
データの選択には、ランダムにデータを選択する方法や、少数派のデータに近いデータを選択するニアミス法などがあります。
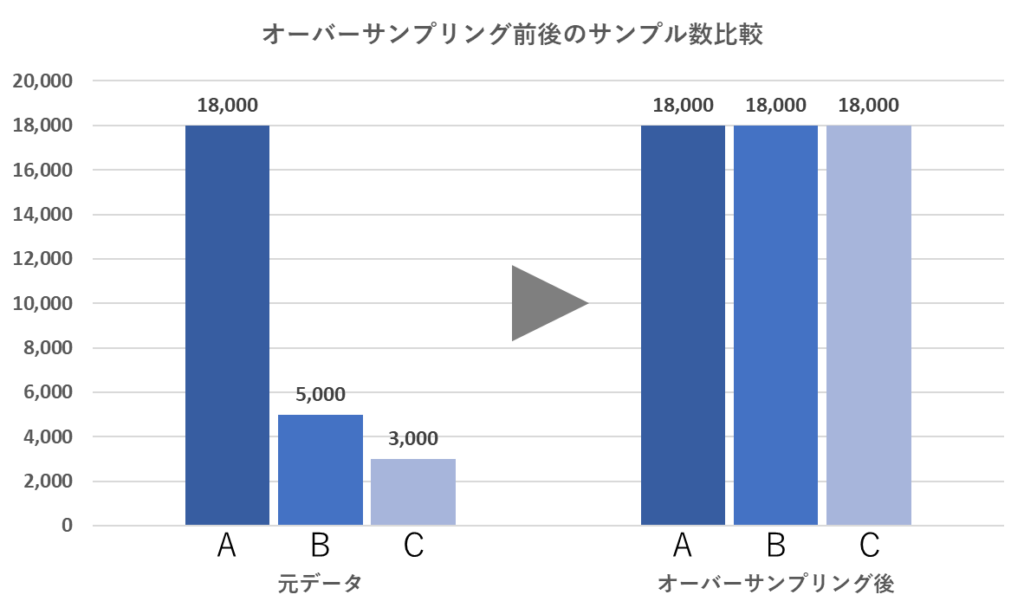
オーバーサンプリング
多数派のデータ数に合わせて、少数派のデータを水増しする手法。
データを増やす手法として、近接するデータ間に新しいサンプルを内挿するSMOTEなどがあります。
切片をモデルに含めるか否かを検討する
回帰モデルを作成する際に切片をモデルに含めるか否かを検討する必要があります。
切片を含む回帰モデルでは全ての説明変数が0の値をとる時、予測値は切片によって決まります。
これに対して、切片を含まない回帰モデルでは全ての説明変数が0の値をとる時、切片の影響を受けないため、多項ロジスティック回帰モデルの場合、目的変数の各カテゴリに属する確率が全て等しいという予測になります。(二項ロジスティック回帰モデルでは事象の発生確率が50%という予測になり、重回帰モデルの場合は目的変数が0という予測になります。)
ロジスティック回帰モデルでは、全ての説明変数が0の値をとる時、各カテゴリに属する確率が全て等しくなる(重回帰モデルでは予測値が0になる)ことが理論上正しか否かを慎重に検討し、切片を含めるか、含めないかを決める必要があります。
ベースカテゴリの選択に注意する
多項ロジスティック回帰分析では、ベースとなるカテゴリを設定する必要があります。
分析結果の解釈は、ベースカテゴリと比較して特定のサブカテゴリに属する確率がどれだけ高いか、低いかということになります。
そのため、選択したベースカテゴリによって、計算の結果得られる回帰係数や符号が異なります。
ビジネス活用例で紹介した具体的を用いると、質問「技術力がある」に対する回答の確率を予測するモデルで、ベースカテゴリを「そう思わない」と回答する確率、「どちらでもない」と回答する確率、「そう思う」と回答する確率と設定する場合では、以下の表のように分析の結果得られる係数の大小や符号が変わります。
どれをベースカテゴリとしてもモデルの精度自体は変わりませんが、分析結果が解釈しやすくなるように試行錯誤したり、分析設計する必要があります。
| ベースカテゴリ | サブカテゴリ | 質問「CSR活動を積極的におこなっている」 の係数 | p値 | … |
|---|---|---|---|---|
| そう思う | どちらでもない | 0.045 | 0.727 | … |
| そう思わない | -0.235 | 0.249 | … | |
| どちらでもない | そう思う | -0.045 | 0.727 | … |
| そう思わない | -0.280 | 0.092 | … | |
| そう思わない | そう思う | 0.235 | 0.249 | … |
| どちらでもない | 0.280 | 0.092 | … |
多重共線性の確認
多項ロジスティック回帰モデルに加え、重回帰モデルなどの回帰モデルでは、説明変数同士の中で相関が高い変数が存在すると不安定なモデルになってしまい、正しい評価ができなくなってしまう事象が発生します。これが多重共線性の問題です。
ビジネス活用例で紹介した具体的では、説明変数に企業のイメージを問う質問項目を使用していますが、「顧客の要望に柔軟に対応している」と「利用者の声を大切にしている」という質問項目を説明変数として入れた場合、多重共線性が発生する可能性があります。これは2つの質問内容が似ており、相関が高いと考えられるためです。
質的データ同士がどれほど相関があるかを数値で確認する際には、「クラメール連関係数」を用いて評価することができます。
また、「二項ロジスティック回帰分析と多項ロジスティック回帰分析との違い」で紹介した具体例、顧客が自社サービスを30日間無料体験した後に、ベーシックプラン、ビジネスプランのどちらを契約するのか、あるいは離脱するのかを予測したい場合では、「サイトのアクセス頻度」と「サイト内滞在時間の合計」を説明変数に加えた場合、多重共線性が発生する可能性があります。これは「サイトのアクセス頻度」が高いほど「サイト内滞在時間の合計」も増加するため、相関が高いと考えられるためです。
上記のように量的データ同士、質的データ同士の相関だけではなく、質的データと量的データの相関も確認する必要があります。質的データと量的データの相関は「相関比」という指標で評価することできます。
多重共線性を回避する別の方法として、主成分分析を用いた変数合成があげられます。
主成分分析は、相関が高い変数同士を合成し変数の数を減らす手法で、その合成変数を回帰モデルに使用することができます。これにより、多重共線性を回避した形でモデリングすることが可能になります。
一方で、合成した変数の意味付づが難しく、結果の解釈が困難になるデメリットもあります。
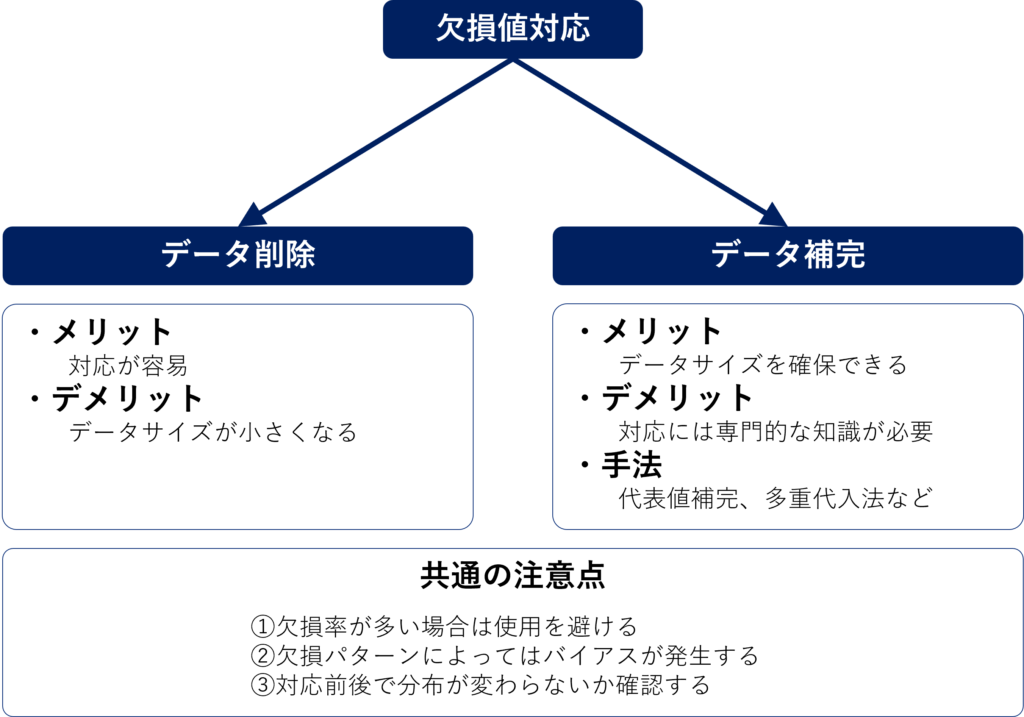
データの欠損を確認する
分析に使用する変数のデータが欠損している場合、そのままでは分析に使用できないため、状況に応じて適切に対処する必要があります。
大きく分けて2つの処理方法があり、欠損しているデータを削除する方法と、データを代入し欠損箇所を補完する方法です。
データを削除する場合は、削除後のデータサイズが小さくなりすぎないか、削除する前後でデータの分布が大きく変わっていないことを確認する必要があります。
データを補完する場合は、「0」などの定数や、該当データの平均値・中央値などの代表値、他のデータを使用し多重代入法などで予測した推定値などを用いて補完することが可能です。データを削除する場合と同様にデータを補完する前後でデータの分布に変化が無いことを確認する必要があります。
特に活用例で紹介したオンラインアンケートの場合、回答次第では別の回答が一部欠損した状態で納品される可能性があります。回答データを削除または補完する場合は、扱い方を慎重に決める必要があります。
データの欠損確認は、分析の前処理として必ず実施すべき事項です。
選択した欠損値対応によって、その後の分析や予測モデルの精度にも影響があるため、欠損処理データの特性を理解したうえで、ステークホルダーの納得感・合理性のもとに分析を進めていく必要があります。
まとめ
多項ロジスティック回帰分析では多値分類が可能なため、二項ロジスティック回帰分析と比較して多様な結果の解釈が可能になります。
マーケティング分野や医療分野など様々な分野で、多項ロジスティック回帰モデルが適用可能なため汎用的な分析手法として知られています。
一方、より正確に分析するために多重共線性や過学習、ベースカテゴリの選択など注意するべき点があるため慎重に分析する必要があります。
本記事が多項ロジスティック回帰分析の特性や注意点を踏まえた、一歩深い分析の役に立てれば幸いです。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。多項ロジスティック回帰分析をはじめ、機械学習による分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
データアナリティクスラボ株式会社での仕事に興味のある方はぜひ採用サイトをご覧ください!














