生存時間分析とは？イベント発生までの時間を分析する手法を解説！

生存時間解析とは

生存時間解析における「生存時間」とは、「あるイベントが発生するまでの時間」のことであり、その時間を分析する手法を総称して「生存時間解析」と呼びます。

生存時間解析の目的は、イベント発生までの時間の分布を明らかにすること、特定の要因が生存時間に与える影響を評価することにあります。データの観測期間内でイベントが発生しなかったケースである「打ち切り」を考慮できる点が特徴です。

以下の図は、3人の観察対象者について、観察期間におけるイベントの発生および打ち切りの状況を示しています。Cさんは観察期間の終了時点でイベントが発生しておらず、打ち切りとして扱われます。生存時間解析では、このようにイベントが発生しなかったケースも無視せず、「観察期間中の5年間でイベントが起こらなかった」という情報を取り入れて解析に活用します。

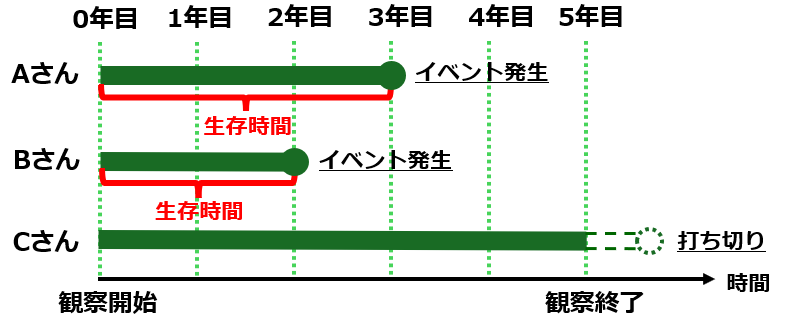
「生存時間解析」という名称は、もともと医療分野で患者の生存期間を分析する目的で発展したことに由来しますが、現在では「生存時間＝イベントが発生するまでの時間」「死亡=イベント発生」として捉えられ、製造業や金融など多様な分野で活用されています。

生存時間解析によってわかること

生存時間解析によってわかることは大きく分けて以下の3つです。

以下それぞれ簡単に解説します。

・生存割合推移の分布

経時的なイベント発生割合の推移がわかります。
例えば、がん患者を5年間追跡し、1年後、3年後、5年後の生存割合がどのように変化するかを推定することができます。

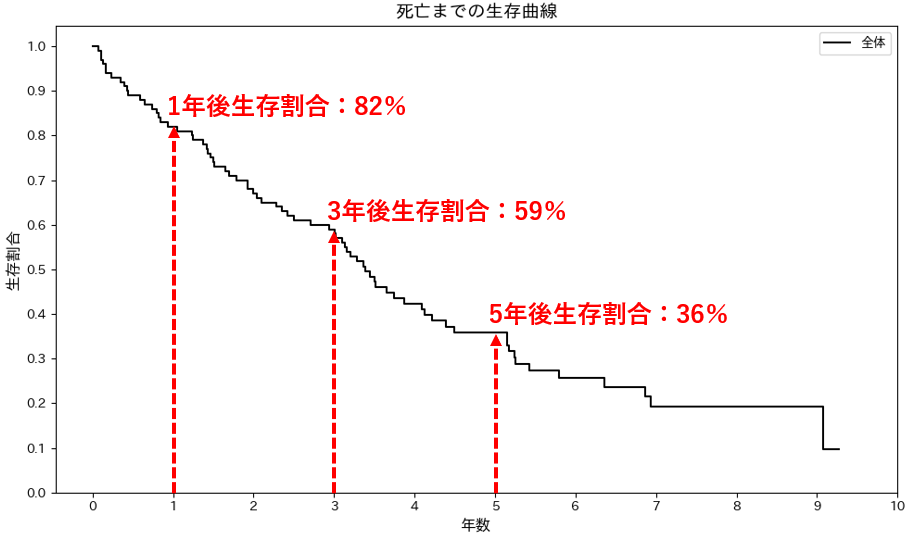
・グループ間の生存割合推移の違い

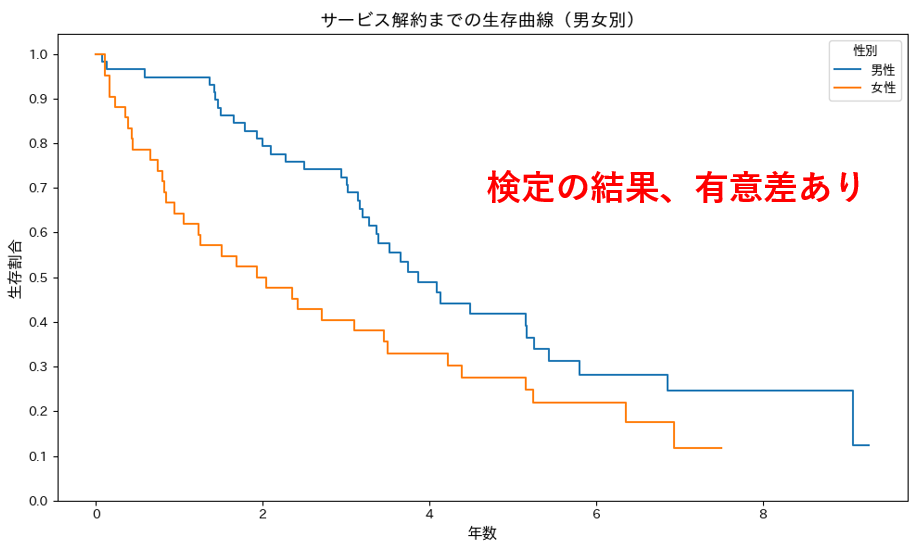
異なる因子のグループ間で生存割合推移を比較し、差があるかを定量的に確認できます。
例えば、あるサービスについて、男性と女性で解約割合推移に差があるかどうかを検定により判断できます。

・イベント発生リスクに影響を与える因子

イベント発生リスクに影響を与えそうな因子を統計モデルを用いて分析し、その影響の大きさを評価できます。
例えば、薬剤Aを使用すると死亡リスクがどの程度低下するかを数値で算出することができます。具体的には、「薬剤Aを使用することで死亡のリスクを10%低下させることができる」のような表現ができます。

生存時間解析の代表的な手法

ここでは、生存時間解析における代表的な3つの手法について紹介します。

カプランマイヤー法

カプランマイヤー法は、生存関数S(t)を推定する手法です。生存関数S(t)とは、「時点tまでにイベントが発生せずに生存している確率」を表す関数です。

生存関数S(t)は、各イベント発生時点ごとに次の式で更新されます。

$$
S(t) = \prod_{i: t_i \leq t} \frac{n_i – d_i}{n_i}
$$

この数式は、「ある時点で生存している確率は、それ以前の全ての時点で生存していた確率の積」として表されます。カプランマイヤー推定の結果は、生存曲線として可視化されます。生存曲線は、生存関数 S(t) の推定値をグラフ化したもので、時間の経過に伴う生存割合の変化を示します。

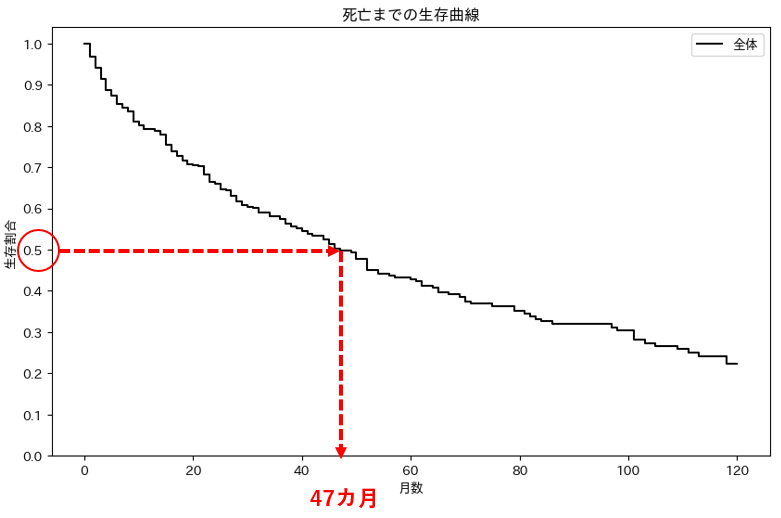
実際のがん患者データを用いてカプランマイヤー推定を行い、生存曲線をプロットすると下図をプロットすることができます。プロットされた生存曲線は、がんを発症した後の生存割合の推移を示しています。

縦軸は生存割合、横軸は経過時間（月）を表しており、時間の経過とともに生存割合がどのように変化するのかを把握することができます。グラフから、がん発症後の生存割合が50%となるのは47か月後であることが読み取れ、半数の患者がこの時点までは生存していることがわかります。

ログランク検定

ログランク検定は、2つ以上のグループの生存曲線に統計的な差があるかどうかを検定する方法です。帰無仮説を「グループ間で生存曲線に差はない」としたときのp値が算出されます。

ログランク検定は、各時点tiでイベントが発生した人数をもとに、以下のように期待されるイベント数と実際のイベント数の差を評価します。
検定統計量\(\chi^2\)は、次の式で計算されます。

$$
\chi^2 = \sum_i \sum_j \frac{(O_{ji} – E_{ji})^2}{V_i}
$$

この統計量がカイ二乗分布に従うことからp値を算出します。得られたp値と事前に設定していた有意水準から帰無仮説を棄却するか判断します。

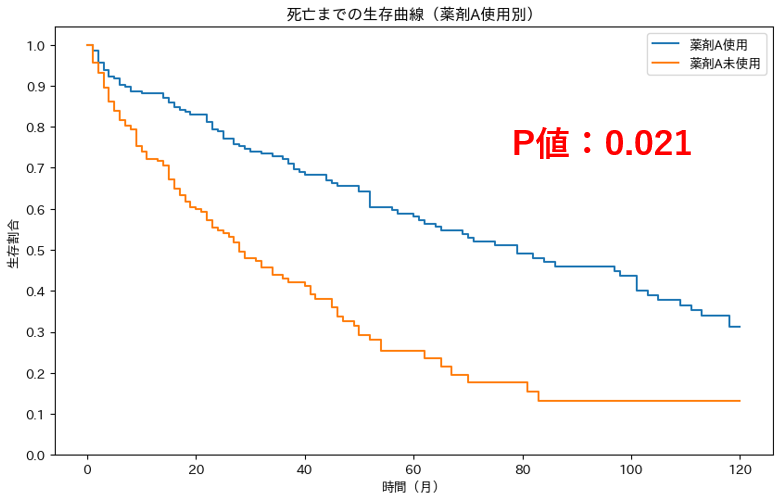
例えば、ある薬剤Aを使用した患者と使用していない患者の経時的な生存割合に差があるかをログランク検定で確認します。
以下の図の結果にてp値が0.021より、薬剤Aを使用した群と使用しない群は有意差があると言えます（有意水準5％の場合）。

Cox回帰（Cox比例ハザードモデル）

Cox回帰は、ハザード関数を推定することで、説明変数がイベント発生リスクにどの程度関係しているかを定量的に明らかにする手法です。
ログランク検定では、「ある因子」で分けたグループ間で、生存割合に統計的な差があるかどうかを判断していました。一方でCox回帰は、「ある因子」がイベント発生リスクに対してどれだけ影響を与えるかを、ハザード比（HR）として算出する手法です。

Cox回帰モデルの基本式は以下のように表されます。

$$
h(t \mid \mathbf{X}) = h_0(t) \cdot \exp(\beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p)
$$

例えば、薬剤Aが死亡リスクにどれくらい影響しているかをCox回帰モデルを用いて評価できます。Cox回帰を実行すると以下のような結果が出力されます。薬剤Aに関してp値が0.05未満、ハザード比が0.83であるため、薬剤Aを使用すると死亡リスクが17%低下することがわかります。

説明変数	回帰係数（β）	ハザード比（exp(β)）	p値
年齢	0.11	1.12	0.03
性別（男性:0, 女性:1）	-0.08	0.92	0.02
身長	0.01	1.01	0.09
体重	0.09	1.09	0.08
薬剤A（未使用:0, 使用:1）	-0.19	0.83	0.01

Cox回帰は比例ハザード性が成り立っている必要があります。
比例ハザード性とは、「ハザード比は時間経過に依存せず一定である」という仮定です。つまり、ある説明変数がイベント発生リスクに与える影響は時間が経過しても変わらないと仮定しています。

比例ハザード性を確認する方法の1つとして、生存曲線の交差をチェックすることが挙げられます。具体的には、生存曲線をグループ別に描画し、その形状を比較します。もし生存曲線が時間の経過とともに大きく交差している場合、ハザード比が一定ではなく時間依存的に変化している可能性があり、比例ハザード性の仮定が成り立っていない可能性があります。

必要なデータ

生存時間解析は、あるイベントが発生するまでの時間（生存時間）に着目します。そのため、対象ごとに「追跡開始時点」と「イベント発生日または追跡終了時点」を記録したログデータが必要です。これをもとにイベント発生までの時間を算出し、分析に用います。さらに、対象の情報（説明変数）を加えることでそれぞれの説明変数がイベント発生リスクにどの程度影響を与えているのかを定量的に評価できます。

この際に重要なのが「打ち切り」の扱いです。打ち切りとは、観察対象についてイベントの発生時点を正確に観測できなかったケースを指します。打ち切りデータを単に除外してしまうと、イベントの発生までにかかる時間（生存時間）を過小評価することになり、統計的なバイアスが生じるおそれがあります。生存時間解析では、こうした打ち切りデータも情報として取り入れることで、より正確な分析を可能にしています。

例えば、サブスクリプション型サービスにおける「解約までの時間（＝生存時間）」を分析する際には、以下のようなデータ構造が考えられます。このデータには、各顧客がサービスを初めて利用した日（利用開始日）、実際に解約した日（解約日）、および追跡を終了した日（追跡終了日）が記録されています（追跡終了日は2025年3月31日を上限としています）。なお、追跡終了日までに解約が確認されなかった顧客（例：ID 1, 5）や、何らかの理由で途中で追跡ができなくなった顧客（例：ID 2）は、打ち切りデータとして扱います。

ID	利用開始日	解約日	追跡終了日	年齢	性別	地域	ログイン数
1	2020/4/12		2025/3/31	56	2	C	23
2	2020/9/27		2024/1/19	69	2	A	10
3	2021/12/1	2022/5/1	2022/5/1	46	1	B	20
4	2021/4/11	2022/8/12	2022/8/12	32	2	C	12
5	2021/5/6		2025/3/31	78	2	B	9
…	…	…	…	…	…	…	…
499	2020/6/9	2020/7/30	2020/7/30	56	1	A	16
500	2020/9/9	2022/4/22	2022/4/22	75	2	B	17

生存時間解析のビジネス活用例

スマホアプリのサブスクリプション解約につながる要因を探索する

この分析事例では、サブスクリプションサービスの解約リスクを把握するために、生存時間解析を用いてユーザーの継続傾向と影響因子を明らかにしました。

カプランマイヤー推定

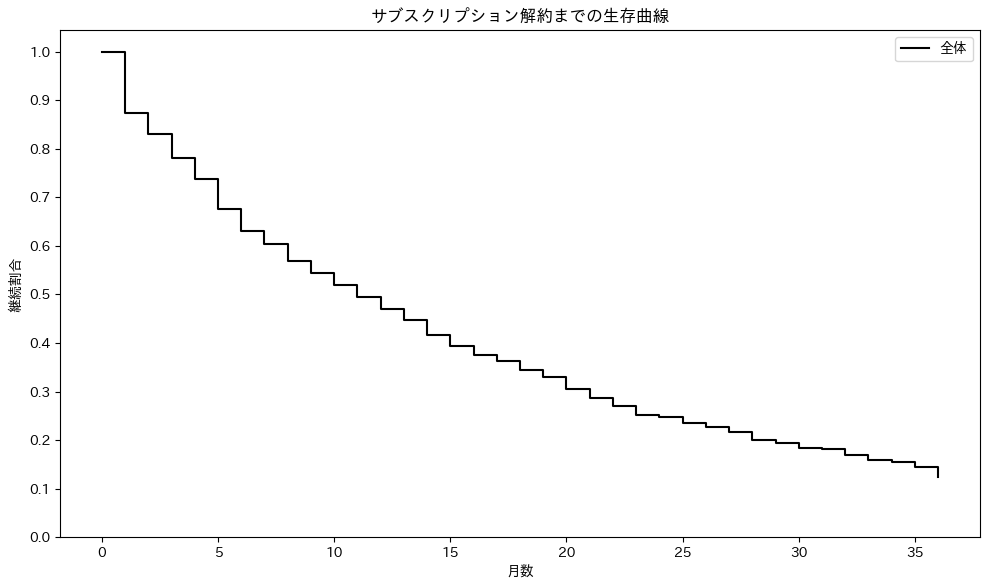
サブスクリプション解約をイベントとする生存時間データ（整形済み）を用意し、カプランマイヤー法を用いて生存関数を推定しプロットしてみます。この生存曲線は、サブスクリプションが解約されずに継続されている割合を月単位で表しています。※ここでは仮のデータを使用しています

ログランク検定

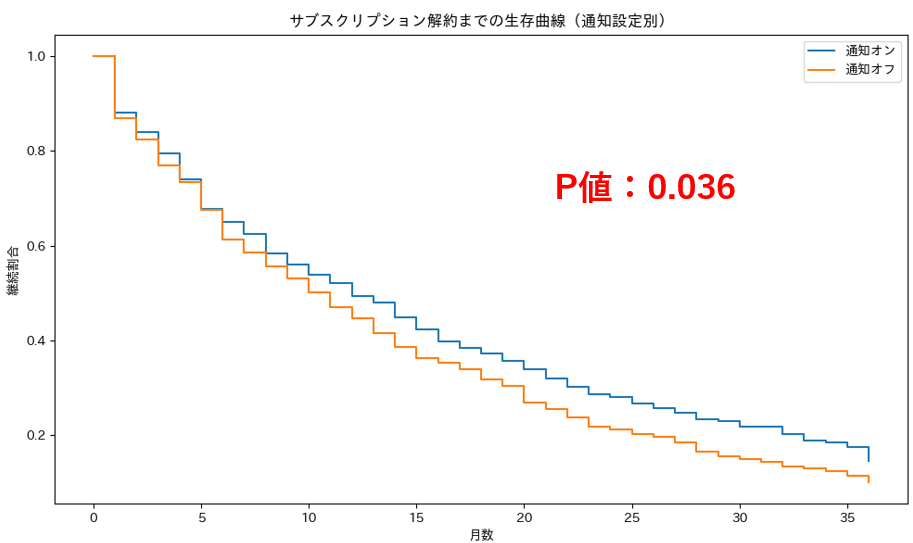
どんな会員が解約するのかを確認するために、ある因子でグループ分けを行い比較をします。例えば「アプリの通知オンにしているユーザー」と「アプリの通知オフにしているユーザー」に分けて生存曲線を描くことで、それぞれの継続傾向の違いを確認することができます。また、ログランク検定をおこなうことで、両グループの生存曲線に統計的な差があるかを確認することができます。今回の結果としては、p値が0.036のため統計的な差があるとがあると言うことができます（有意水準5％の場合）。

しかし、ログランク検定はあくまでも単一の因子でグループ分けを行い、そのグループ間で生存曲線に有意差があるかを検定する手法です。そのため他の因子の影響を考慮できないため、交絡の可能性がある場合などには正確な検定ができない可能性があります。そこで多変量解析であるCox回帰をおこなうことで、交絡も調整したうえで、説明変数がイベント発生リスクにどの程度関係しているかを数値として明らかにすることができます。

Cox回帰

今回は説明変数として、年齢、性別、アプリの使用頻度（直近1ヶ月間の平均起動回数）、通知設定（オン/オフ）、過去の課金額、満足度、フィードバック送信有無を使用してCox回帰を行います。

結果は以下のようになりました。

説明変数	回帰係数（β）	ハザード比（exp(β)）	p値
年齢	0.10	1.11	0.03
性別（男性:0, 女性:1）	0.09	1.09	0.09
アプリの使用頻度	-0.17	0.84	0.06
通知設定（オフ:0, オン:1）	-0.06	0.94	0.04
課金額	-0.03	0.97	0.02
満足度	-0.12	0.89	0.03
フィードバック送信（無し:0, 有り:1）	-0.01	0.99	0.10

以下のように読み取ることができます。

• p値より年齢、通知設定、課金額、満足度が統計的に有意
• 年齢が高いユーザーほど解約リスクが増加する
• 通知をオンにしているユーザーはオフに比べて解約リスクが低下する
• 課金額が多いユーザーほど解約リスクが低下する
• 満足度高いユーザーほど解約リスクが低下する

これらを踏まえると、若年層に向けた通知設計の最適化や、課金導線の整備、ユーザーフィードバックに基づく改善の徹底などの施策が有効と考えることができます。

その他の活用例

その他の業界における活用事例をご紹介します。
生存時間解析は業界を問わず活用されている汎用的な手法であり、ご自身のビジネスドメインでも応用できる可能性があります。

手法	マーケティング	医療	製造	金融	人事
分析対象	スマホアプリのサブスク	通院中の患者	製造機器	ローン契約者	従業員
目的変数	解約	入院	故障	債務不履行	退職
カプランマイヤー推定の狙い	サービス継続割合の推移	非入院継続割合の推移	稼働継続割合の推移	返済継続割合の推移	勤続割合の推移
ログランク検定の狙い	通知オン・オフで有意差があるか	服薬状況などで有意差があるか	メーカーの違いで有意差があるか	職業の違いでの有意差があるか	部署の違いで有意差があるか
COX回帰の狙い	説明変数 ・年齢 ・性別 ・通知設定 などが解約リスクに与える影響を推定	説明変数 ・年齢 ・既往歴 ・服薬状況 などが入院リスクに与える影響を推定	説明変数 ・工場内温度 ・過去生産量 ・メーカー などが故障リスクに与える影響を推定	説明変数 ・年齢 ・延滞履歴 ・職業 などが債務不履行リスクに与える影響を推定	説明変数 ・勤務拠点 ・勤務時間 ・部署 などが退職リスクに与える影響を推定

生存時間解析の注意点

ログランク検定結果の解釈

ログランク検定のp値は、サンプルサイズが大きいほど小さくなりやすく、統計的に有意になりやすいという特徴があります。そのため有意差が検出されたとしても、実務で活かせるほどの差であるとは限りません。

ログランク検定は生存曲線の全体的な違いを比較するものの、ハザード比などの効果量を提供しないため、結果の解釈には注意が必要です。実務的な判断をおこなうためには、ログランク検定と併せて、Cox回帰を用いてハザード比を算出し、リスクや影響の大きさを定量的に評価することが重要です。

交絡因子の調整

交絡因子とは、目的変数と説明変数の両方に関連し、両者の因果関係を歪める可能性のある変数のことをいいます。多変量解析において線形回帰モデルを用いる場合、交絡因子を適切に調整しないと正しく効果推定できない可能性があります。特にCox回帰では、打ち切りや観察期間の個体差といった時間に依存する複雑な構造を持つため、交絡因子の影響が結果に強く現れやすく慎重な調整が求められます。

交絡の調整方法としては、Cox回帰モデルの説明変数として交絡因子を含める方法のほか、傾向スコアマッチングなど因果推論の枠組みに基づくアプローチが挙げられます。

多重共線性の確認

Cox回帰といった線形回帰モデルでは多重共線性にも注意が必要です。多重共線性とは、説明変数同士の相関が高い状態を指し、この状態では各変数の効果（ハザード比）の推定が不安定になります。推定値の標準誤差が大きくなり、統計的に有意な差が検出されにくくなるほか、変数の解釈が困難になる恐れがあります。

多重共線性の回避については別記事にて説明していますので、そちらも合わせてご覧ください。

Cox回帰モデルの使い分け

時間とともに変化する説明変数があるなど、比例ハザード性が成り立たない場合、通常のCox回帰を用いると誤った推定結果を導く可能性があります。時間とともに変化する要因を適切に考慮するには時間依存性Cox回帰を、比例ハザード性が成り立たない場合には層別Cox回帰を用いるなど、状況に応じたモデル選択が重要です。

まとめ

生存時間解析は、イベント発生までの時間を分析する統計手法であり、打ち切りデータを考慮できる点が特徴です。シンプルな手法から高度なモデルまで幅広く活用でき、実務でも応用しやすく多様な分野で活用されています。適切なモデルを選択し、データの特性を踏まえて分析をおこなうことで、より深い知見を得ることができます。

生存時間解析の理解と実践に貢献できれば幸いです。

こちらもご覧ください