お気軽にお問い合わせください
データの特徴を把握できる相関係数と相関分析を徹底解説!

相関分析とは
相関分析は、二つのデータ間の関係性を表した数値(相関係数)を用いて分析する手法で、2変数間の特徴やデータ全体の傾向を理解するために広く利用されています。
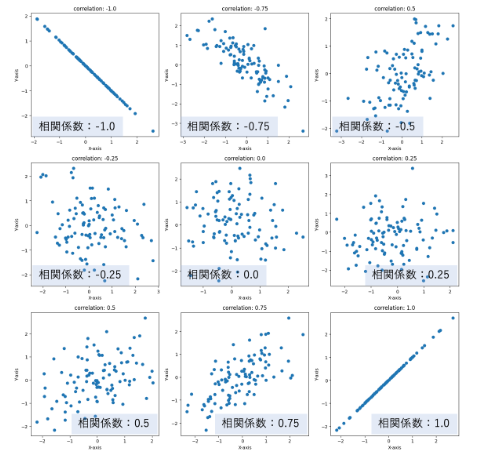
相関分析では、データ間の関係性を示す指標として相関係数を用います。相関係数は-1から1の範囲で値を取り、±1に近いほど強い相関、0に近いほど相関がほとんどないことを意味します。また、相関係数が正であれば正の相関、負であれば負の相関、0であれば無相関と呼ばれます。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。相関分析の実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
相関係数の種類
相関分析を実施するために相関係数を算出する必要があります。その相関係数には、データの種類や目的に応じてさまざまな種類があります。以下に主な相関係数を紹介します。
| 相関係数の種類 | 数式 | 変数の説明 | 取りうる範囲 | 現場の使用頻度 | 使用する場面 | 使用例 |
|---|---|---|---|---|---|---|
| ピアソンの積率相関係数 | $$\mathbf{r} = \frac{\mathrm{Cov}(\mathbf{X}, \mathbf{Y})}{\sigma_{\mathbf{X}} \cdot \sigma_{\mathbf{Y}}}$$ | ・\({Cov}(\mathbf{X}, \mathbf{Y})\) :変数\(X\)と\(Y\)の共分散 ・\(\sigma_{\mathbf{X}}\):変数\(X\)の標準偏差 ・\(\sigma_{\mathbf{Y}}\):変数\(Y\)の標準偏差 | -1 ~ 1 | ★★★★ (使用頻度非常に高い) | 量的変数同士の相関を測定する際に使用 | 売上高×広告費用 |
| 点双列相関係数 | $${r}_{\mathrm{pb}} = \frac{M_1 – M_0}{S} \cdot \sqrt{\frac{n_1 n_0}{n^2}}$$ | ・\(M_1\) :処置群の平均値 ・\(M_0\) :対照群の平均値 ・\(S\) :二つの群のデータの標準偏差 ・\(n_1\) :処置群のサンプルサイズ ・\(n_0\) :対照群のサンプルサイズ ・\(n\) :全体のサンプルサイズ | -1 ~ 1 | ★★★☆ (使用頻度高い) | 二項カテゴリ変数と量的変数の相関を測定する際に使用 | キャンペーン参加の有無×売上額 |
| 偏相関係数 | $${r}_{xy \cdot z} = \frac{\mathbf{r}_{xy} – \mathbf{r}_{xz} \mathbf{r}_{yz}}{\sqrt{\left(1 – \mathbf{r}_{xz}^2\right)\left(1 – \mathbf{r}_{yz}^2\right)}}$$ | ・\({r}_{xy}\) :\(x\)と\(y\)の相関係数 ・\({r}_{xz}\) :\(x\)と\(z\)の相関係数 ・\({r}_{yz}\) :\(y\)と\(z\)の相関係数 | -1 ~ 1 | ★★★☆ (使用頻度高い) | 他の変数の影響を除いた2変数間の相関を測定する際に使用 | 売上高×広告費 ※季節性を除外 |
| ファイ係数 | $${\phi}=\frac{{ad}-{bc}}{\sqrt{\left({a}+{b}\right)\left({c}+{d}\right)\left({a}+{c}\right)\left({b}+{d}\right)}}$$ | \(a\):キャンペーンに参加&購入 \(b\):キャンペーンに参加&未購入 \(c\):キャンペーンに不参加&購入 \(d\):キャンペーンに不参加&未購入 | 0 ~ 1 | ★★☆☆ (使用場面が限定的) | 二項カテゴリ変数同士の関連性を測定する際に使用 | キャンペーン参加の有無×購入有無 |
| クラメールのV | $${V}=\sqrt{\frac{{\chi}^{2}}{{n}\cdot{mi}{n}{\left({r}-{1},{c}-{1}\right)}}}$$ | ・\({\chi}^{2}\):カイ二乗値 ・\({n}\):サンプル数 ・\({r}\):列数(分割表の横軸のカテゴリ数) ・\({c}\):行数(分割表の縦軸のカテゴリ数) | 0 ~ 1 | ★★☆☆ (使用場面が限定的) | カテゴリ変数間の関連性を測定する際に使用 | 広告媒体の種類×購入意向 |
| ポリコリック相関係数 | 計算手順は複雑であり、手作業で行うのは困難。 そのため、統計ソフトウェアなどを用いて 計算することが多い。 | – | -1 ~ 1 | ★☆☆☆ (専門的または限定的) | 順序尺度の変数間の相関を測定する際に使用 | 顧客満足度評価×サービス品質評価 |
| スピアマンの順位相関係数 | $${r}_{s}={1}-\frac{{6}\sum{d}_{i}^{2}}{{n}\left({n}^{2}-{1}\right)}$$ | ・\({d}_{i}\):順位の差 ・\({n}\):サンプル数 | -1 ~ 1 | ★★★★ (使用頻度非常に高い) | 順位データの相関を測定する際に使用 | 顧客満足度×リピート購入の回数 |
| ケンドールの順位相関係数 | $${\tau}=\frac{\left({K}-{D}\right)}{\frac{{1}}{{2}}{n}\left({n}-{1}\right)}$$ | ・\({K}\):一致したペアの数(同じ順序のペア) ・\({D}\):不一致なペアの数(逆順序のペア) ・\({n}\):順位データの総数 | -1 ~ 1 | ★★★☆ (使用頻度高い) | 順位の一致度を測定する際に使用 | 製品の評価×顧客の再購入意向 |
| 級内相関係数 (ICC) | Case1:検者内信頼性 $$\hat{\rho}_1 = \frac{\text{MSB} – \text{MSE}}{\text{MSB} + (k – 1) \text{MSE}}$$ | ・\(\hat{\rho} : 級内相関係数\) ・\({MSB} : 被験者間平均平方\) ・\({MSE} : 誤差平均平方\) ・\( k : 測定者数\) | 0 ~ 1 | ★★☆☆ (使用場面が限定的) | 同じ対象に対して複数の測定が一致しているかを測定する際に使用 | 販売員×製品の評価 |
| Case2:検者間信頼性 $$\hat{\rho}_2 = \frac{\text{MSB} – \text{MSE}}{\text{MSB} + (k – 1) \text{MSE} + \frac{n}{k} (\text{MSW} – \text{MSE})}$$ | ・\(\hat{\rho} : 級内相関係数\) ・\({MSB} : 被験者間平均平方\) ・\({MSW} : 被験者内平均平方\) ・\({MSE} : 誤差平均平方\) ・\( n : 測定回数\) ・\( k : 測定者数\) | |||||
| Case3:絶対一致信頼性 $$\hat{\rho}_3 = \frac{\text{MSB} – \text{MSE}}{\text{MSB} + (k – 1) \text{MSE}}$$ ※式は case 1 と同様であるが,MSE の計算式が異なるので, 一般にcase 1 とは異なった値となります。 | ・\(\hat{\rho} : 級内相関係数\) ・\({MSB} : 被験者間平均平方\) ・\({MSE} : 誤差平均平方\) ・\( k : 測定者数\) |
量的変数(連続データ)間の相関
- ピアソンの積率相関係数
ピアソンの積率相関係数は、2つの連続変数間の線形関係を評価する指標です。
例えば、広告費用と売上高のような連続データにおいて、片方が増加するともう片方も増加する(または減少する)関係性を示します。
データが正規分布に近い場合や、線形関係が前提となる場合に適しています。
- 点双列相関係数
点双列相関係数は、1つの二値変数と1つの連続変数との相関を評価します。
例えば、キャンペーン参加の有無(0: 不参加, 1: 参加)と売上高の関係を測定します。
二値データが連続変数にどのような影響を与えるかを分析する際に適しています。
- 偏相関係数
偏相関係数は、他の変数の影響を取り除いた上で2つの変数間の相関を評価します。
見かけ上の相関が他の要因による間接的な影響である場合、この影響を排除し、2つの変数間の実際の関係を明らかにします。
例えば、広告費と売上高の相関が季節性要因に影響されている場合、偏相関係数を使うことで季節性の影響を排除し、広告費が売上高に与える直接的な影響を評価できます。
質的データ(カテゴリ・離散データ)間の相関
- ファイ係数
2×2の分割表(2つのカテゴリ変数間)の関連性を測定するために用いられる指標です。
例えば、商品Aの購入有無(購入: 1 / 未購入: 0)と商品Bの購入有無(購入: 1 / 非購入: 0)との関係を評価する際に使用されます。
データが二値データのみで構成される場合に適しています。
- クラメールのV
クラメールのVは、ファイ係数を一般化した指標で、2×2以上の分割表におけるカテゴリ変数間の関連性を評価します。
例えば、広告媒体の種類(例: テレビ, インターネット, チラシ)と購入意向(購入する/しない)との関係を測定する際に使用されます。
複数のカテゴリを持つ変数間の相関を評価する場合に適しています。
順位データ間の相関
- スピアマンの順位相関係数
スピアマンの順位相関係数は、データの順位に基づいて計算され、2つの変数間の相関関係を評価します。
例えば、顧客満足度(例えば「非常に満足」「満足」「普通」「不満」「非常に不満」などの順序尺度データ)と、リピート購入回数(数値化されたデータ)の関係性を確認するために使用します。この場合、顧客満足度の「非常に満足」「満足」などのカテゴリーを順位に変換し、それをリピート購入回数と関連付けて評価します。
特に、数値データが非線形である場合や外れ値が多い場合に適しています。
- ケンドールの順位相関係数
ケンドールの順位相関係数は、順位データ同士の一致度を評価する指標であり、ペアごとに「一致」と「不一致」を判定して、どの程度一致しているかを示します。
例えば、2つの順位データセット(例えば、顧客満足度の順位と商品評価の順位)において、どのペアが一致しているか(両方の順位が同じ方向に変動している)または不一致であるか(片方の順位が逆方向に変動している)を判定し、その一致度を測定します。
ケンドールの順位相関係数は、データの変動が小さく、順位間の不確実性が高い場合に適しています。
- ポリコリック相関係数
ポリコリック相関係数は、順序尺度データ同士の相関を評価するための指標です。
順序尺度データとは、例えば顧客満足度の「非常に満足」「満足」「普通」「不満」「非常に不満」など、順番に意味があるが、その間隔が均等でないデータのことです。このようなデータ同士の関連性を評価するために、ポリコリック相関係数を用います。ここで「間隔が均等でない」とは、「非常に満足」と「満足」の違いと、「満足」と「普通」の違いが、必ずしも等しいとは限らないことを意味します。
このようなデータの関連性を評価する際に、単純に「非常に満足」を5、「満足」を4、…「非常に不満」を1のように数値化して相関を求める方法では、各カテゴリ間の距離が等しいと仮定してしまうため、必ずしも適切な相関が得られないことがあります。ポリコリック相関係数では、このように単純に数値を割り当てるのではなく、各カテゴリの背後に連続的な変数があると仮定します。
例えば、顧客の満足度は本来0から100までの連続した値で表されるかもしれませんが、アンケートではそれを直接測定することができないため、「非常に満足」「満足」などのカテゴリに分けて記録されます。ポリコリック相関では、この連続的な満足度スコアが存在すると考え、そのスコアが一定の基準(閾値)で区切られた結果として、観測されたカテゴリが生じたとみなします。
このように、各カテゴリの間に潜在的な連続変数があり、それが閾値によって区切られていると仮定することで、より適切な相関を推定するのがポリコリック相関の考え方です。
ポリコリック相関は特に、カテゴリーの数が多い順序尺度データ(例:顧客満足度)間の相関分析に適しています。
計算手順は複雑であり、手作業でおこなうのは困難です。そのため、通常は統計ソフトウェアやプログラミング言語のライブラリを使用して計算します。具体的には以下の手順となります。
- クロス集計表の作成:
2つの順序尺度変数の観測データから、各カテゴリの組み合わせによる度数をまとめたクロス集計表を作成します。 - 閾値の推定:
各順序カテゴリが、潜在的な連続変数のどの範囲に対応するかを示す閾値を、累積相対度数と標準正規分布の逆累積分布関数を用いて推定します。 - 相関係数の最尤推定:
推定された閾値とクロス集計表の度数データを用いて、潜在変数間の相関係数を最尤法により推定します。具体的には、二変量正規分布の累積分布関数を用いて、観測データが得られる確率(尤度)を最大化する相関係数を求めます。
一致度や一貫性の測定
- 級内相関係数 (ICC)
級内相関係数 (ICC) は、同じグループ内での一致度を評価する指標です。
主に繰り返し測定データや複数の観測者が行った評価の一貫性を測定する際に使用されます。
例えば、医療診断において複数の医師が同一の患者に対して診断を行った場合、その診断結果の一致度を評価する際や、複数の実験者が同じ試料を測定した場合に得られる結果の一貫性を調べる際に使用されます。
特に、評価の一貫性や信頼性が重要な場面で適用されます。
ICCにはいくつかの種類があり、異なる計算方法が用いられます。代表的な3つのケースを以下に示します。
- Case 1: 検者内信頼性(単一測定の一貫性)
検者(観測者)ごとの測定の一貫性を評価する際に使用されるICCで、以下の式で計算されます。
$$\hat{\rho}_1 = \frac{\text{MSB} – \text{MSE}}{\text{MSB} + (k – 1) \text{MSE}}$$
・\(\hat{\rho} : 級内相関係数\)
・\({MSB} : 被験者間平均平方(被験者ごとの平均値のばらつき)\)
・\({MSE} : 誤差平均平方(測定誤差のばらつき)\)
・\( k : 測定者数\) - Case 2: 検者間信頼性(異なる測定者間の一致性)
異なる測定者間での評価の一致度を測るICCで、以下の式が用いられます。
この式では、MSWからMSEを差し引いた項が追加されており、異なる測定者によるばらつきが考慮される点が特徴です。
$$\hat{\rho}_2 = \frac{\text{MSB} – \text{MSE}}{\text{MSB} + (k – 1) \text{MSE} + \frac{n}{k} (\text{MSW} – \text{MSE})}$$
・\({MSW} : 被験者内平均平方(測定者間のばらつき)\)
・\( n : 測定回数\) - Case 3: 絶対一致信頼性(評価の絶対的な一致)
測定結果が絶対的に一致するかどうかを評価するためのICCで、以下の式が使用されます。
この式はCase 1と同じ形ですが、MSEの計算方法が異なるため、一般に異なる値となります。
$$\hat{\rho}_3 = \frac{\text{MSB} – \text{MSE}}{\text{MSB} + (k – 1) \text{MSE}}$$
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。相関分析の実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
相関分析によってわかること
変数間の関係性
相関係数は2変数の関係性を明らかにします。例えば、商品の売上と広告費用の相関係数を算出することで、広告投資が売上に与える影響を理解することが可能です。相関係数の算出を各変数同士に広げて相関分析を実施することで、その結果を基に、回帰分析や機械学習モデルに使う変数を選択する際の根拠のひとつとする場合があります。
相関係数による客観的評価
相関係数は、2つの変数間の関連性の強さと関係が正の相関(増加する)か負の相関(減少する)かを示す指標です。相関係数が+1に近い場合は強い正の相関を示し、-1に近い場合は強い負の相関を示します。
ただし、相関がどの程度強いと判断するかの基準は、分析の分野やドメインによって異なります。そのため、相関係数の値を個別に評価するだけでなく、複数の変数間で比較し、「この変数間の相関係数の方が大きいため、より強い相関関係がある」といった相対的な判断も重要になります。
ビジュアル化による洞察
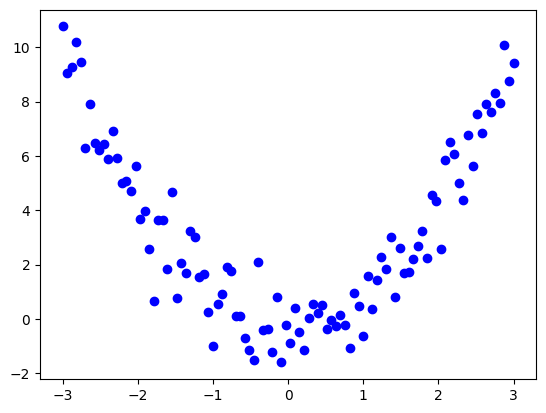
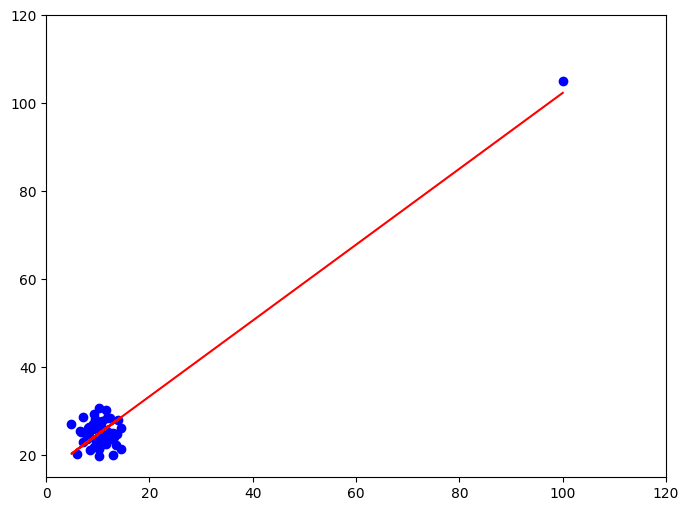
相関分析では、相関係数だけでなく散布図による可視化が重要です。相関係数は線形な関係しか捉えられず、非線形な関係や外れ値の影響を見落とす可能性があるからです。
例えば、上図のように曲線的な関係があっても相関係数は低い値(-0.02)を示し、下図のように外れ値によって相関係数が高く(0.96)見えてしまうことがあります。散布図を用いることで、データ全体の傾向や外れ値の有無を視覚的に把握し、相関係数だけでは見抜けない関係性や異常を発見できます。
ビジネス活用例
活用例① 企業好感度に影響している要因の特定
ビジネスにおいて、企業好感度のような重要指標に影響を与える要因を特定するためには、相関分析、主成分分析、回帰分析などの統計手法を組み合わせることが有効です。相関分析は、各指標間の関係性を把握するだけでなく、回帰分析の変数選択にも役立ちます。以下にその活用例を解説します。
データの概要は以下になります。
・企業好感度のデータ
・各媒体の広告費データ
・各SNSに関するデータ(フォロワー数、いいね数など)
・自社WEBサイトに関するデータ(ユーザー数、セッション数、ページ閲覧数など)
データの収集・整形のフェーズでは各媒体からデータを取得し、欠損値の処理やデータの粒度の統一などの前処理を行い、分析に適した形式に整えます。今回使用する指標は278項目です。
このフェーズで整形を行った後のデータ例は以下です。
| 企業好感度 | テレビ_広告費_ALL | WEB_広告費_ALL | 新聞_広告費_ALL | ・・・ |
|---|---|---|---|---|
| 41.7% | 15,180 | 8,574 | 101,115 | ・・・ |
| 42.2% | 49,433 | 7,950 | 29,899 | ・・・ |
| 42.3% | 31,170 | 3,743 | 35,547 | ・・・ |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
次に相関分析を実施します。まず、指標間のヒートマップを作成し、全体的な傾向を把握します。
色の濃さは相関の強さを示し、青が濃いほど正の相関が強く、赤が濃いほど負の相関が強いことを意味します。相関係数が一定の閾値(例:0.3以上)を満たす指標を重点的に確認し、強い相関が見られる指標を抽出します。
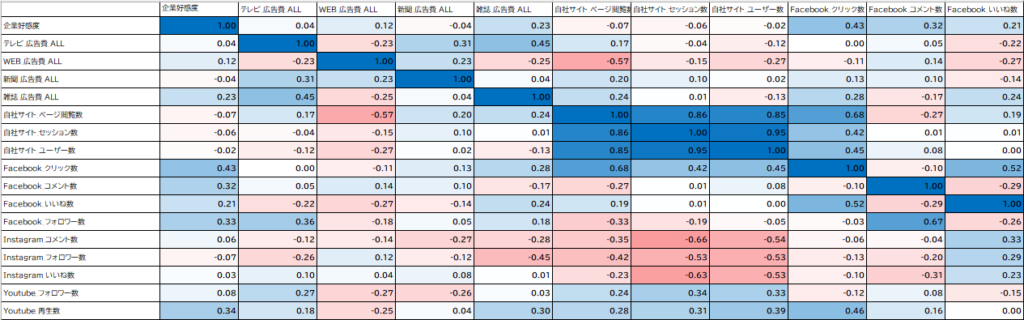
次に、企業好感度との相関を個別に確認します。特に、業界標準とされる指標について、相関の強さだけでなく、ビジネス上の妥当性も考慮しながら評価をおこないます。
また、相関が高い指標同士の多重共線性のリスクも考慮した上で、変数選択をおこないます。
算出した指標を基に、重回帰分析で使用する変数を選定します。選んだ変数を使って重回帰分析をおこない、各変数のP値やモデルの決定係数を評価しながら、最適な変数を選択します。さらに、必要に応じて主成分分析やLASSO回帰などの手法を活用し、変数を最適化し、モデルの精度向上を図ります。

当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。相関分析の実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
そのほかのビジネス活用事例
活用例② マーケティング戦略の最適化(マーケティング活動×売上)
マーケティング活動と売上の相関関係を分析することで、特定のマーケティング戦略が売上に与える影響を評価できます。
例えば、新しいデジタル広告を展開した際、広告費に加えて、SNSのインプレッション数やサイトの閲覧数など、他のマーケティング活動に関連するデータも収集します。その後、これらの要因と売上の相関係数を算出することで、マーケティング活動の効果を総合的に評価できます。高い相関が見られた場合、広告戦略やSNS活動、サイト運営などが売上に与える影響を示唆することができ、今後のマーケティング予算の配分や戦略の見直しに活かすことが可能になります。
活用例③ 製品開発と顧客ニーズ(顧客フィードバック×製品機能)
顧客からのフィードバックとアプリ機能の利用状況との相関を分析することで、どの機能が顧客満足度に寄与しているかを把握できます。
例えば、モバイルアプリのアップデート後に顧客満足度調査を実施し、アンケート結果とアプリ内での機能利用データを組み合わせて分析した結果、「利便性に関する満足度」と「プッシュ通知機能の活用頻度」の相関係数が0.68という強い正の相関が確認されました。この結果から、プッシュ通知機能を積極的に活用しているユーザーほど、アプリの利便性に高い満足感を持っていることが示唆されます。
相関分析の結果を踏まえて、プッシュ通知のパーソナライズ化や通知タイミングの最適化を図ることで、さらなる顧客満足度の向上が期待できます。
相関分析の注意点
ピアソンの積率相関係数を使用する際の前提条件
現場で使用する頻度が高いピアソンの積率相関係数は、2つの連続変数間の線形関係を測定するための指標であり、この指標を使用する際にはいくつかの前提条件があります。
- 線形性
ピアソンの相関係数は、変数間に線形な関係があることを前提としています。非線形な関係が存在すると、相関係数が誤解を招く結果となる可能性があります。したがって、データを分析する前に散布図などで線形性を確認することが重要です。 - 外れ値の影響
データに外れ値が含まれている場合も注意が必要です。外れ値は相関係数に大きな影響を与え、実際のデータ間の関係性を過大評価または過小評価する原因となります。このような場合、外れ値を削除するか、外れ値や分布の偏りに対して頑健なスピアマン順位相関係数やケンドール順位相関係数といった手法を使用することが適しています。 - 正規分布
ピアソンの相関係数は、データが正規分布に従う場合に最も信頼性が高いです。データが偏っていたり異常値が多い場合には、結果が歪む可能性があります。このような場合には対数変換や正規化などをおこない、データを正規分布に近づけることや、他の相関手法(スピアマン順位相関係数やケンドール順位相関係数)を使用することが推奨されます。
相関は因果関係を示す指標ではない
相関係数が高くても、1つの変数がもう1つの変数に影響を及ぼす原因であるとは限りません。
第三の要因(潜在変数)の影響や偶然の一致による場合もあります。
相関分析をおこなう際には、因果関係を安易に推測せず、結果に影響を及ぼしていると考えられる他の要因を検討する必要があります。
さらに、相関分析だけでは不十分な場合が多いため、他の分析手法も併用して多角的にデータを検討することが重要です。例えば、回帰分析を用いることで、特定の要因がどれだけ結果に寄与しているかを定量的に評価できます。また、因子分析を使えば、複数の変数間の関係性をより深く理解することが可能です。
サンプルサイズ
サンプルサイズが小さいと、ランダムな変動や外れ値の影響を受けやすく、相関係数が実際の関係を正しく反映しないことがあります。
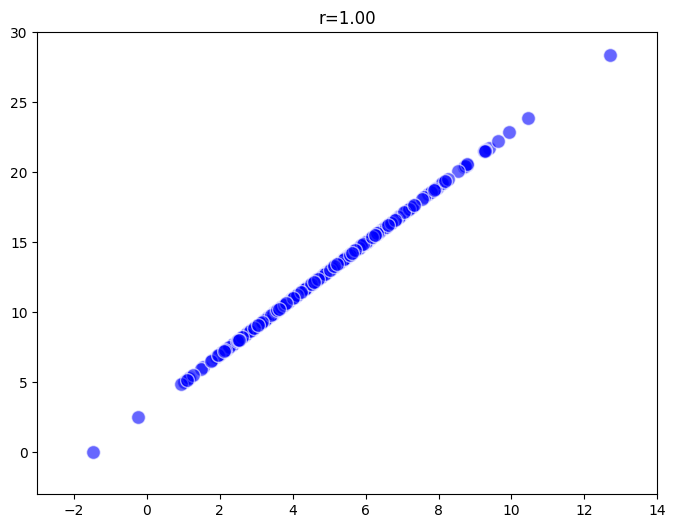
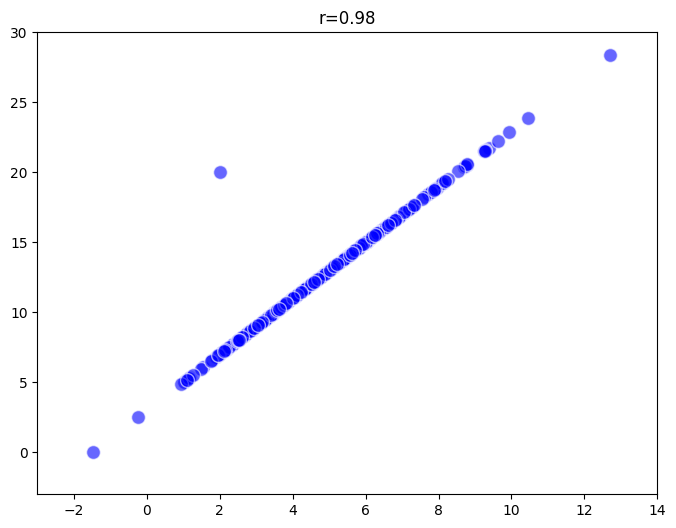
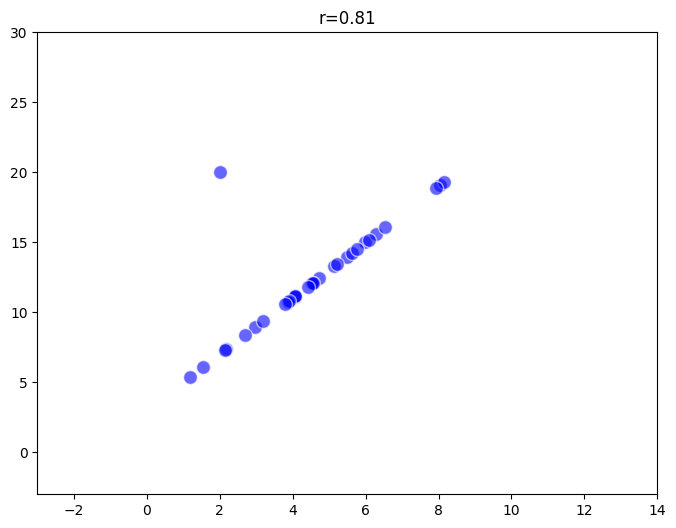
例えば、サンプルサイズが300の場合、左側の散布図ではデータが一直線に並んでおり、相関係数は1です。しかし、真ん中の散布図もサンプルサイズ300ですが、1つの外れ値が存在し、その結果相関係数は0.98にわずかに減少しています。右側の散布図ではサンプルサイズが30で、同様に1つの外れ値があるため、相関係数は0.81にまで低下しています。このように、サンプルサイズが小さいと外れ値の影響が大きくなるため、適切なサンプルサイズを確保することが重要です。
指標数が多い場合、結果の解釈に苦労する
相関分析では、指標(変数)の数が多いほど、結果の解釈が難しくなります。
例えば、10個の指標を分析する場合、相関係数の組み合わせは45通りですが、20個の指標では190通り、30個では435通りに増加します。このように相関係数の組み合わせが膨大になると、計算負荷が増し、結果の確認にも時間がかかります。
したがって、指標数が多い場合には以下のような工夫をおこなうことが重要です。
① 仮説を立てた上で分析を行う
事前に仮説を設定することで、分析対象となる変数を絞り込み、重要な関係性を特定しやすくなります。
②次元削減手法を活用する
必要に応じて主成分分析や因子分析などの次元削減手法を用いることで、多数の変数を少数の要因にまとめることができるため、それぞれの相関係数を確認する回数を減らすことができます。
これらの工夫を通じて、相関分析の有効性を高めることができます
欠損値の補完
データに欠損値が存在する場合、その補完方法は相関係数の値や解釈に大きく影響を及ぼす可能性があります。
欠損値への対処法としては、欠損値を含むレコードを削除する(リストワイズ削除)、平均値や中央値で補完する、回帰補完をおこなう、多重代入法(Multiple Imputation)を適用するなど、さまざまな手法が存在します。
重要なのは、分析者が欠損値の発生メカニズムを理解し、適切な補完方法を選択することです。
例えば、MCAR(Missing Completely at Random)は、欠損が観測変数や未観測変数に依存せず、完全にランダムに発生する場合を指します。この場合、リストワイズ削除によるバイアスは小さいと考えられます。
一方で、欠損が他の観測変数に依存して発生する場合(MAR: Missing at Random)、単純な平均値補完やリストワイズ削除は、推定値の歪みを引き起こす可能性があります。こうした場合、多重代入法を用いることで、より適切な推定値を得られる可能性があります。
分析結果を解釈する際には、どのような補完方法が用いられたのか、そしてその方法が結果に与える潜在的な影響について十分に考慮する必要があります。可能であれば、異なる補完方法を適用し、それぞれの相関係数の変化を比較検討することで、分析結果がどの程度安定しているか(補完方法によって大きく変わらないか)を確認し、関係者間で合意することが望ましいです。
まとめ
今回は相関分析について解説しました。
相関分析は、2つの変数間の関係性を数値で表し、データの傾向を把握するのに役立つ手法です。適切な相関係数を選択することで、より正確な分析が可能になります。
一方で注意点として、相関関係が因果関係を示すわけではないことがあり、その解釈には注意が必要です。また、データの分布や外れ値の影響を考慮することも重要です。
相関分析を適切に活用し、データの理解を深める一助となれば幸いです。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。相関分析の実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
こちらもご覧ください