Index
1. はじめに
データソリューション事業部の関田です。
日常やビジネスにおいて、巡回セールスマン問題やナップサック問題、そして最大カット問題に代表される組合せ最適化の課題は溢れています。イジングマシンを用いることは組合せ最適化問題を解くために最も効果的な方法の一つとして知られ、実際に多くの現場で使用されています。ここでは、イジングマシンで組合せ最適化問題を解くために必要な定式化の手法について解説します。
(余談)
2023/10/02に、mRNAワクチンの作成に関する研究に対してノーベル生理学・医学賞が与えられました。この研究に端を発し、新型コロナウイルスに対するワクチンをはじめとするmRNAワクチンの作成が可能となり、多くの命を救っています。
このような創薬の分野でも組合せ最適化は課題となっています。例えば、mRNAワクチンが生体内で安定に存在するために、RNA配列を最適化する研究が数多くなされています。もし興味があれば次の論文を読んでみてください。
論文:RNA folding using quantum computers (Fox DM, MacDermaid CM, Schreij AMA, Zwierzyna M, Walker RC (2022) )
この論文ではRNAの最適化だけでなく定式化の手法についても詳しく説明されており、定式化の勉強としてとても参考になります。
2. イジングマシンとは
イジングマシンとは量子コンピュータの一種であり、組合せ最適化問題を解くことに特化したマシンです。ただし、必ずしも最適解を出せるとは限りません。求解のアルゴリズムが確率的な処理を含むため、基本的には近似解を出します。
なお、イジングマシンという呼び方には流派がありますが、ここではアニーリング型量子コンピュータと疑似量子コンピュータのことをまとめてイジングマシンと呼ぶことにします。これらの大きな違いはマシンやアルゴリズムの中で量子技術を用いているか否かであり、人間が使用する際に行う定式化は同様です。
3. イジングマシンのための定式化
イジングマシンで組合せ最適化問題を解く際、問題を特定の形式で定式化する必要があります。そのような定式化手法は主に2つあり、それぞれイジングモデル、QUBO形式と呼ばれます。
いずれの手法にせよ、定式化でやるべきことは2値変数の2次多項式でハミルトニアン(目的関数)を定義することです。イジングマシンはハミルトニアンの最小値(最大値)を探索するので、最適解でハミルトニアンが最小(最大)となるように定式化しましょう。具体的な方法はこの後紹介します。
イジングマシンとQUBO形式の特徴は表1の通りです。
表1. イジングモデルとQUBO形式の特徴
| 定式化手法 | 2値の値 | よく変数に用いられる文字 |
|---|---|---|
| イジングモデル | \(\{-1, 1\}\) | \(\sigma_i\) |
| QUBO形式 | \(\{0, 1\}\) | \(q_i\) |
以下でも通例に則り、イジングモデルの変数を\(\sigma_i\)、QUBO形式の変数を\(q_i\) と書くことにします。
なお、添え字の\(i\) は \(i\) 番目の変数であることを意味します。
それでは、2つの定式化について詳しく見ていきましょう。
3.1. イジングモデル
まずは、イジングモデルという物理学における理論模型について簡単に紹介します。
\(n\)次元イジングモデルとは、\(n\)次元に整列したスピン状態からなる系です。
主な特徴は次の2つで、非常にシンプルです。
- 各スピンは\(\{-1, 1\}\)のいずれかの値を取る
- 考慮される相互作用は、2つのスピン同士の相互作用および1つのスピンと外部磁場との相互作用のみ
これらの特徴をもとに、系のハミルトニアンが定義されます。

ここで「各スピンがどちらの値を取れば、系のハミルトニアンが最小になるのか」ということに興味を持ってみましょう。つまり、系の基底状態を求めることを考えます。
2値(スピン)の状態からなるシステムの基底状態を求めるというのは、言い換えれば最適なスピンの組み合わせを求めるということです。まさに組合せ最適化問題を解こうとしていますね。
イジングモデルにおける定式化
一般に、イジングモデルのハミルトニアン\(H\)は次のように表されます。
\[H(\sigma) = \sum_{i,j} J_{i,j} \sigma_i \sigma_j + \sum_i h_i \sigma_i\]
ここで、\(J_{i,j}\) は \(i\) 番目と \(j\) 番目のスピンの相互作用、 \(h_i\) は \(i\) 番目のスピンに作用する外部磁場を表します。物理学でのイジングモデルに倣って相互作用や外部磁場という言い方をされますが、単純にそれぞれ2次、1次の項の係数です。
このような形で定式化するためには、スピンで表す対象と係数の値を決め、付随する制約条件も含めて2次式に落とし込む必要があります。制約条件をハミルトニアンとは別で表現して解くことはできません。
なお、これはあくまで一般的な形であり、必ずしも全く同じ形で書く必要はありません。肝心なのは、2値変数の2次多項式で書くことです。
3.2. QUBO形式
QUBOとは、Quadratic Unconstrained Binary Optimizationの略です。Unconstrainedとありますが、これは制約が無い問題しか解けないということではなく、イジングモデル同様、制約条件を2次式で表現しなくてはならないということです。
QUBO形式のハミルトニアンは次のように表されます。
\[H(q) = \sum_{i,j} Q_{i,j} q_i q_j + \sum_i b_i q_i\]
お気づきになったでしょうか。文字が異なるだけで、イジングモデルと全く同じ表現です。
3.3. 定式化の違い
2つの定式化を紹介しましたが、これらに違いはあるのでしょうか。結論を述べますと、数学的に違いは無く、人間が表現・解釈しやすいかどうかのみ異なります。
数学的等価性
各形式の数学的な等価性については、付録にて解説します。興味があれば是非ご覧ください。
人間による解釈性
イジングモデルとQUBO形式では変数の取る値が異なります。これによって、ハミルトニアンの各項(\(J_{i,j}\sigma_i \sigma_j\) など)には次のような違いが表れます。
表2. イジングモデルとQUBO形式でのハミルトニアンの各項の値について
| 定式化手法 | 変数の値 | ハミルトニアンの各項の絶対値 | ハミルトニアンの各項の符号 |
|---|---|---|---|
| イジングモデル | \(\sigma_i \in \{-1, 1\}\) | 変数に依存しない (係数の絶対値に等しい) |
変数に依存する |
| QUBO形式 | \(q_i \in \{0, 1\}\) | 変数に依存する (変数の少なくとも1つが0ならば0、 変数が共に1ならば係数の絶対値に等しい) |
変数に依存しない (係数の符号に等しい) |
解釈性の違いによる定式化の使い分け関して、筆者が個人的に最も大事だと思うポイントはすべての変数を考慮して変数間の相互関係を見たいか、変数の取捨選択をしたいかです。
つまり、以下のように使い分けます。
- イジングモデル:変数同士の関連性などを考慮してすべての対象を分類するような問題
- QUBO形式:ある位置にある変数を割り当てるか否か、つまり取捨選択を考えることで、変数の順序や配置を考える問題
この点に注目し、イジングモデルとQUBO形式のどちらを用いると良いのかを、例題を用いて考えていきます。
4. 例題
最大カット問題
最大カット問題とは、互いに関連のある複数のデータを、関連性に応じて適切に二分する問題です。
具体的に次の問題を考えてみます。
設定:
4人でサッカー対戦を行う。集まった4人には、図2の通りポジションが割り当てられている。
問題:
次の条件をなるべく満たすようにチーム分けを行う。
条件:
・チーム内でポジションが偏らないようにする
・各チームの人数が平等になるようにする
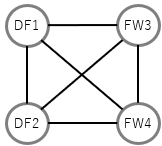
では考えていきましょう。
1. イジングモデル or QUBO形式
すべての変数を考慮して変数間の相互関係を見たいか、変数の取捨選択をしたいか
この問題では変数を選手に割り当てます。そして、ある選手とそのチームメイトとのポジションの関係性やチーム内の人数を考慮して最適な分類を行う必要があります。この考え方に基づくと、イジングモデルで定式化すると良さそうです。
2. イジングモデルへの落とし込み
変数 \(\sigma_i\) が\(\{ -1, 1 \}\) のどちらの値を取るかによって、\(i\) 番の選手がどちらのチームに入るかが決まるという解釈をすることにします(例えば、-1ならAチーム、1ならBチーム)。そのもとで、変数(選手)同士の相互作用を考えます。
今回の場合、相互作用を決めるにあたって考慮する点はポジションとチームの人数の2つです。
ポジション
先ほど \(\sigma_i\) という変数を用意しましたが、ポジションを考慮するために、ポジションを表す係数として \(p_i\) を導入します。\(p_i\) はDFなら \(1\)、FWなら \(-1\) の値を取るということに決めておきます。つまり、\(p_i\) は変数ではないことに注意が必要です。
異なるポジションの選手と同じチームになる状況でハミルトニアンが小さく、同じポジションの選手と同じチームになる状況でハミルトニアンが大きくなるようにします。
これを満たすためには、\(i\) 番と \(j\) 番の選手に関して、相互作用項 \(J p_i p_j \sigma_i \sigma_j\) を考えればよいです。ここで、相互作用の係数 \(J\) は下表の通り、正の数に設定すればよいことがわかります。
表3. ポジションに関する相互作用項の係数の符号
| \(i\)番と\(j\)番のチーム | \(i\)番と\(j\)番のポジション | \(\sigma_i \sigma_jの値\) | \(p_i p_jの値\) | \(p_i p_j \sigma_i \sigma_jの値\) | 相互作用の係数の符号 |
|---|---|---|---|---|---|
| 同じ | 同じ | 1 | 1 | 1 | 正 |
| 同じ | 異なる | 1 | -1 | -1 | 正 |
| 異なる | 同じ | -1 | 1 | -1 | 正 |
| 異なる | 異なる | -1 | -1 | 1 | 正 |
このように、今回の場合は相互作用の係数は常に正にすれば良いです。具体的な値に関しては、適宜チューニングして決める必要があります。結局、ポジションに関するハミルトニアンは次の式で書くことができます。
\[H_p = \sum_{i,j} J p_i p_j \sigma_i \sigma_j\]
人数
4人で2チームに分かれるので、理想的な配分は各チーム2人です。2人ずつに分かれている際、4変数が取っている値は \(\{-1, -1, 1, 1 \}\) です。つまり、4変数の和が0になっています。逆に2人ずつに分かれていない場合は、和が0にはならず、不均等な分かれ方をしているほど0から遠ざかります。
このように、ある基準値からの離れ具合の表し方は次の通りです。
\[H_n = a\Bigl(\sum_i \sigma_i – 0\Bigr)^2\]
「基準値からの離れ具合」を表す際、基準値との大小関係は無関係であり、符号が変わってはいけないので2乗します。また、今回は基準値が0なので敢えて書く必要はありませんが、基準値が0でない場合は、0の代わりにその基準値を用いてください。\(a\) は適当な正の係数です。
3. 全体のハミルトニアン
以上をまとめることで、最小化したいハミルトニアンが次式で表されます。
\[\begin{align} H(\sigma) &= H_p + H_n \\ &= \sum_{i, j} J p_i p_j \sigma_i \sigma_j + a\Bigl(\sum_i \sigma_i \Bigr)^2 \end{align}\]
4. 解いてみる
まずは、係数 \(J, a\) を1にしてみます。このときハミルトニアンを最小にする最適解は
\((\sigma_1, \sigma_2, \sigma_3, \sigma_4) = (1, -1, 1, -1), (1, -1, -1, 1), (-1, 1, -1, 1), (-1, 1, 1, -1)\)
の4通りです。
もし間違えて、\(a=-1\)にしてしまったらどうなるでしょうか。\(a<0\) の場合、チームの人数に偏りがあるほど \(H_n\) は小さくなるため最適解が変わり、
\[\{\sigma_1, \sigma_2, \sigma_3, \sigma_4\} = \{-1, -1, -1, -1\}\ \rm{or}\ \{1, 1, 1, 1\}\]
となってしまいます。これでは全員が同じチームに入り、試合になりません。
5. 【再考】イジングモデル or QUBO形式
すべての変数を考慮して変数間の相互関係を見たいか、変数の取捨選択をしたいか
先ほどは「相互関係を考えて、各選手をいずれかのチームに割り振る」という考えのもとイジングモデルで定式化する立場を取りましたが、他の考え方をしてみます。
2チームをそれぞれA, Bとすると「各選手がAチームに入るか否か」で分けることができます。この考え方では「Aチームに入る選手を選ぶ」という取捨選択をするので、QUBO形式で定式化することもできます。つまり、Aチームに入る選手には1、Aチームに入らない(Bチームに入る)選手には0を割り当てます。
具体的な定式化は省略しますが、是非イジングモデルと同様に考えてみてください。
今回は単純な問題設定にしたため、コンピュータを使わずとも最適解が求められますし、係数のチューニングもあまり必要ありませんでした。しかし問題が複雑になるほど、定式化してイジングマシンに解かせて係数のチューニングをしてまた解かせて、、、という繰り返しが必要になります。
組合せ最適化の例題はネットや本でたくさん見ることができるので、是非練習してみてください。また本記事の例題は私が自作したものですが、このように簡単な問題を作って解くことも良い練習になると思います。
おわりに
本記事では、組合せ最適化問題をイジングマシンで解く際の定式化について、例題を用いて解説しました。
イジングマシシンの定式化では2値の2次式で表現しなくてはなりませんが、工夫によって様々な問題を解くことができます。
日常やビジネスの世界でありふれる組合せ最適化問題を、イジングマシンで解決してみましょう!
付録
A.1. 定式化の数学的等価性
次の変換を施すことにより、イジングモデル \(\sigma_i \in \lbrace -1, 1 \rbrace\) をQUBO形式 \(q_i \in \lbrace 0, 1 \rbrace\) で表すことができます。
\[\sigma_i = 2q_i-1\]
確認してみましょう。
\[\begin{align} H(\sigma) &= \sum_{i,j} J_{i,j} \sigma_i \sigma_j \ + \sum_i h_i \sigma_i \\ &= \sum_{i,j} J_{i,j}(2q_i-1)(2q_j-1) + \sum_i h_i(2q_i-1) \\ &= \sum_{i,j} 4J_{i,j}q_iq_j + \sum_i 2h_iq_i + \sum_{i,j} (-2J_{i,j})(q_i + q_j) + \sum_i(-h_i) \\ &= \sum_{i,j} Q_{i,j}q_iq_j + \sum_i 2h_iq_i + \sum_i (-4J’_iq_i) + A \\ &= \sum_{i,j} Q_{i,j}q_iq_j + \sum_i b_i q_i + A \\ &= H(q) \end{align}\]
ここで、3行目から4行目の変換では、
\[\begin{align} 4J_{i,j} &= Q_{i,j}, \\ \sum_j J_{i,j} &= J’_i, \\ \sum_i (-h_i) &= A = \rm{const.} \end{align}\]
とし、4行目から5行目の変換では、
\[2h_i-4J’_i = b_i\]
としています。これで示すことができました。
なお、定数項はハミルトニアンを最小にする基底状態に影響を与えないので、定数項の有無は解の探索に無関係です。したがって \(A\) が残っていても問題ありません。
イジングモデルとQUBO形式の関係について述べましたが、さらに言えば、特に名前の付いていない任意の定式化が可能です。例えば、
\[x_i = 7q_i-2\]
なる変換により、\(q_i \in \lbrace 0, 1 \rbrace\) を \(x_i \in \lbrace -2, 5 \rbrace\) で表すことができます。
A.2. 定式化ごとの解釈性
\(x_i \in \lbrace -2, 5 \rbrace\) のように任意の二値変数を用いて定式化することが可能であることを説明しました。
ただし、一般的には-2と5を単位として2値表現すると定式化を複雑にし、解釈性に乏しくなります。
その理由の一例は、ハミルトニアンの各項の係数比が単純にハミルトニアンへの影響度の比ではなくなってしまうことです。つまり、項の絶対値を決める要因が、係数以外に \(x_i\) の絶対値にも関係してしまうことです。
それに対してイジングモデルやQUBO形式では、変数が取りうる値が \(0\) や \(\pm1\) なので、各項の絶対値は変数の値に応じて0または係数の絶対値になります。したがって「影響が大きい項の係数の絶対値は大きく、影響が小さい項の係数の絶対値は小さくする」という単純な定式化ができます。また、すでに定式化されたハミルトニアンを読む際にも、係数に注目すれば項の重要度が分かります。
このような理由があるので、基本的にはイジングモデルかQUBO形式で定式化すれば良いでしょう。
参考
- 基礎から学ぶ量子コンピューティング-イジングマシンの仕組みを中心に- (株式会社オーム社、工藤和恵)
- Fox DM, MacDermaid CM, Schreij AMA, Zwierzyna M, Walker RC (2022) RNA folding using quantum computers. PLoS Comput Biol 18(4): e1010032. https://doi.org/10.1371/journal.pcbi.1010032
- イジングマシン活用アプリケーションの開発を支援するコンピューティングシステム(NTTコンピュータ&データサイエンス研究所)
