「0,1判別」の定番手法！ロジスティック回帰分析とは？

「ロジスティック回帰分析」は、「製造業における故障の発生有無」や「オンラインサービスにおける顧客の離脱の発生有無」など「0」か「1」を予測する「2値分類」のタスクで活用される分析手法の一つです。
特定の事象が発生する確率を推計する手法なので、ビジネスシーンでも活用しやすい分析手法といえます。

本記事では、このロジスティック回帰分析の考え方やビジネスシーンでの活用方法についてわかりやすく解説いたします。

ロジスティック回帰分析とは？

ロジスティック回帰分析とは、特定の事象に対して発生するか否か、すなわち「0」か「1」かを予測する「2値分類」の分析手法です。
発展的なものとして、「2値」以上の分類である「多項ロジスティック回帰分析」や、序列のある分類である「序数ロジスティック回帰分析」も行うことが可能ですが、本記事では解説を省略いたします。

ロジスティック回帰分析は、2値分類の予測をする手法ですが、考え方や必要なデータなどは連続値を予測する重回帰分析と似ています。数学的な理論が似ていることから、使用できるデータも同じという特徴があります。分析に使用されるデータについては後述いたします。
ロジスティック回帰分析と重回帰分析の異なる点は、ロジスティック回帰分析の目的変数が質的な数字であるのに対して、重回帰分析の目的変数は量的な数字であることです。

ロジスティック回帰分析を使用するメリットは、判断の柔軟さと分析結果の解釈性があります。詳しくは次章にて解説いたします。

分析によってわかること

メリット①：判断の柔軟さ

ロジスティック回帰分析を用いることで、目的の事象どちらかが発生するか予測できることに加え、目的の事象が発生する確率を求めることもできます。
また、発生確率を求めることができるので「何%以上で目的の事象が発生したとみなす」というラインを自分たちで引くことができます。このことによって、「余程確信がない限り事象が発生するとは判別しない（90％以上）」や「少しでも可能性があるなら事象が発生すると判別する（15％以上）」など、ビジネスの要件やドメインに応じた運用をすることが可能です。

メリット②：結果の解釈性

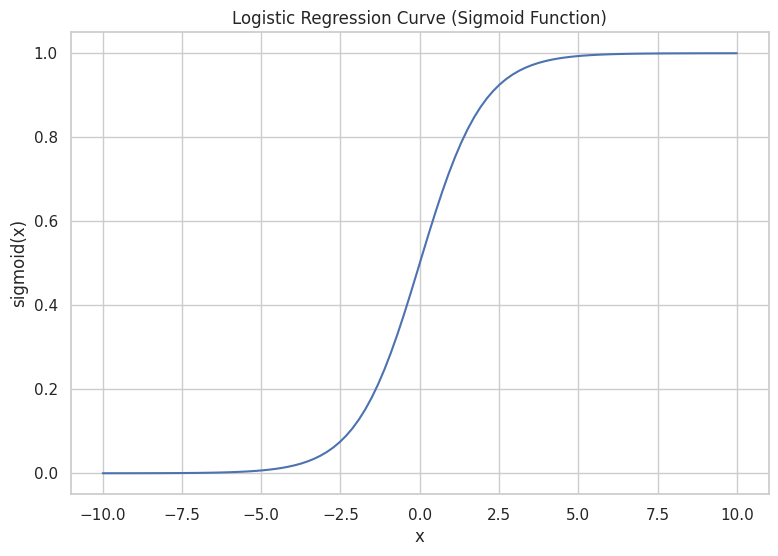
上記のグラフが表す関数はシグモイド関数と呼ばれ、以下の式で表すことができます。

$$y = \frac{1}{1 + e^{-z}}$$

そして、\( z \)には、以下の数式が入ります。

$$z = b_1X_1+b_2X_2+b_3X_3+…+b_0$$

上記の\( z \)に関する式は連続値を予測できる「重回帰式」と同じ形をしており、説明変数が線形結合されています。

つまり、ロジスティック回帰分析とは上記式において偏回帰係数にあたる\(b_n\)を求めることをいいます。
式の解釈としては、\(z\)が大きくなる（＋∞の方向に進む）とシグモイド関数の値は「1」に近づき、一方で\(z\)の値が小さくなる（－∞の方向に進む）とシグモイド関数の値は「0」に近づきます。つまり、\(b_n\)の値からどの変数が、目的の事象が「発生する」ことに寄与していて、どの変数が目的の事象が「発生しない」ことに寄与しているかを数値で算出することができるといえます。

ロジスティック回帰分析は「オッズ比」を用いて、「何倍発生確率が上昇するか」を知ることができます。「オッズ比」とは以下の式で表されます。

$$オッズ比=e^{b_n}$$

上記のようにオッズ比は、自然対数の\( e \)に偏回帰係数を指数として値を取ることで、表されます。説明変数の\( X_n \)が1増えることで、オッズ比の値だけ発生確率が倍になります。
具体的には、偏回帰係数が「0.8」だった時、オッズ比は「\( e^{0.8} \)」で表すことができ、その値は「約2.2255」です。つまり偏回帰係数が0.8である説明変数が1上昇すると、発生確率は約2.2255倍上がるということになります。このようにして結果を解釈します。

必要なデータ

続いては、ロジスティック回帰分析をおこなう際に必要なデータについて解説いたします。

予測の目的となる変数（目的変数）は、すでに述べた通り、二値の値を取るものとなります。

一方、説明変数は、何かの分類もしくはランク付けされた情報を表す変数（例：性別を0/1で表したもの、満足度を1/2/3/4/5の5段階で表したものなどです。これらは質的変数とも呼ばれます）を扱うことができます。いずれの場合も、数値であることが必要不可欠です。

具体的な例としては、会員顧客が自社のオンラインストアで販促キャンペーンをおこなった商品を購入するか否かを予測するために、直近の購買からの経過日数（連続値）やオンラインストアのアクセス頻度（連続値）や月間の購入金額（連続値）、キャンペーンの広告接触の有無などを使用することができます。

このように、オンラインストアでの購入有無を予測することに「寄与しそうな数値」を説明変数の候補として扱うことが重要であり、より効果的な予測をおこなう上で欠かすことのできない要素になります。一方で注意しなければならない点もあります。こちらについては、本記事の後半で解説いたします。

ロジスティック回帰分析のビジネス活用

続いては、ビジネスシーンでの具体的な活用方法について紹介いたします。

デジタル広告のクリック推定

デジタル広告は、コンバージョンもしくはクリックなどがKPIになることが多いかと思います。今回はその例として、デジタル広告のクリックをロジスティック回帰分析から推定する流れを紹介します。

目的変数を「そのセッションでクリックされたかされていないか」のフラグデータとし、説明変数をそのアクセスの情報（日時やどんなページを見たか（ページのカテゴリー情報）、滞在時間）、会員情報があれば会員情報に紐づくデモグラフィック情報、これまでのアクセス情報などを使用します。

アクセス日時	クリック	ページカテゴリ	会員フラグ	リファラ	…
2022/01/01	0	sports	1	search	…
2022/01/01	1	business	1	サイト内	…
2022/01/02	0	entertainment	0	search	…
2022/01/03	0	sports	1	search	…

また、デジタル広告のクリックは、一般的に偏りの大きいデータです。具体的にはクリックが発生しないアクセスが99％以上で、クリックが発生するアクセスが1％以下など不均衡の大きいデータであることがほとんどです。不均衡なデータに対する対応（アンダーサンプリングなど）が必要となりますが、本記事での紹介は割愛いたします。

さて、これらのデータを用いて、ロジスティック回帰モデルでクリック確率の推定をおこないます。推定結果が以下のようになったとします。

アクセス日時	クリック	ページカテゴリ	会員フラグ	リファラ	…	クリック確率
2022/01/01	?	sports	1	search	…	0.1
2022/01/01	?	business	0	search	…	0.15
2022/01/02	?	business	1	サイト内	…	0.9
2022/01/03	?	sports	1	search	…	0.2
2022/01/03	?	business	0	search	…	0.3
2022/01/04	?	entertainment	1	サイト内	…	0.6

この場合、クリックの有無を判別する閾値をクリック確率0.5以上とした場合、クリック確率が「0.6」「0.9」のアクセスがクリックされると判別されます。
クリックの確率が一定以上のページ訪問者にデジタル広告を当てることで、クリックが発生する確率が高まった状態での効率的な広告配信をおこなうことができます。

この「クリック確率0.5以上」という閾値は、分析者によって自由に変えることができます。
「デジタル広告はクリックされる割合がそもそも低いから、閾値ももっとさげるべきだ」という仮説に対応して、閾値を「クリック確率0.2以上」に変更したとします。すると、クリック確率が「0.2」「0.3」「0.6」「0.9」のアクセスがクリックされると判別される結果になります。

このようにロジスティック回帰分析は、判別の閾値を柔軟に変更することができるのも特徴のひとつです。加えて、仮説などに応じて閾値を変更するだけでなく、ROC曲線やAUCなどを用いて閾値を調整することも重要になります。

その他の活用事例

クリック予測のほかに、以下のような活用事例があります。

生産ラインでの異常検知

ロジスティック回帰分析は異常検知に用いることも可能です。クリック予測と同様に、不均衡なデータであることに注意が必要です。
これまでの生産ラインで故障や破損、不良品などの異常が発生しているかどうかを目的変数とし、説明変数に経過年数や総生産数、気温やメンテナンス頻度などを設定することで予測することができます。

これらの異常検知は、生産ラインに限らず、クレジットカードの不正利用やデフォルトの発生（債務不履行）、ネットワークやサーバーなどへの不正アクセスなどを予測することもできます。

ECサイトでの購買予測

ECサイトの購買予測にもロジスティック回帰を活用することができます。ただし、会員ログイン情報などによってサイトへのアクセスを識別する必要があることに注意が必要です。
購買に至るがどうかを目的変数として、ユーザーのサイト内行動履歴やサイトへの流入経路などを説明変数として予測することができます。クリック推定（上記の例を参照）を購買の有無として考えることで、より具体的に想像できるかと思います。

購買の予測に限らず、会員登録や来店予約などサイト上のコンバージョンを目的変数とすることでより幅広く活用することができます。

サブスクリプション契約の継続（解約）予測

ロジスティック回帰分析の「01判別」を用いることで、サブスクリプション契約の解約か継続を判別することができます。
目的変数を解約(0)と継続(1)とし、説明変数に利用頻度や契約情報、契約の長さなどを用いることで予測することができます。

ロジスティック回帰分析に限らず、決定木分析を用いることでも解約予測をおこなうこともできます。

あわせて読みたい

決定木分析（デシジョンツリー）とは？ビジネス活用や注意点を解説 「決定木分析（デシジョンツリー）」とは、使用できるデータの柔軟性や結果の見やすさから、多くのビジネスシーンで活用されてきた分析手法のひとつです。 本記事では、...

ロジスティック回帰分析の注意点

最後にロジスティック回帰分析をおこなう際の注意点について紹介いたします。

予測できるのは「0」か「1」

ロジスティック回帰分析は、「0」か「1」を判別する2値分類を目的とする分析手法です。そのため、重回帰分析のような「金額」や「人数」といった連続した数値を予測することはできません。ご注意ください。ただし、「0」か「1」のラベルへの所属確率を求めることはできます。

多重共線性に要注意

多重共線性とは、重回帰分析と同様にロジスティック回帰分析においても、最も注意すべき問題です。多重共線性が発生している予測式では、説明変数の標準誤差が大きくなり評価がうまくおこなえないことがあります。そのため、多重共線性はロジスティック回帰分析において、必ず避けるべき問題なのです。

では、多重共線性はどのような状況で発生するのでしょうか。その答えは高い相関関係にある変数同士が、説明変数として使われている場合です。

例えば、オンライン購買の有無を予測する際に、「月間のアクセス頻度」と「月間のアクセス回数」を説明変数に加えたとします。この時、多くの場合で多重共線性が発生します。なぜなら、アクセス頻度＝アクセス回数÷月間日数となり、アクセス回数が増えればアクセス頻度もそれに伴って増える関係性にあるからです。

上記の例のように変数の意味から明らかに相関関係がある変数同士の場合もあれば、実際にデータを見ないと明らかにできない場合もあります。変数が多くお互いの関係が見えにくい場合などは各変数同士の相関係数を総当たりで算出する「相関行列」を求めたり、その可視化などをおこなうと良いでしょう。
さらに、見せかけの相関を作る「交絡因子」などが潜んでいる可能性もあります。この場合、業界のドメイン知識やこれまでのデータの取り扱いなどを踏まえて、慎重に判断する姿勢が重要です。

まとめ

今回はロジスティック回帰分析について解説いたしました。

ロジスティック回帰分析は、「0」か「1」の二つの数値どちらかを確率で表す2値分類の分析手法です。紹介したように「特定の事象が発生するか否か」という分かりやすい状況を予測することができることに加え、その判断基準を自分たちの仮説や経験を用いることができるので、ビジネスの現場でも大いに活用することができます。

ロジスティック回帰分析における注意点を踏まえた、一歩深い分析の役に立てれば幸いです。

研究記事も執筆しています

データアナリティクスラボ

Open Interpreterの動かし方 | データアナリティクスラボ Indexはじめに使用したのPCの環境環境構築事前準備Docker上で作った仮想環境を使う方法手順OpenAI APIの利用状況の確認方法OpenAI APIを使用する場合の注意点セットアップ...

データアナリティクスラボ

日本語LLMにおけるトークナイザーの重要性 | データアナリティクスラボ Indexはじめに日本語LLMについてJapanese StableLM AlphaELYZA-Japanese-Llama-2-7bモデル評価本記事で取り上げるポイントトークナイゼーションとはトークナイゼーションの...

データアナリティクスラボ

イジングマシンで解く最適化問題の定式化 | データアナリティクスラボ Index1. はじめに2. イジングマシンとは3. イジングマシンのための定式化3.1. イジングモデルイジングモデルにおける定式化3.2. QUBO形式3.3. 定式化の違い数学的等価性人...