お気軽にお問い合わせください
主成分分析とは?手法の概要とビジネス活用事例を解説します!

「主成分分析(PCA:Principal Component Analyis)」とは統計解析手法の一つで、変数を要約して合成することで、変数の数を減らす「次元削減」手法のひとつです。
本記事では、「主成分分析」における考え方やビジネスシーンでの活用方法を解説いたします。
主成分分析とは?
「主成分分析」とは、大量にある系列データを要約して、少ない系列数のデータに減らす「次元圧縮」という統計解析手法です。特に、2次元・3次元に要約することができれば、データの特徴を可視化することができます。
主成分分析の手順を簡単に説明すると以下のようになります。

上記のデータで分散が最大となる方向に赤い直線を描きました。X軸方向の広がりを持つデータであることがわかります。
この赤い直線が『第1主成分』となります。
次に赤い直線に対して、『直交』する方向で、分散が最大となる向きを見つけます。その結果が以下のグラフです。
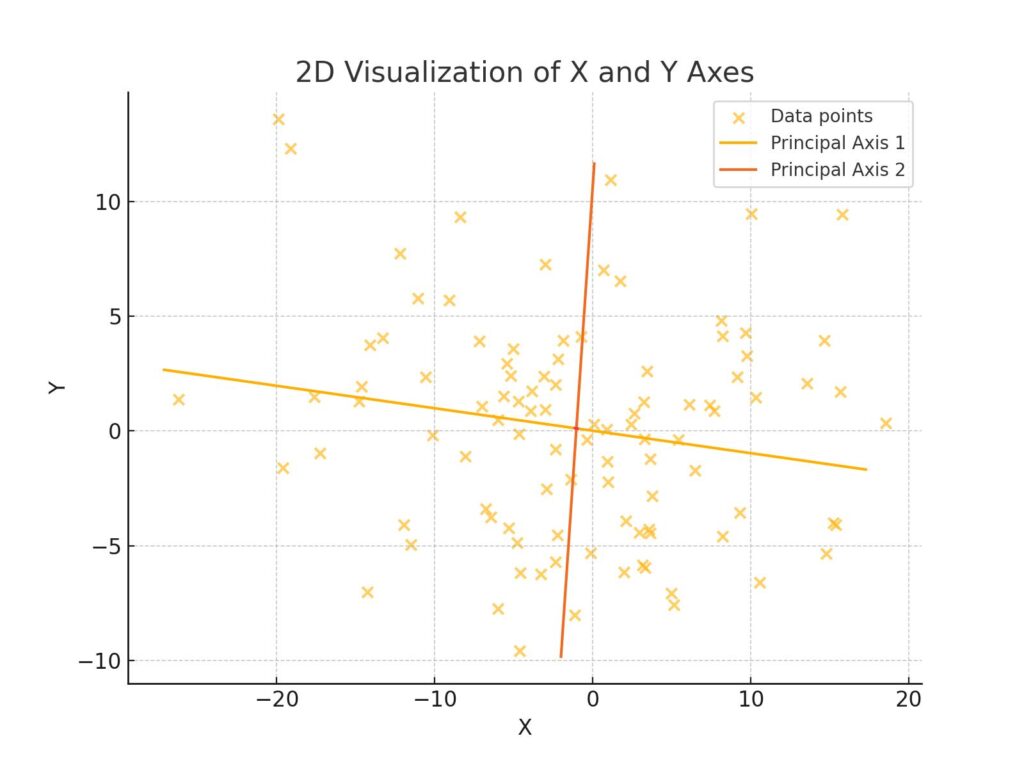
Y軸に伸びたオレンジ色の直線を描くことができました。このオレンジ色の直線が『第2主成分』となります。
このプロットは、背後にZ軸方向にもデータを持つため、XY軸の2次元上では見かけ上直角には交わってはいません。しかし、Z軸の計算を踏まえると、相関関係のない『直交』の関係となっています。
次に第3主成分となる方向にも求めると、以下のようなグラフになります。
最後に、これらの軸の意味を解釈します。軸を解釈するとは、軸を表現している主成分負荷量などから判断します。『〇〇の要素が多く含まれているから、△△的な意味合いを持つ軸だ』というような解釈をする必要があります。これには、深いドメイン知識や経験を要することがあります。
一方で、『次元圧縮』や『変数削減』のみを目的とした場合の主成分分析では、軸を解釈する必要がないこともあります。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。主成分分析による分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
分析によってできること
「主成分分析」をおこなうことで情報を要約することができます。情報が要約されることで、より低次元な空間で可視化することができます。
ただし、これらの要約情報は数学的に求められるものであり、ビジネス上の意味を持つ情報の圧縮がおこなわれるとは限りません。そのため、分析結果の解釈には専門家の知見やドメイン知識の活用が重要となります。
主成分分析においては、「主成分負荷量」や「累積寄与率」などを算出することで要約された情報の有効性を判断することができます。主成分分析をおこなうために以下の数値などを算出します。
| 用語 | 意味 | 用途 |
| 固有値 | データの分散が各主成分にどれだけ説明されているかを示す値。 | 固有値が大きい主成分ほどデータの特徴を多く説明しているため、主成分の選択に使用される。 |
| 寄与率 | 各主成分が全体のデータの分散に占める割合を示す値。 | 主成分分析全体で重要な主成分を選ぶ際に使用される。 |
| 主成分負荷量 | 元の変数が主成分にどれだけ寄与しているかを示す値。 | 寄与している変数から主成分の解釈に使用される。 |
| 主成分得点 | 各データ点が主成分空間上でどの位置にあるかを示す値。 | 主成分空間でのデータの分布を可視化し、クラスタリングや異常値検出などに使用される。 |
また、主成分分析を次元削減の手法として活用することで、クラスター分析や重回帰分析で扱う変数を減らすための手法として使用することができます。
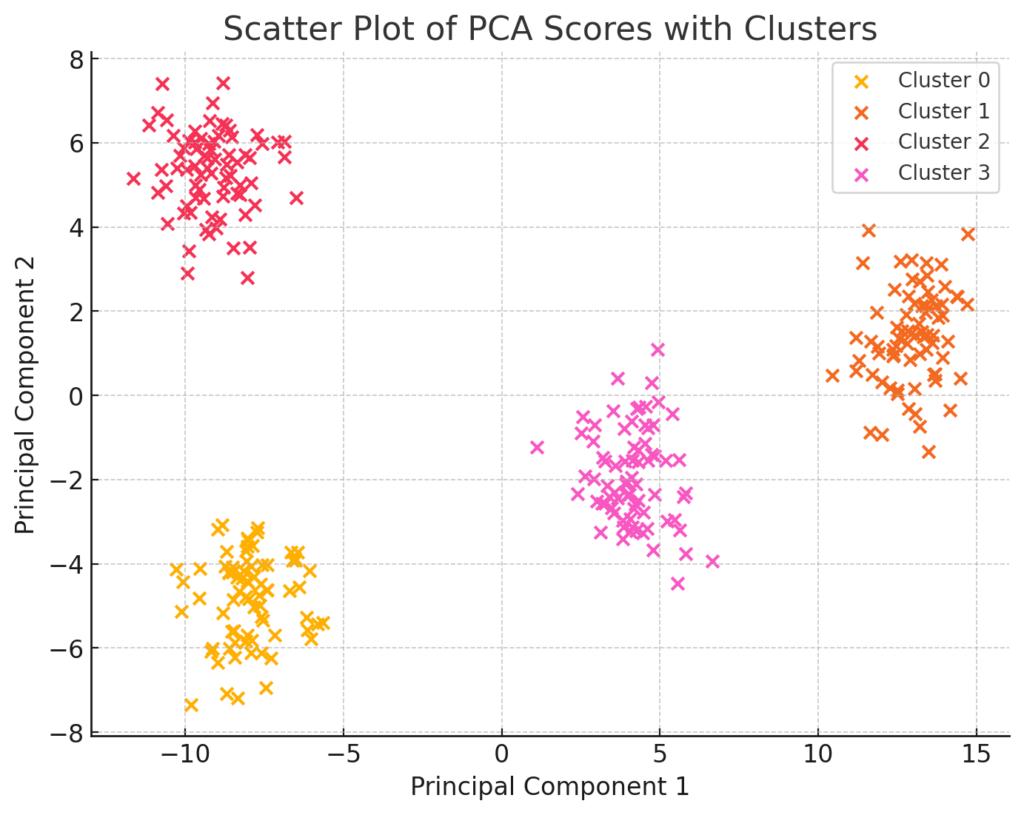
このようにして、主成分分析を使いこなすことができれば、ビジネスでも強力な武器となります。
必要なデータ
「主成分分析」が対象とする主たるデータは量的データとなります。ただし、多変量の量的データにおいては、変数間において数字のスケール(単位など)が合わないことがあります。
例えば「金額」や「距離」、「時間」、「人数」など様々な尺度の変数を組み合わせて使用したい場合があるかと思います。このような場合、データを「標準化」すると分析しやすくなります。
ただし、「主成分分析」で検索した際に出てくる複数科目のテストの成績を主成分分析するような場合は、変数間のスケールが一致していると考えられるため、そのまま主成分分析を適用することができます。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。主成分分析による分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
ビジネスシーンでの活用
次にビジネスシーンにおける主成分分析の具体的な活用方法についてご紹介いたします。
アンケートデータに対する主成分分析
会員に対してアンケートを取り、新形態となった店舗の再利用意向を調査する場合を解説いたします。
200名から回答を得ることができ、以下のような結果となりました。
| 回答者 | サービスの満足度 | 商品の品揃え | 立地 | 店員の対応 | 清潔感 | 再利用意向 |
|---|---|---|---|---|---|---|
| 1 | 5 | 4 | 5 | 5 | 5 | なし |
| 2 | 1 | 4 | 4 | 4 | 4 | なし |
| 3 | 3 | 3 | 3 | 3 | 3 | あり |
| 4 | 5 | 5 | 4 | 4 | 5 | なし |
| 5 | 4 | 1 | 4 | 1 | 4 | なし |
| … | … | … | … | … | … | … |
| 200 | 5 | 5 | 4 | 5 | 5 | あり |
このアンケート結果を用いて主成分分析をおこないます。その結果、以下のような分析結果を得たとします。
| 第1主成分 | 第2主成分 | … | |
|---|---|---|---|
| 寄与率 | 0.477939 | 0.181535 | … |
| 累積寄与率 | 0.477939 | 0.659474 | … |
累積寄与率を見ると、2つの主成分でおよそ65%説明できることがわかります。
今回のアンケートデータでは、質問が少ないためこのような数値が得られることは十分に考えられます。しかし、より現場の視点に立った時、これよりもさらに多い20個以上などの質問に対して、主成分が二つのみで6割以上の説明が出来ているのであれば、かなり情報を圧縮できているといえるでしょう。
次に、主成分負荷量を確認します。
| サービス満足度 | 品揃え | 立地 | 店員の対応 | 清潔感 | |
|---|---|---|---|---|---|
| 第1主成分 | 0.548997 | 0.338857 | 0.490721 | 0.584875 | -0.029879 |
| 第2主成分 | 0.061514 | 0.003355 | 0.731253 | -0.676421 | -0.062672 |
以上の結果から、第1主成分に関しては、清潔感を除くアンケートの各質問が高得点であるほど再利用意向が高いことがわかりました。清潔感については、値が0に近いことから、第1主成分に与える影響は小さいことがわかります。
第2主成分に関しては、「立地」に関する回答が大きく影響していることがわかります。
これらの結果をもとに主成分得点を算出し、第1主成分(PC1/x軸)、第2主成分(PC2/y軸)を散布図にすると以下のようになります。
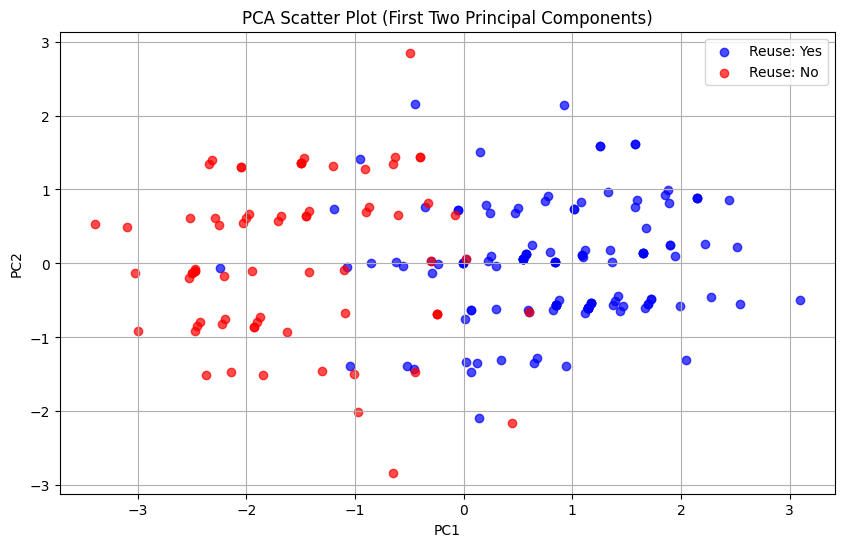
この結果から、傾向として第1主成分(PC1:X軸方向)が高いほど再利用意向があることがわかります。一方で、第2主成分(PC2:Y軸方向)は、再利用意向の有無に関わらず、プロットが散らばっていることから再利用意向への影響はあまりないと考えられます。
各成分の主成分負荷量と合わせて解釈すると、次のような解釈をすることができます。
第1主成分のスコアは「店員の対応」「サービス満足度」の影響を受けているので、これらをまとめて「総合的な接客」と解釈し、これらのニーズを満たすことが再利用へとつながりやすいことが考えられます。
一方でこの数値が低いことで再利用意向をなくしてしまうことから、この点において店員の教育を重視する必要があると考えることもできます。
第2主成分として立地の回答は、再利用意向に関わらずまばらであるため、再利用意向には大きく影響していないことがわかります。このことから、ある程度立地条件が悪くても、「総合的な接客」で再利用顧客を囲い込める可能性があることが考えられます。
このようにして、アンケートデータに主成分分析を用いて情報の要約に活用することができます。
今回の例のように、きれいに主成分の解釈をすることが出来ても、「アンケートに回答してくれる人はそもそも再利用の傾向がある」ということも考えられます。仮説を証明することは有効であっても、ここからの施策にはつながりにくいかもしれないことに注意する必要があります。
また、今回のようにきれいに解釈が出来ないような結果になってしまうこともありえます。主成分分析以外にもクロス集計などの基礎的な分析も掛け合わせながらおこなうことで、より緻密な分析とすることができます。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。主成分分析による分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
そのほかのビジネス活用事例
- ブランドのポジショニング分析
-
自社のブランドイメージと競合他社との差別化を図るべく、飲料会社がユーザーへのアンケートを実施しました。
その結果に対して主成分分析を実施し、多くの質問項目から『健康志向』や『高級志向』と解釈できる2軸を算出。競合他社とのポジショニングの違いや、空白領域となっているブランドイメージへの戦略検討に活用した事例などがあります。ポジショニング分析の類似した手法としては、以下の『コレスポンデンス分析』もございます。
Data Analytics Magazine コレスポンデンス分析とは?ビジネス活用や注意点を解説! | Data Analytics Magazine コレスポンデンス分析(Correspondence Analysis)とは、アンケートなどにおいて概要を分析するための手法です。本記事では、コレスポンデンス分析の方法やビジネス活用例…
コレスポンデンス分析とは?ビジネス活用や注意点を解説! | Data Analytics Magazine コレスポンデンス分析(Correspondence Analysis)とは、アンケートなどにおいて概要を分析するための手法です。本記事では、コレスポンデンス分析の方法やビジネス活用例… - 主成分回帰分析への活用
-
主成分回帰分析とは、主成分分析を実施して削減した変数を用いて回帰分析をおこなう手法のことをいいます。この手法のメリットは、変数間での多重共線性を回避できることがあります。
このメリットを活用して、重回帰分析による売上予測を実施している事例などがあります。
Data Analytics Magazine 重回帰分析とは?数値予測の第1歩! | Data Analytics Magazine 重回帰分析は、売上予測や新規会員数予測などビジネスシーンで多く活用される分析手法の一つです。重回帰分析の考え方や活用方法について解説します。
重回帰分析とは?数値予測の第1歩! | Data Analytics Magazine 重回帰分析は、売上予測や新規会員数予測などビジネスシーンで多く活用される分析手法の一つです。重回帰分析の考え方や活用方法について解説します。
注意点
次に、主成分分析の注意点を3つ紹介します。
情報は削減されてしまう
「主成分分析」は情報を圧縮する手法です。当然ながら情報の総量は減ります。それを理解した上で主成分分析をおこなうことが重要です。
情報が損なわれる以上に、情報を要約・圧縮して可視化できたり解釈を得るなどのメリットが大きいのであれば、主成分分析は力強い武器になります。
主成分分析と併せてほかの分析も並行しておこない、扱うデータがどのような形で要約・圧縮されるかの結果を確認することも重要です。
本記事では主成分分析(PCA)を対象としていますが、他にもNMF(Non-negative Matrix Factorization:非負値行列因子分解)、2種類のLDA(Latent Dirichlet Allocation:潜在的ディリクレ配分法/Linear Discriminant Analysis:線形判別分析 ※LDAは異なる2種類の次元圧縮手法が同じ略称を使うため注意が必要)、t-SNE(t-Distributed Stochastic Neighbor Embedding:t分布型確率的近傍埋め込み法)など目的や特性に応じた次元圧縮手法を複合的に試しながらビジネスニーズに即したものを探索する姿勢も重要です。
主成分の解釈は主観に基づく
主成分分析をおこなうことで、変数が要約・圧縮されます。つまり複数の変数同士が「似た者同士」としてまとめられます。「主成分の解釈は主観に基づく」とは、「第1主成分は〇〇と××の要素が入っているから、△△とまとめられる」という意味になります。
このような形できれいに要約できて言い換えまでできることは稀で、実務上ではなかなかうまく解釈できないということがよく起こります。その際はひとまとまりのデータを性別や年齢、または時間や場所など様々な切り口で切り分けてから、再度主成分分析を実行することで、有意義な結果が得られることがあります。
上記のことから、先述の通り主成分分析では高いレベルでの分析結果の解釈や、深いドメイン知識の活用が重要となります。
因子分析との違い

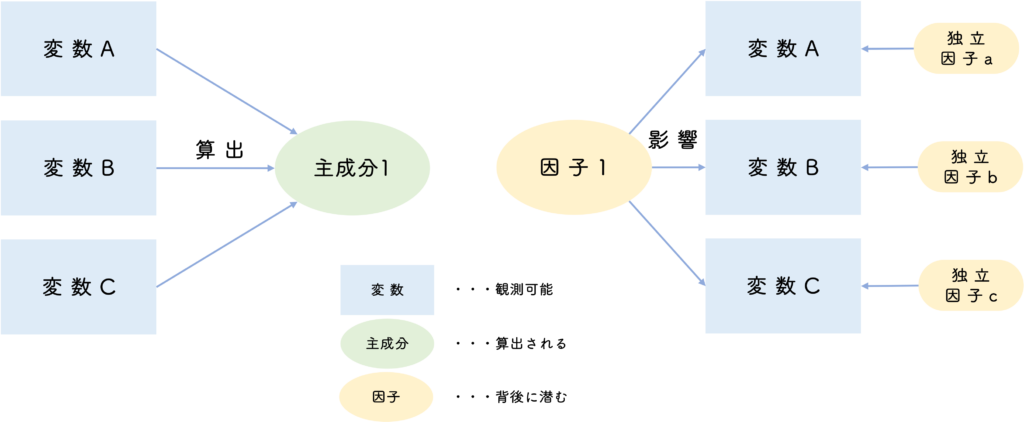
主成分分析と因子分析は、多変量のデータと少数の因子・主成分の関係性を探る分析という点で類似しています。これらの分析手法の決定的な違いは、原因と結果の矢印の関係性です。
主成分分析は、今手元にある変数(データ)を使用して新たな変数(データ)を作る手法です。一方、因子分析は今手元にある変数(データ)の共通因子を探る手法となります。
まとめ
主成分分析は、なるべく情報を落とさないように多くのデータを要約する次元削減の統計的分析手法です。データを要約・圧縮することで、可視化などを容易におこなえるようになります。このことから、ビジネス上で活用することができれば強力な武器となりえます。
しかし、計算が複雑だったり得られた結果の解釈が難しい場合もございます。また、「情報が削減されてしまうこと」、「主成分の解釈は主観」などに注意が必要です。これらの注意点を理解した上で主成分分析を活用することが重要です。
主成分分析の特性や注意点を踏まえた、一歩深い分析の役に立てれば幸いです。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。主成分分析による分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
こちらもご覧ください



















