お気軽にお問い合わせください
因果フォレストとは?概要とビジネス活用例を徹底解説!

近年、個々の属性に応じた施策の効果を正確に推定する因果推論に注目が集まっています。
特に因果フォレスト(Causal Forest)は、個人の性別・年齢・収入などの属性に基づいた異なる効果(異質性)を分析する手法のため、「誰に」「どのくらい」施策が効果的かを明確に示すことができることから、マーケティング分野などの意思決定において活用されています。さらには臨床試験、公共政策、経済学など、多岐にわたる分野での施策決定に非常に有効な手段となるため注目を集めています。
因果フォレストの前提
因果推論における因果効果の推定では、一般的に個人ごとに対して施策の効果を推定するのではなく、施策実施グループと施策非実施グループに対して目的変数(結果として見たい指標)の平均を求め、その差分を因果効果とする平均介入効果(ATE:AverageTreatment Effect)を求める手法が用いられます。
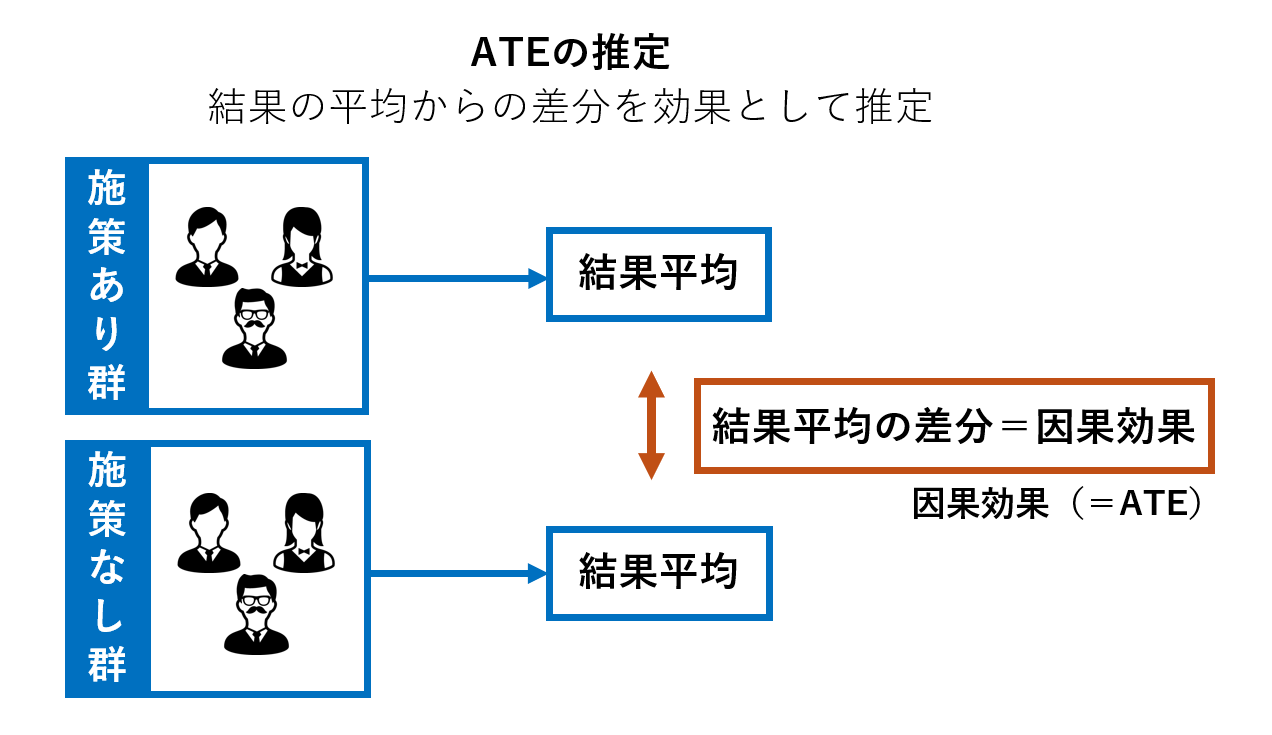
しかしながらATEでは、個人や属性ごとに異なる効果がある場合その測定ができません。
そこで今回は個人や属性ごとに異なる効果である「異質性」を推定する手法として因果フォレストについて紹介します。
- 因果推論
-
原因と結果の関係性について、影響の有無や大きさを推定、分析すること
- 因果効果の推定
-
施策やキャンペーンなどを実施した際、結果となる指標(売上、CV率など)に対して効果があるのか、またどのくらいの大きさかを測る指標
- ATE(Average Treatment Effect:平均介入効果)
-
施策実施したグループ(介入群)と施策実施していないグループ(対照群)それぞれの結果の平均を算出し、その差分を因果効果として推定する手法
- 異質性
-
個人や属性ごとに異なる介入効果があることを指す
この異質性を推定できる効果を条件付き平均処置効果(CATE:Conditional Average Treatment Effect)や個体別処置効果(ITE:Individual Treatment Effect)という
因果フォレストとは
因果フォレストとは異質性による因果効果を推定できる手法になります。この手法を使用することで施策が「誰に」「どのくらい」効果があるのかを見ることができます。
例えば、若年層の男性向けにキャンペーンを実施した場合以下のように20代男性には4,000円の売上増加、20代女性には4,000円の売上減少、50代の男女では売上に因果効果がなかった事例を考えます。
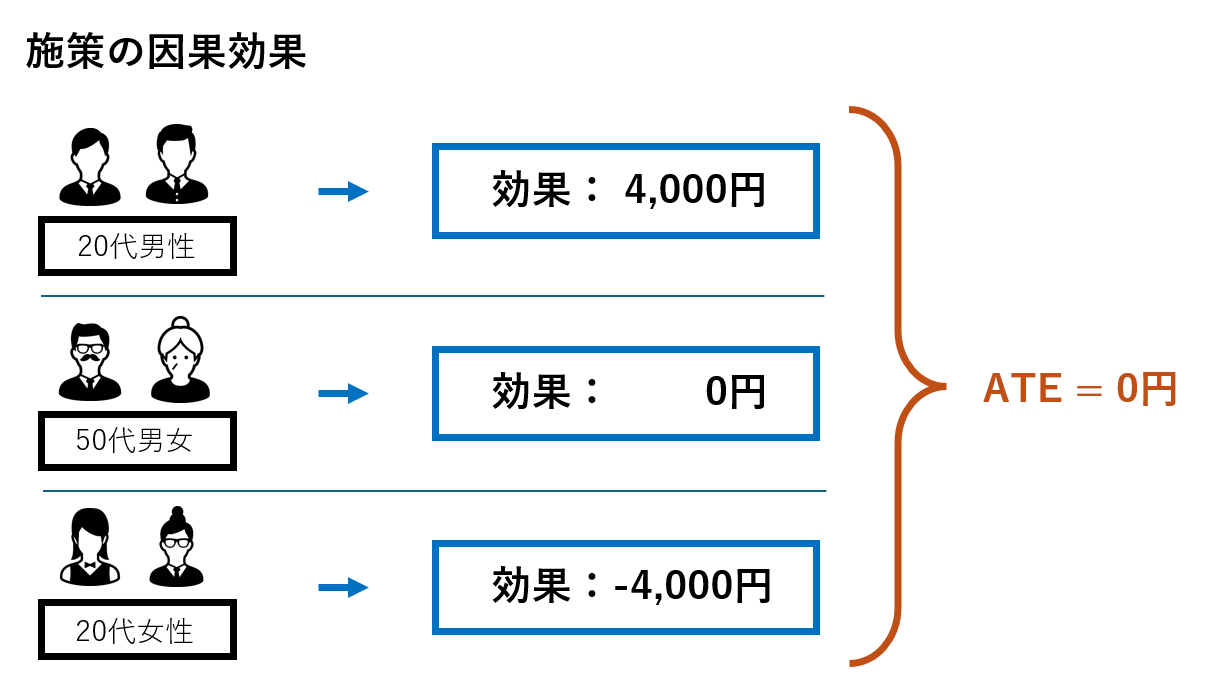
ATEで見ると0円と因果効果がないという結果になりますが、異質性を考慮すると20代男性に因果効果があることが考えられます。この例を因果フォレストの結果として出力すると以下のようになります。
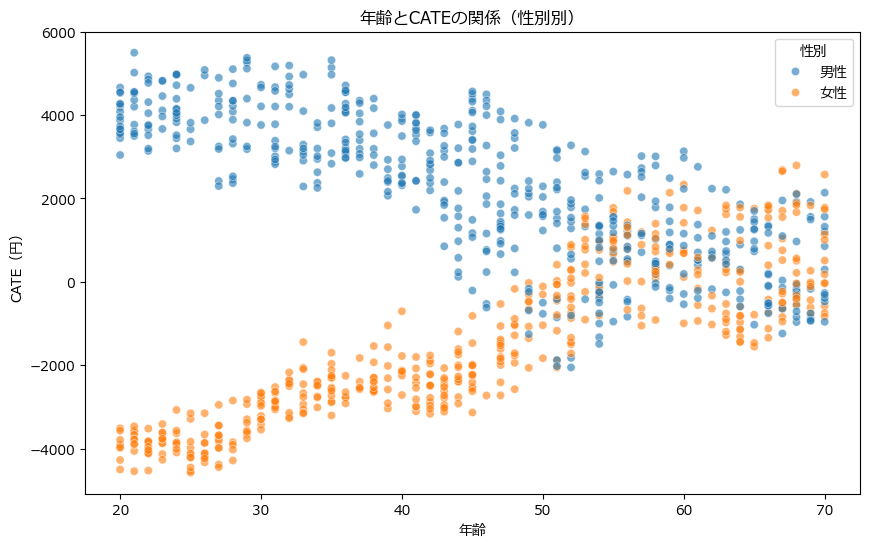
Y軸に因果効果(今回は円)で、X軸に年齢、男性女性で色分けして表現しています。
上図からも、男性は20~40代で年齢の正の因果効果が考えられ、女性は20~40代で年齢の負の因果効果があると考えられます。一方、男女共に50代以降は年齢の因果効果がないと考えられます。
このように因果フォレストを用いることで「誰に」「どのくらい」効果があるのかを推定することができます。これにより男性の20~40代にターゲットを絞りキャンペーンを実施することで、全員を対象に実施するよりコストが低く、かつ高い効果を期待することができます。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。因果フォレストによる分析の実績なども多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
ビジネス活用例
先述の通り、因果フォレストはマーケティング、CRM、臨床試験、公共政策など多岐にわたる効果測定で使用できるものです。以下の場面でも有効とされています。
- ランダム化実験が困難である場面
- 非線形性や異質性の因果効果の推定する場面
- 予測モデルの構築と因果効果の推定の両方が重要な場面
- 大規模なデータセットや高次元のデータを用いた因果効果の推定する場面
製薬会社での活用例
製薬会社の取り組みとして、「どのような属性を持つ人が目的変数に対してより効果的か」を分析するために、因果フォレストが使用された場合があります。具体的には、薬品の摂取を処置(介入)とした時に、身長や体重の大小、年齢や生活規則などどのような条件・属性が薬品の効果を高めるのかを明確にするという例です。
これにより、薬品を摂取することが有効か、有効な場合どのような人に対して有効なのかを明確にすることができます。
本記事では条件や属性による効果の違いである異質性を証明するために因果フォレストを用いた分析例について紹介します。
以下ようなデータを用いて分析した例を考えます。
- RCTされた処置群(薬品摂取グループ)と対照群(薬品非摂取グループ)データ
- ある指標の変化量(+2 ~ -2の間を推移し、+域であれば正の影響、-域であれば負の影響を示している)
- 属性データ(性別、年齢)、行動データ(薬品摂取方法、睡眠時間)等
上記のデータに対して因果フォレストを用いて以下の手順で実施します。
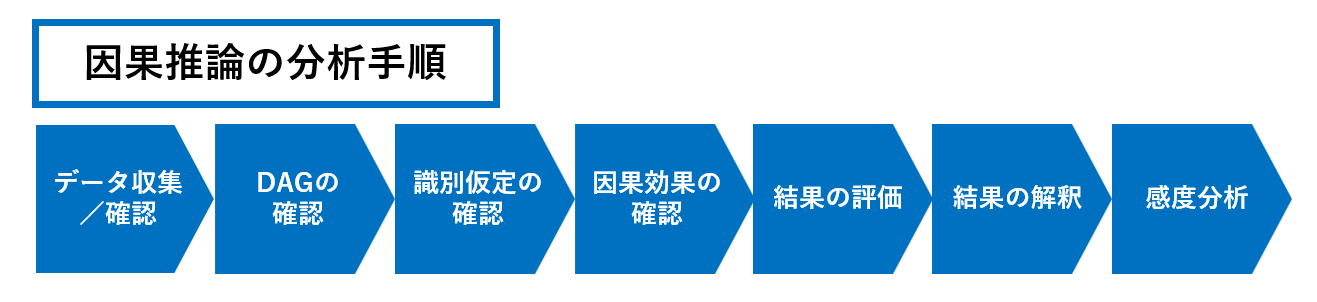
上記のフロー図は、因果推論をおこなう際の手順になっております。この手順で実施することで、実際の因果効果に対して過剰、過小に推定してしまうバイアスを除去しながら実施し、間違った結論になってしまうことを防ぎます。
データ収集・確認のフェーズでは、因果推論を実施する上で、因果効果を過大、過小に推定してしまうことを避けるために分析データの性質を理解することが目的です。
具体的には、時系列データの有無や欠損値の確認、SUTVAや正値性などを確認します。
データ収集後に情報バイアス(入力ミスなどによって発生するバイアス)や選択バイアス(収集データの偏りによって発生するバイアス)が生じていないか確認し、バイアスがある場合は適切な処理をおこなう必要があります。
これらを確認した上で、適切な処置や分析手法を選択すると、正しい因果効果の推定を得ることができます。
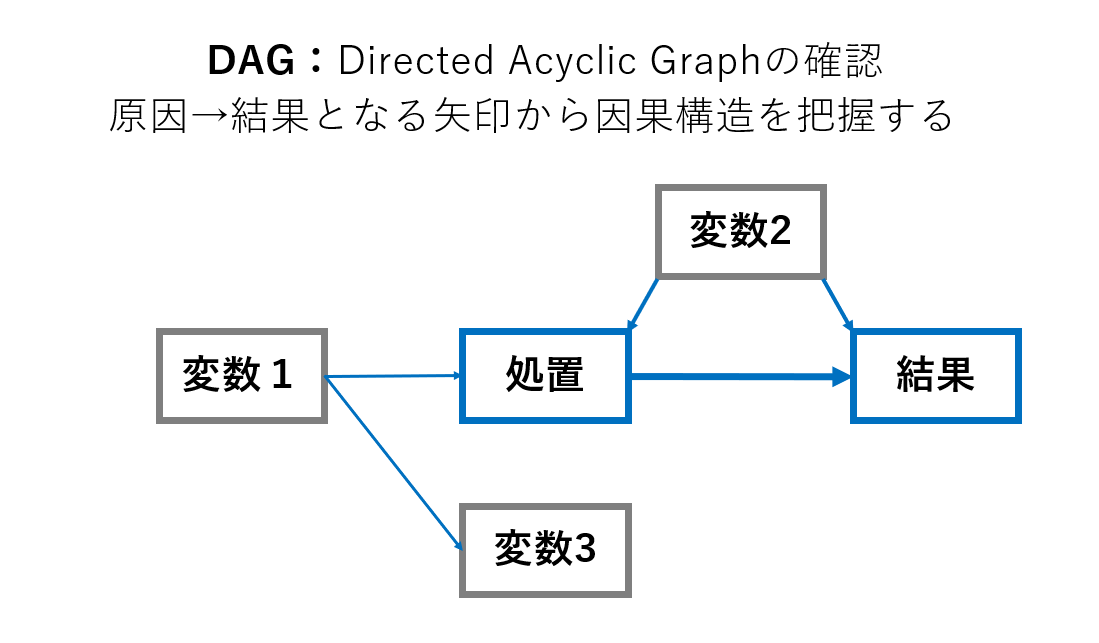
DAG(有向非巡回グラフ:Directed Acyclic Graph)とは、変数に対して原因と結果の間の矢印の向きを確認し、その因果構造を把握するためのグラフです。これにより、バイアスになり得る要因を把握することができます。またこの手順では、因果構造が自明か、自明ではないかによってアプローチが変わります。
- 因果構造が自明な場合
- バイアスになり得る構造になっていないかを確認する
- 因果構造が自明でない場合
- 因果構造、方向を仮説として設定し分析を進める
- 因果探索により因果の方向を推定する
因果効果を推定できるデータ足り得ているかどうかを識別仮定の確認を通して実施します。この仮定を満たしていない場合は結果の妥当性が弱くなってしまう点に注意が必要です。
識別仮定としては大きく2つあり、それは、①識別可能性と②SUTVAと呼ばれるものです。
- 識別可能性:観測データから母数が一意に推定できる状態
- SUTVA(stable unit value assumption):処置を受ける個体において処置の効果が安定している状態
上記を確認することで、因果推論をおこなう上で適切なデータかどうかを確認することができます。
因果効果の確認では、因果効果を推定するためのモデルを構築し、その結果をグラフで確認します。
これまでの過程(STEP)で、バイアスになり得る部分を調整したのち、モデルを構築します。Causal Forest DMLというライブラリを使用することで手軽に構築することができます。
Causal Forest DMLでは下記4点を設定した上で、パラメータを調整します。
| 変数 | 説明 | 本事例の場合 |
| 目的変数 | 因果関係の果の部分であり、施策実施の結果を示す変数 | ある指標の変化量 |
| 処置変数 | 施策を実施したかどうか(2値)や施策の段階(連続値など)を示す変数 | 薬品を摂取した処置群か薬品を摂取していない対照群を示す変数 |
| 説明変数 | 異質性を理解するために使用される変数 | 性別、年齢、行動データ(薬の摂取方法、睡眠時間) |
| 制御変数 | 目的変数と処置変数との関係でバイアスになり得る変数がある場合こちらに含めることで影響を制御することができる変数 | 対応なし |
上記をもとにモデルのパラメータを調整して因果効果を確認します。
説明変数に対してそれぞれ効果を算出し、グラフで出力します。グラフから読み取れることとドメイン知識をもとに、結果の整合性を評価します。
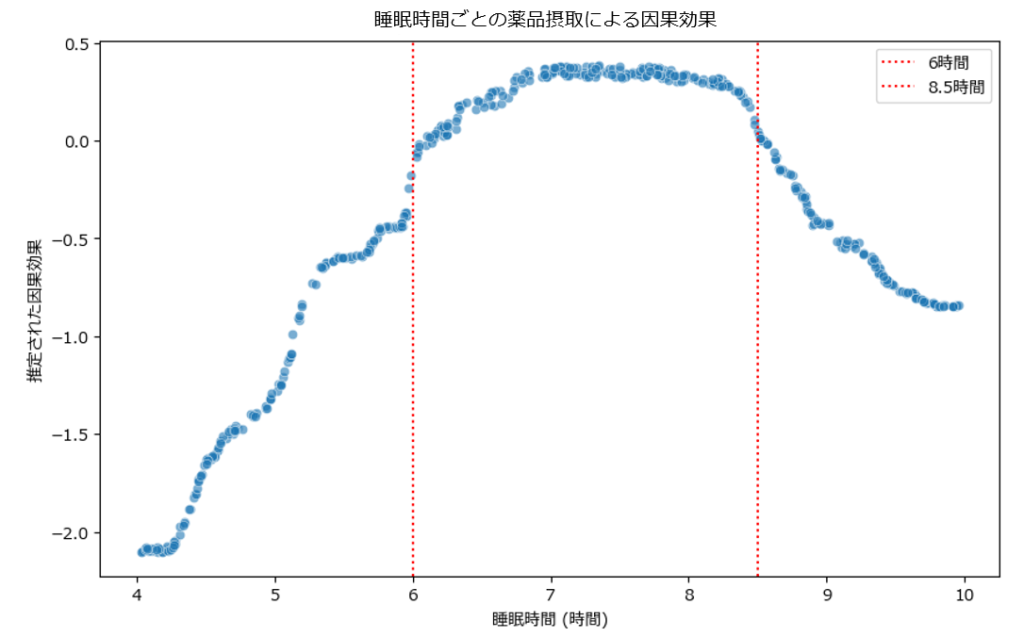
睡眠時間を説明変数に設定した場合、以下のような出力イメージになります。
結果の評価では結果の妥当性や統計的な評価、誤差の検証等をおこないます。
もっともらしい結果かどうか、以下のような方法を組み合わせて評価します。
- 可視化による評価
- 変数重要度による評価
- ドメイン知識やこれまでの経験による評価
- 標準化平均差(SMD:Standardized Mean Difference)による評価
- 推定値の標準誤差などから算出されるモデルの信頼性を用いた評価 など
変数重要度やドメイン知識を元に評価した結果、睡眠時間の違いで薬品の効能に影響があると推定できる、などと結果を評価します。
取捨選択した結果をもとに、算出されたグラフから解釈をつけていきます。

上記の結果は、睡眠時間が7時間~8時間の人に対して薬品の摂取によって正の変化があり、睡眠時間が6時間以下の人や睡眠時間が8.5時間以上の人に対して薬品の摂取によって負の変化があることが推測される結果となりました。
つまり、この薬品を摂取する際は、一般的に適切といわれる長さの睡眠を取ることが効果的で、そうでない睡眠時間の場合には負の影響を与える可能性がある、と解釈することができます。
感度分析とは、モデルのパラメータや変数の値を変化させたときに、その結果がどの程度変化するかを定量的に把握することを指します。
特に、未観測な交絡因子(遺伝による体質など、データの中にはなく取得しづらい変数などで処置変数や目的変数に影響を与えてしまう変数)が存在する可能性を考慮して、その影響やモデルの安定性を評価して感度分析を実施します。
以上の因果推論の手順に沿って分析を実施しました。
実施手順や考慮すべき変数などは複雑ですが、これらのステップを経ることで解釈しやすい結果を得ることができます。因果フォレストの強みは、まさに解釈しやすいことにあります。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。因果フォレストによる分析の実績なども多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
注意点
因果推論で正確な効果を推定するにあたって以下の点に注意が必要です。
- データセットに問題はないか?
-
データの欠損やバイアスを含んでしまっていないか確認する必要があります。
特に発生・混入しやすい、情報バイアス(入力ミスや測定方法によってばらつきが生じることで発生)や選択バイアス(収集したデータに偏りがある場合に発生)が含まれていると、誤った結果となってしまいます。 - 因果構造に問題はないか?
-
因果構造に問題がないかをチェックするために以下のような点に注意が必要です。
◆DAGで表現している場合、次の要素が明確になっているか
- 共変量:処置変数や結果変数に影響を与え、かつ処置変数の影響を受けていない変数のこと。
無視した場合、共変量の影響により因果効果を誤って推定してしまう可能性があります。 - 交絡因子:処置変数と結果変数の両方に影響を与える変数のこと。
調整しない場合、説明変数と結果変数の間に因果関係がないにもかかわらず、因果関係があるように見せてしまう。見かけ上の因果関係が生じる可能性があります。 - 中間変数:処置変数の影響を受けており、その変数が結果変数に影響を与えているの変数のこと。
誤った調整(モデルから除外など)をすると、因果経路が断たれ、処置変数の影響が過小評価される可能性があります。
Causal Forest DMLでは上記の変数を制御変数に含めることで調整可能です。
◆次の要素を識別できているか
- d分離:DAGにおける変数の独立性を判定するルールのこと。
d分離を利用して交絡因子を調整することで、スプリアスな因果関係や交絡バイアスを防ぐことが可能になります。 - バックドア基準:処置変数から結果変数へ向かう交絡経路を遮断するために、調整すべき変数を特定するルールのこと。
バックドア基準に基づいて適切な変数を調整することで、交絡因子による影響を除去し、因果推定の偏りを最小化することが可能になります。 - フロントドア基準:バックドア基準を利用できない場合(未観測の変数がある場合など)に中間変数を利用して因果効果を推定する方法のこと。
フロントドア基準は、中間変数を活用することで、交絡因子が直接制御できない状況でも因果効果を推定可能になります。
- 共変量:処置変数や結果変数に影響を与え、かつ処置変数の影響を受けていない変数のこと。
- 識別仮定を満たしているか?
-
識別仮定を満たしているか確認するために、識別可能性とSUTVAを確認する必要があります。
識別可能性を確認するためには①独立性②正値性が成立しているかどうかを確認する必要があり、SUTVAを確認するために③相互作用の有無④一致性を確認する必要があります。用語説明- 識別可能性:観測データから母数が一意に推定できる状態
-
①独立性(交換可能性)
施策を実施した場合、実施していない場合に関わらず、結果が独立している状態
②正値性
施策実施される確率、施策実施しない確率のどちらかに割り当てられる確率が0でない状態 - SUTVA:処置を受ける個体において処置の効果が安定している状態
-
③相互作用なし
潜在的結果変数が他の個体の処置状態に依存しない状態
④一致性
処置の結果が潜在的な結果と一致する状態
まとめ
因果フォレストでは異質性による因果効果を推定し、施策が「誰に」「どのくらい」効果があるのかを見ることができます。
この手法はマーケティング、臨床試験、公共政策、経済学など、多岐にわたる分野での施策決定に非常に有効であり、結果の解釈がわかりやすいため、データ分析について詳しくない方に対して強い説得力を与えるものとなります。
因果フォレストの特性や注意点を踏まえた、一歩深い分析の役に立てれば幸いです。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。因果フォレストによる分析の実績なども多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
こちらもご覧ください


















