お気軽にお問い合わせください
クラスター分析とは?わかりやすく解説!

データマイニング手法のひとつでもある「クラスター分析」は、ペルソナの分析や競合分析などマーケティングの分野などビジネスの現場で多く活用される分析手法の一つです。
本記事では、この「クラスター分析」について、考え方やビジネスシーンでの活用方法についてわかりやすく解説いたします。
クラスター分析とは
クラスター分析は、距離や類似度に基づいてデータをグルーピングする手法です。グルーピングの考え方として階層型と非階層型があります。階層型における代表的なグルーピング手法として「ウォード法」があり、非階層型における代表的なグルーピング手法として「K-means法」があります。
なお、グルーピング・分類の手法は「ハードクラスタリング」と「ソフトクラスタリング」のふたつに分類することもできます。「ハードクラスタリング」はすべての分類対象を、どれかひとつのクラスターに所属させる分類手法です。一方、「ソフトクラスタリング」はすべての分類対象が、それぞれのクラスターにどれくらいの確率で所属するかを表す分類手法です。
本記事では、「ハードクラスタリング」について解説いたします。
分析によってわかること
クラスター分析によってわかることは、分析対象(会員データや商品・サービス情報など)同士が「どれだけ似ているか」です。また、可視化をおこなうことで分析対象が「どれだけ似ていないか」を表すことにも適しています。
クラスター分析は、ビジネスで使われる様々な変数を組み合わせておこなうことで、グループ化された結果から知見を得るための手法とも言えます。
選択した変数や要素から、各グループがどのような意味合いを持つのか、などの業務上の仮説立てに活用することができます。例えば、どれくらいの頻度で自社サービスを利用しているか、などからグルーピングされたクラスターを優良顧客群や離脱予備群と考えたりすることができます。詳しくは「ビジネスシーンでの活用」にて解説いたします。
階層クラスタリング
階層クラスタリングとは、あらかじめ何個のクラスターに分類するか決める必要のない方法であり、データ数が少ない場合に適用しやすい手法です。以下のようなグラフを生成して分類をおこないます。
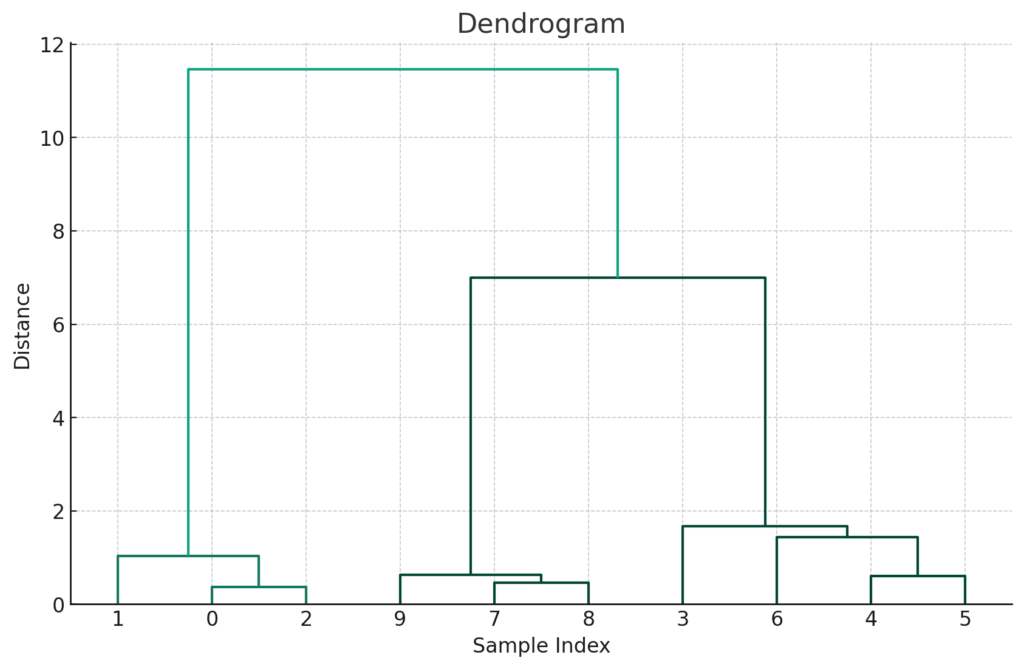
このような樹形図を「デンドログラム」という
上図の「トーナメント表」のようなグラフは、「デンドログラム(樹形図)」といい、階層クラスターを表しています。任意の高さで横に切り分けることで、クラスターに分けることができます。「どの高さ」で「何個に」分けるかは、人が判断する必要があります。具体的には以下のようになります。
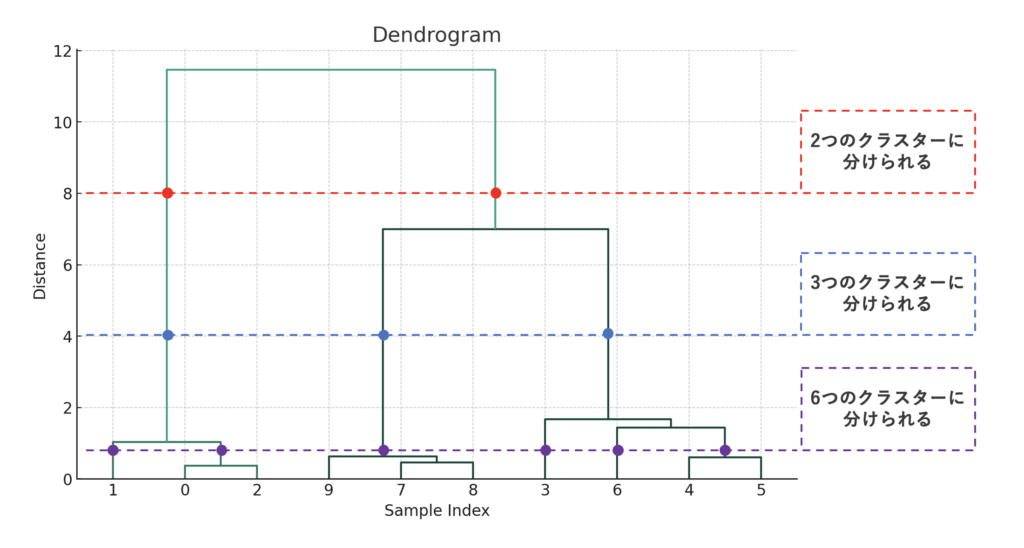
縦軸の「Distance」は要素同士の距離、すなわち「どれだけ似ているか」を表しています。「Distance=8」でクラスターは2つに分けられます。同様に「Distance=4」でクラスターは3つになります。「Distance」とある通り、それぞれどれだけ似ているかを表すために、クラスター間の距離を求める必要があります。距離を求める代表的な方法は、「ウォード法」「重心法」「群平均法」「最短距離法」「最長距離法」などがあります。
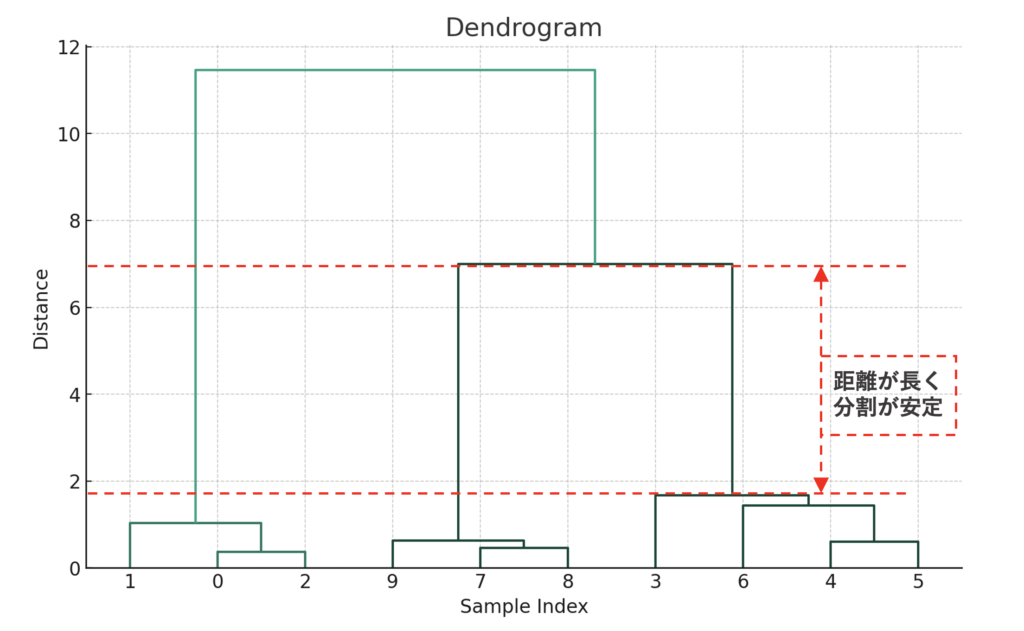
クラスターを分割する際に、個数による観点の他に「安定」もあります。上のグラフのように、「Distance=2」から「Distance=7」まで、どの位置で分割しても、分割されるクラスターは3つとなります。
非階層クラスタリング
非階層クラスタリングとは、あらかじめ何個のクラスターに分類するか決めた上で分類をおこなう手法で、分類に使用する変数がふたつの場合、以下のような散布図で表すことができます。また、代表的な分類手法に「K-means法」があります。

上図の場合、グループ関係や要素間の類似度などを直感的に把握することができます。ただし、グルーピング結果を平面上に可視化できるパターンは、ふたつの変数のみをクラスター分析に使用する場合に限られるという点に注意が必要です。
また上記の散布図は、上下2つのクラスターに分割できそうですし、さらに分割できそうなプロットにもなっています。このようにクラスター数の判断で迷うとき、代表的な手法として「エルボー法」と「シルエット分析」という方法があります。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。クラスター分析による分析の実績などもございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
エルボー法
エルボー法は、それぞれのクラスタ内の誤差平方和(SSE)を計算し、クラスター数とそれぞれの誤差平方和の和をプロットして適切なクラスタ数を判断する手法です。
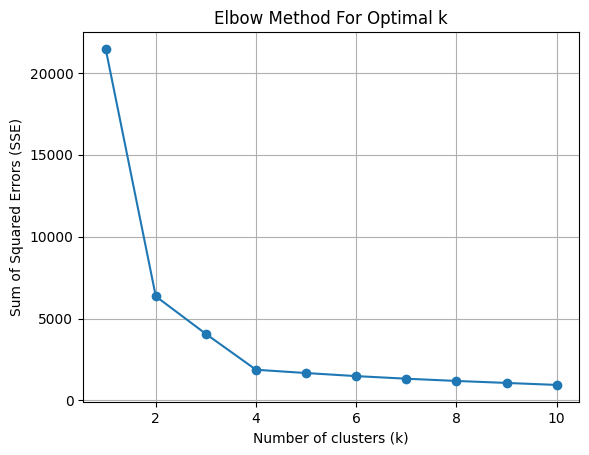
エルボー法は、誤差平方和(SSE)があまり下がらなくなってきたクラスタ数を採用する方法で、この場合クラスタ数は4が妥当と判断されます。

クラスターは4つに分類されている
エルボー法を用いて求めた「クラスタ数=4」で可視化をおこなうと上記のようになります。うまく分類できているようです。
シルエット分析
「シルエット分析」は、クラスタ内の凝集度(クラスタ内データ点同士の集まり具合)と、クラスタ間の乖離度(最も近いクラスタとの離れ具合)を用いて、-1から1までの値を取る「シルエット係数」を算出しておこないます。シルエット係数の値が「1」に近いほど「良いクラスタリング」と解釈され、「-1」に近いほど「悪いクラスタリング」と解釈されています。
このシルエット係数は、データ点ひとつひとつで計算することのできる数値です。以下のような「シルエット図」を描画することで、クラスタ数の判断材料とすることができます。

あるデータの5つのクラスターに対して、シルエット図を描画すると上記のようになります。シルエット係数はクラスタ内での密度が高くクラスタ間の距離が離れていると、「1」に近づきます。一方、クラスタの密度が低く、クラスタ間の距離も近いとシルエット係数は「-1」に近づきます。
上記右側の横棒グラフがシルエット図になります。横軸に各データ点のシルエット係数の値を取ります。その横棒グラフを、クラスタごと・シルエット係数の小さい順に並べることで、上記のようなグラフになります。また赤の点線はすべてのシルエット係数の平均値を表しています。
上記と同じ散布図を用いて、クラスタ数を「3」とした場合、以下のような散布図とシルエット図になります。
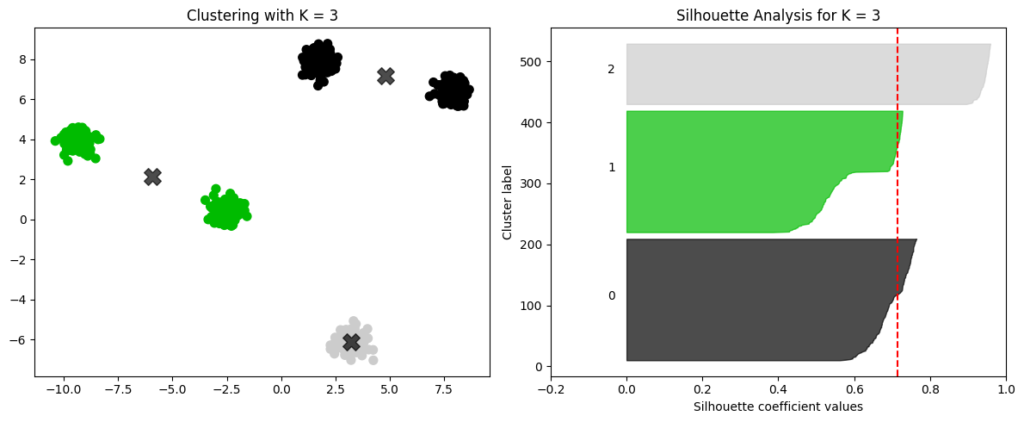
グレーのクラスタは、うまくグルーピングできていることから、クラスタ内のシルエット係数も高くなっていることがわかります。一方黒と緑のクラスタでは、同じクラスタ内でも離れているデータ点同士が存在していることより、シルエット係数はグレーと比較すると高くありません。このように、クラスタが「少ない」とクラスタの密度が小さくなってしまい、シルエット係数も上がらなくなってしまいます。
次にクラスター数を「7」とした場合、以下のような散布図とシルエット図になります。

クラスタ同士が近すぎることでシルエット係数の値がマイナスの数値となるデータ点が存在しています。クラスタによっては、シルエット係数の最大値も約0.5であったり、相対的に低い数値となっています。このように、クラスタを「分けすぎ」ているとクラスタ間の距離が近くなってしまい、シルエット係数も上がらなくなってしまいます。
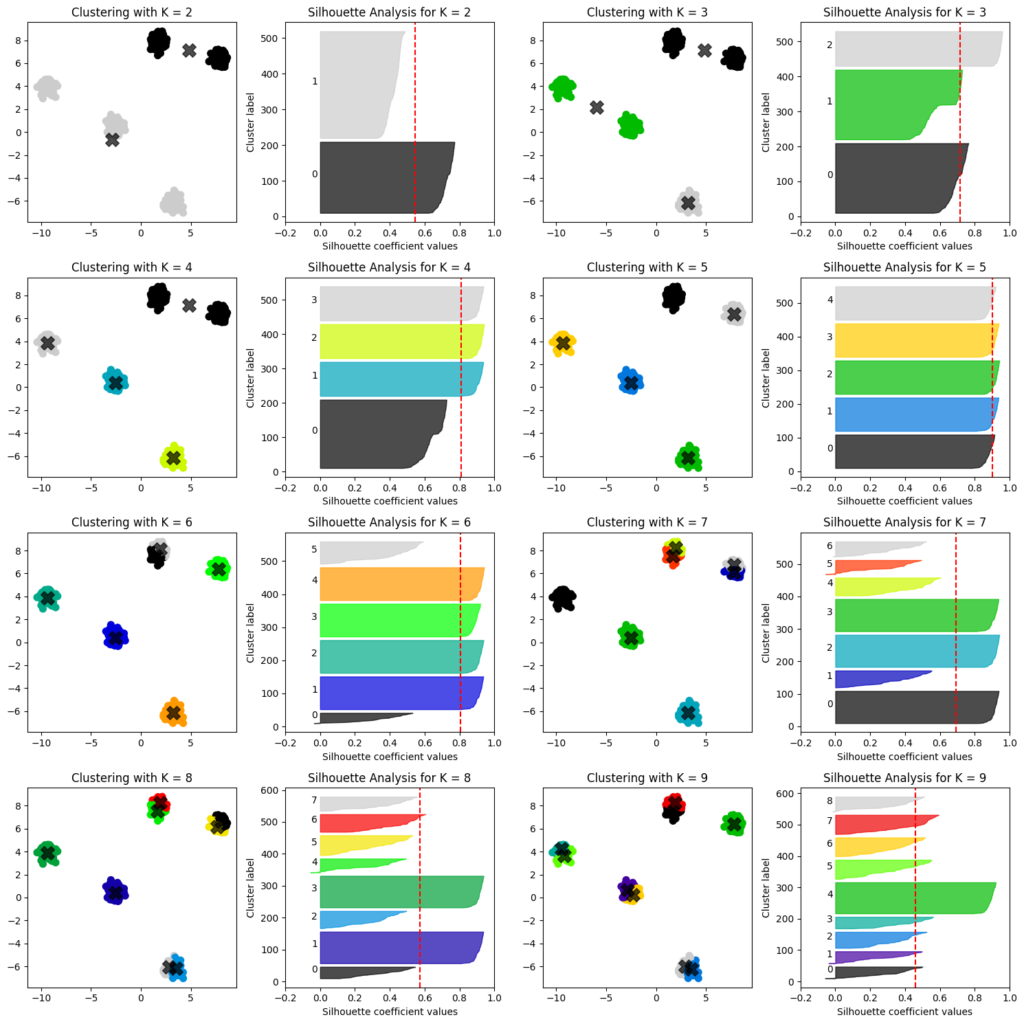
上記の散布図を用いてクラスタ数2~10までのシルエット図を描画しました。クラスタ数の増減によるシルエット図の変化を把握することができます。
必要なデータ
クラスター分析をおこなうために必要なデータは、連続した数値で表すことができる量的なデータです。
一方、「年代」や「性別」などの質的変数(カテゴリカル変数)を量的変数と一緒に扱う場合は注意が必要で、Gower距離を用いてクラスタリングする必要があります。
詳細な計算方法は割愛いたしますが、Gower距離は、量的変数に対する距離計算方法(マンハッタン距離)と質的変数に対する類似度計算方法(Dice係数)を組み合わせて求める手法になります。
クラスター分析のビジネスシーン活用
続いてはビジネスシーンでの活用方法について、それぞれ「階層クラスター分析」「非階層クラスター分析」の2種類を解説いたします。
階層クラスター分析のビジネス活用
マーケティングリサーチの一環として競合サービス(商品)のグルーピングを行う場合の解説をいたします。
まず、クラスタリングするサービスをユーザーアンケートデータや第三者評価データなどから、下表のように定量的に評価します。
| Service | 価格 | 利用者数 | 性能 | 拡張性 |
|---|---|---|---|---|
| Service_1 | 2 | 9 | 6 | 8 |
| Service_2 | 2 | 8 | 5 | 8 |
| Service_3 | 3 | 9 | 7 | 8 |
| Service_4 | 6 | 5 | 7 | 6 |
| Service_5 | 5 | 4 | 7 | 7 |
| Service_6 | 6 | 6 | 5 | 4 |
| Service_7 | 10 | 3 | 9 | 2 |
| Service_8 | 9 | 3 | 8 | 4 |
| Service_9 | 7 | 2 | 10 | 3 |
| Service_10 | 10 | 1 | 8 | 4 |
利用者数:1→少, 10→多
性能:1→低, 10→高
拡張性:1→低, 10→高
上記のデータを階層クラスタリング分析すると、以下のようなデンドログラムを得ることができます。

上記のデンドログラムから、Service_1~3、Service_4~6、Service_7~10が比較的近い距離でまとまっているということがわかります。これよりもクラスタ数を減らすとなると、サービス間の距離が遠くなります。また、クラスタ数を増やそうとすると、サービス同士の距離が近く分割が安定しません。
この例の場合、クラスタは3つと判断するのが妥当と考えられます。
さらにデータを見ていくと、3つのクラスタに共通する要素が見えてきます。
デンドログラムの左側のクラスタは、Service_1~3で構成されています。低価格帯で利用者が多く、性能はほかのサービスより低いものの拡張性の高さが特徴といえます。
デンドログラムの中央のクラスタは、Serivice_4~6で構成されています。中価格帯で利用者数も少ないわけではなく、性能も拡張性もそこそこのクラスタです。
デンドログラムの右側のクラスタは、Service_7~10で構成されています。高価格帯で利用者も限定的、性能はかなり高いものの拡張性は低いことが特徴のクラスタです。
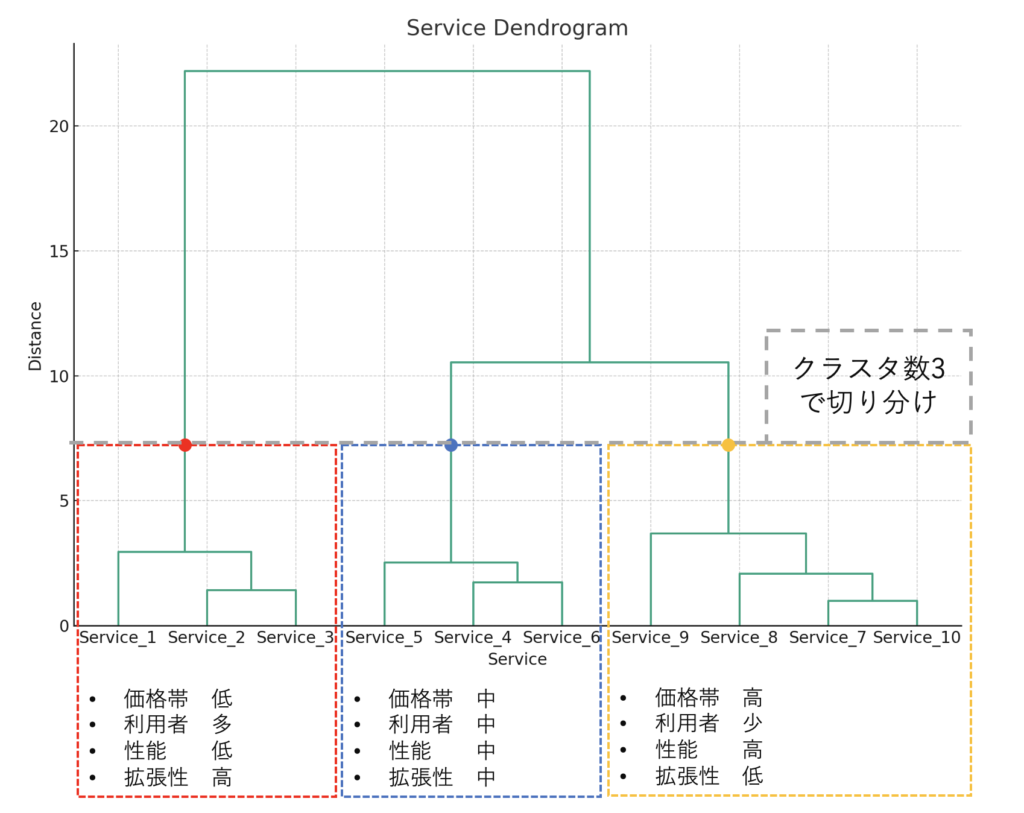
このようにして、分類されたクラスタに対して特徴を解釈することができます。これらの特徴から、自社のサービスがどのポジションを取っていくのか判断するなどして、ビジネスの現場でも活用することができます。
非階層クラスター分析のビジネス活用
自社の顧客データを活用したグルーピングを行う場合の解説をいたします。
自社の顧客のデータで、「いつ購入したか」「どれくらいの頻度で購入したか」「いくら購入したか」のデータがあるとします。これらの特徴を用いた分析を「RFM分析」と呼びます。
こちらの3つの特徴を持った100人分の顧客データは、以下のような形で取り扱います。
| ID | Recency | Frequency | Monetary |
|---|---|---|---|
| 1 | 61 | 7 | 49,810 |
| 2 | 73 | 11 | 24,869 |
| 3 | 33 | 8 | 11,230 |
| 4 | 14 | 8 | 33,969 |
| … | … | … | … |
| 100 | 226 | 8 | 18,191 |
この例における分析では、データに対して概要をつかむこと、そして最終的にはクラスタリングして施策の出し分けができるすることを目的として紹介いたします。
はじめに、顧客データの散布図行列を描画します。
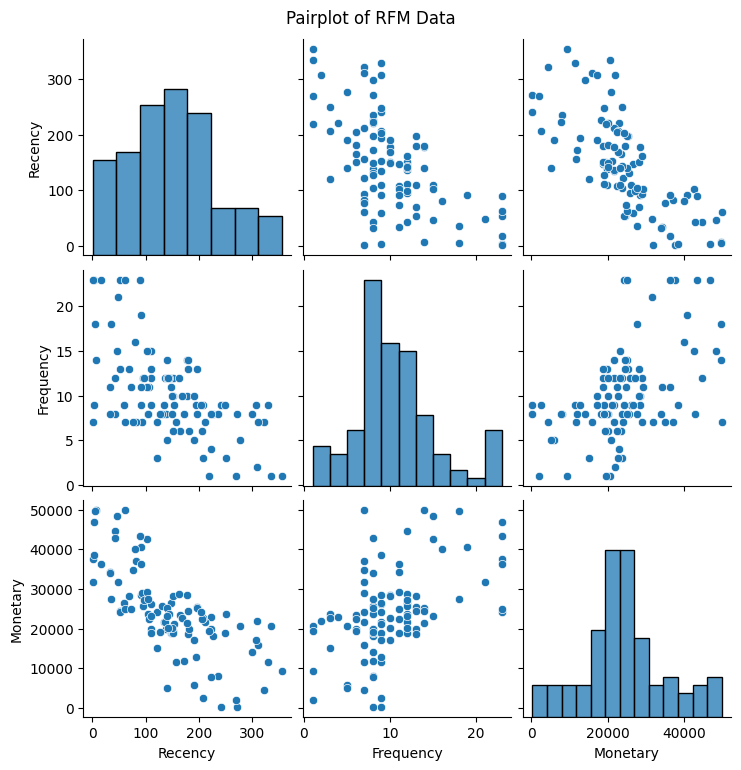
分布をみる限り、各データの中央付近に分布が集まっているような結果となりました。この結果を非階層クラスタリングするために、クラスタ数を決定しなければなりません。ここでエルボー法を使用してクラスタ数のあたりをつけていきます。
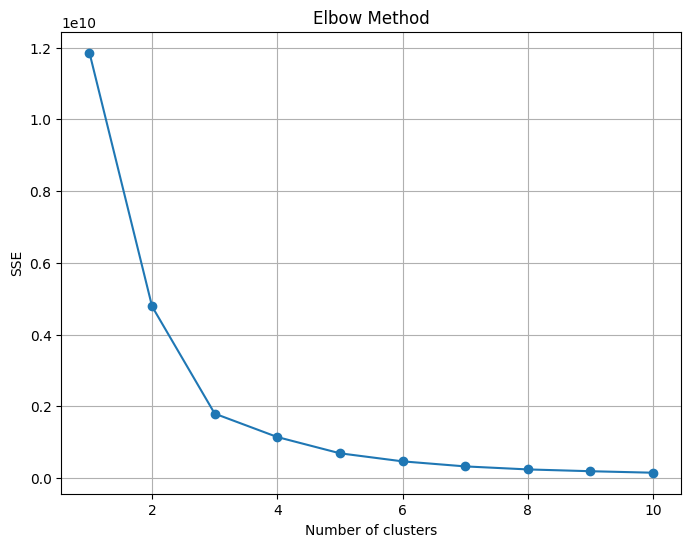
クラスタ数は3~4程度でうまく表現できそうなことがわかりました。ここでまずはクラスタ数3で、再度散布図行列を描画して特徴を把握します。
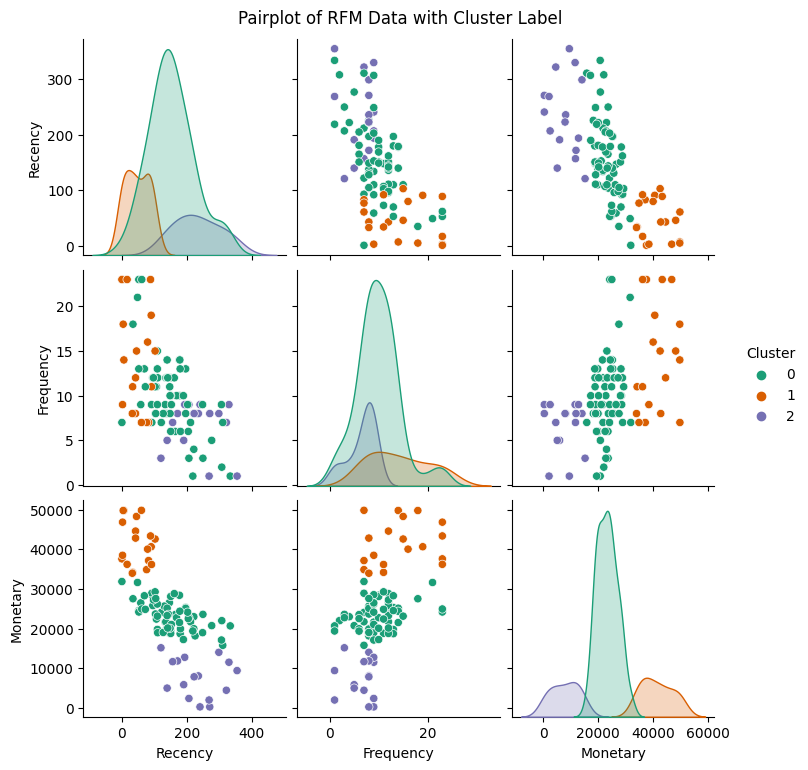
そこそこ分類できていそうです。しかし、「Monetary」に関する可視化を見ると、ほかの変数と比較して、どうにもきれい過ぎる分類結果であると考えられます。
その原因は、スケールがそろっていないことにあります。「Recency」は0~およそ400まで、「Frequency」は0~およそ25まで、「Monetary」は0~およそ60,000まで。これでは、エルボー法に用いている誤差平方和(SSE)は「Monetary」の影響を強く受けてしまいます。
このようなスケールの異なるデータに対しては、平均0、分散1となるように「標準化」をして対処する必要があります。標準化をした結果の散布図行列を再度出してみます。
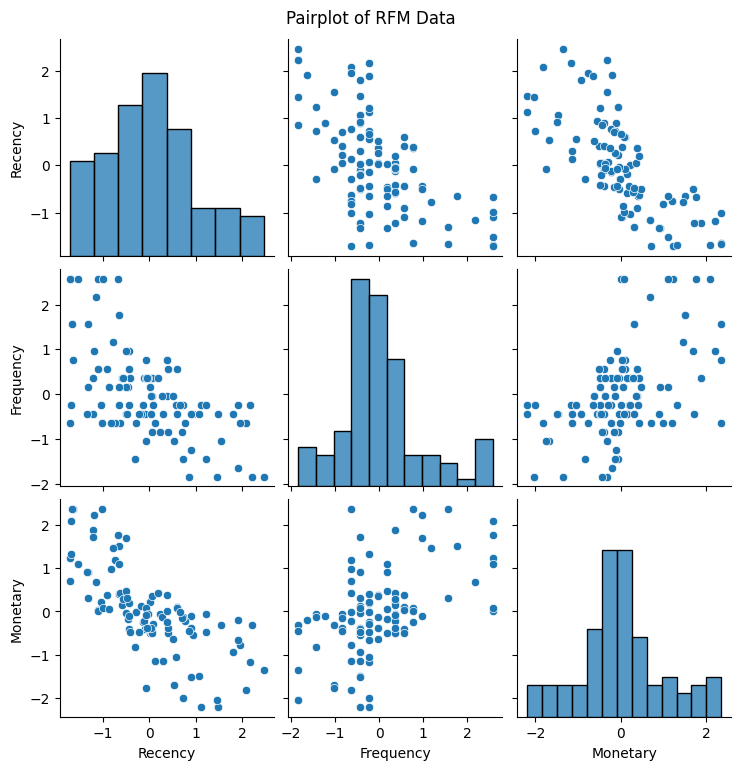
データの特徴を失うことなく、すべての変数でスケールを揃えることができました。再度、エルボー法でクラスタ数のあたりをつけます。
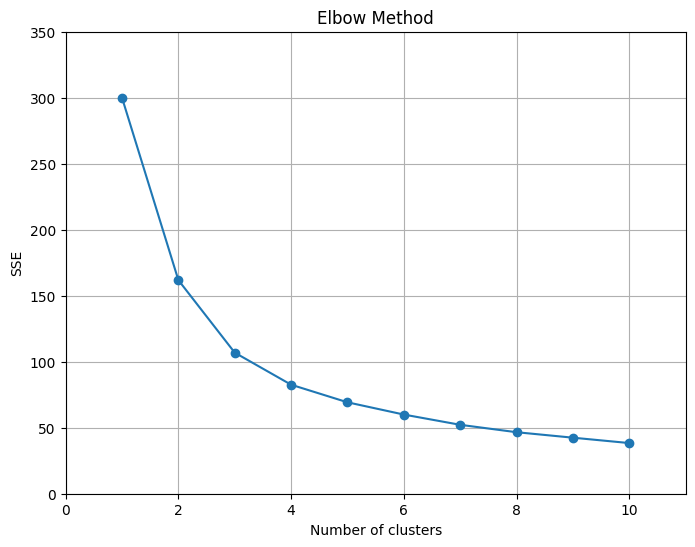
先ほどよりも少しなだらかになりました。この結果より、妥当なクラスタ数を3と判断するとします。その判断に従って、分類されたクラスタのラベルがついた状態で散布図行列にして可視化します。

特徴がつかめそうな形で分類ができました。おおよそロイヤルティの高い顧客(24人)、低い顧客(32人)、その中間のボリューム層(44人)というような形で分類がされました。
この分類からさらに深堀りして、「どのような種類の商品を購入しているか」や「購入している商品の単価はいくらか」などを調査することで、施策の出し分けにつなげることができます。
このようにして、ビジネスの現場でもクラスター分析をおおいに活用することができます。
クラスター分析の注意点
クラスターの考察は必ず主観が入る
クラスター分析の最大の注意点は、「必ず主観が入る」です。
非階層クラスター分析では、「何個のクラスターに分けるか」「○○の要素と××の要素を持つということは、つまり△△と言い換えられる」などが主観の入る余地になります。
階層クラスター分析では、デンドログラム(樹形図)のどこを閾値とするか、などが主観の判断になります。
クラスター分析は解釈の合意を得ながら進めるとともに、人それぞれ解釈が異なる可能性があることを念頭に入れて分析をおこなう姿勢が重要となります。
必ずしも解釈可能な結果になるとは限らない
クラスター分析の注意点として、「必ずしも解釈可能な結果になるとは限らない」ことが挙げられます。むしろエルボー分析やシルエット分析をしても美しい結果が得られないことがほとんどでしょう。
クラスター分析は、想定していた仮説とは異なる分類がされたり、綺麗に分類できていたとしても分類の意味するところを人が解釈できなかったりすることがあります。クラスター分析の結果は、つまるところ数値の計算結果であることから、「必ずしも解釈可能な結果になるとは限らない」のです。
このような注意点があることを念頭に入れ、仮説やドメイン知識に基づく変数選択などの試行錯誤を前提に分析することが重要です。
鎖効果
鎖効果とは、ある距離でクラスタを切ったとしても、特定のクラスタとそれ以外はひとつずつのデータとなってしまう現象のことをいいます。別の表現として、クラスターを広げた際に一つずつクラスターに吸収されてしまうような現象を表します。鎖効果は、クラスター分析においては避けるべき現象のひとつです。
グラフにすると以下のような状態になります。
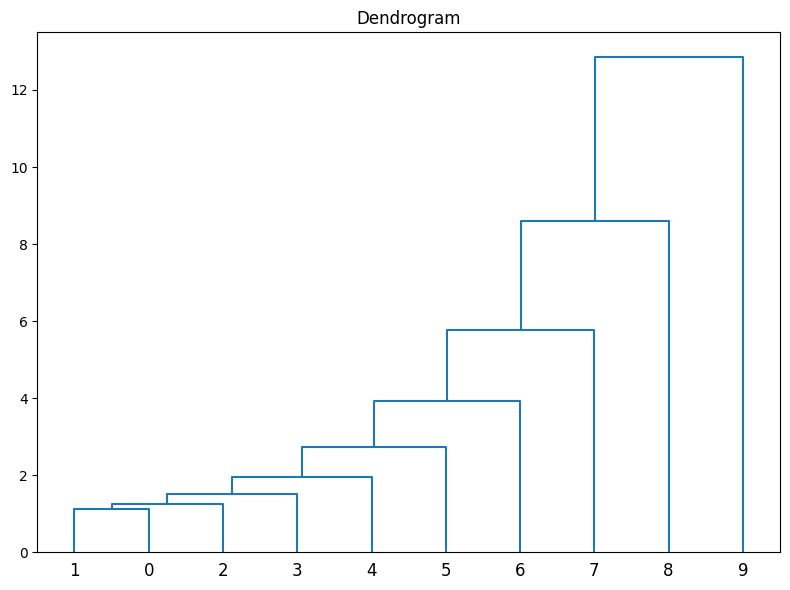
鎖効果は、クラスター間の距離の計算方法を変えることで対処できることもあります。
まとめ
今回はクラスター分析に関する解説をいたしました。本記事のまとめは以下の通りです。
- 階層型と非階層型に分けることができる
- 階層型はデータ数が少ない場合に適していて、非階層型はデータ数が多い場合に適している
- 階層型はあらかじめクラスタ数を決定する必要はないが、非階層型は決定する必要がある
- クラスタ数を決定するための方法として「エルボー法」や「シルエット分析」がある
- クラスターを解釈する際は、主観が入る
クラスター分析の特性や注意点を踏まえた、一歩深い分析の役に立てれば幸いです。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。クラスター分析による分析の実績などもございますのでお気軽にご相談ください。
研究記事も執筆しています
















