お気軽にお問い合わせください
構造方程式モデリング”SEM”とは?ビジネス活用例を徹底解説!

構造方程式モデリング(SEM:Structural Equation Modeling)とは
構造方程式モデリング(SEM:Structural Equation Modeling)とは、観測したデータや観測できない隠れた要因の関係性を把握するために、仮説に基づいて観測データや隠れた要因の関係性をモデル化した上で分析する手法です。
構造方程式モデリングの詳細
構造方程式モデリングを理解する前提として、構造方程式モデリングの構成要素である①パス解析と②因子分析について理解する必要があります。以下、順に説明します。
①パス解析
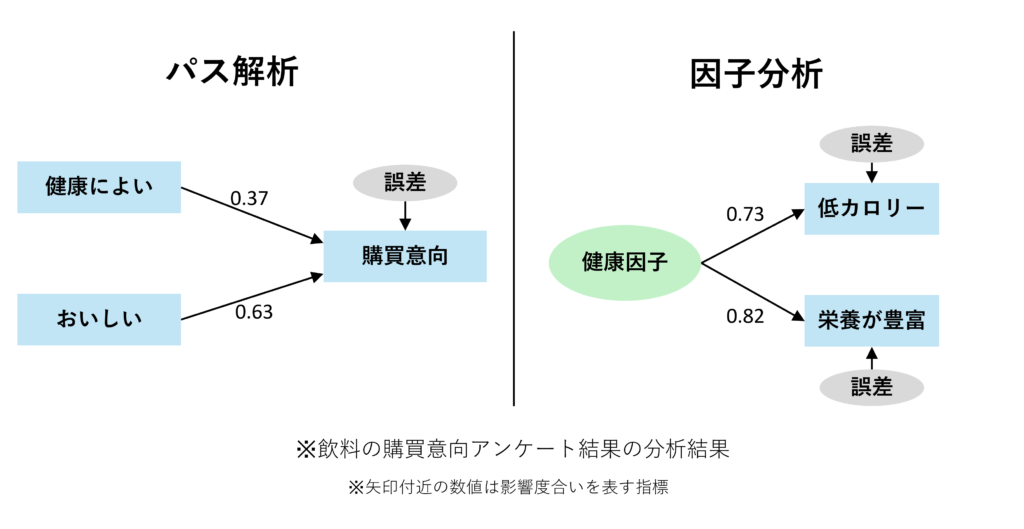
パス解析は、下図左側で示したようなパス図によって変数同士の関係性を表現する分析手法です。矢印は因果の向きを表しており、アンケートで「健康に良い」又は「おいしい」と回答したことが「購買意向」を有している原因となっていることを意味しています。矢印の上の数値は影響の度合いを表しています。
②因子分析
因子分析は、複数の変数に共通する因子を探る手法です。因子とは、観測された変数の背後に存在する潜在的な要因のことを指します。下図右側は、アンケートの回答で「低カロリー」、「栄養が豊富」と答えた人に共通する「健康因子」を表した図になります。パス解析と同様に、矢印の上の数値は「健康因子」による「低カロリー」、「栄養が豊富」という回答への影響度合いを示しています。

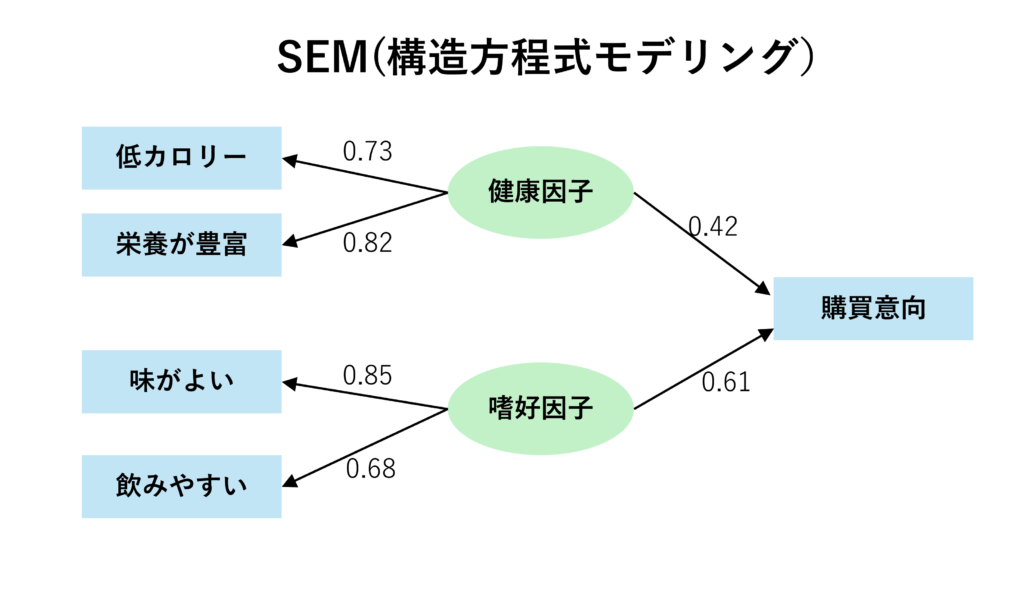
構造方程式モデリングは、上記のパス解析と因子分析を組み合わせたものになります。(下図参照)
パス解析だけでも各項目の購買意向に対する影響を把握することはできますが、「健康因子」や「嗜好因子」を間に挟むことでより実態に即した柔軟なモデリングを行うことができるというメリットがあります。
以下、構造方程式モデリングに使われる用語について説明します。
| 用語 | 意味 |
|---|---|
| 観測変数 | 実際に観測された変数。パス図では、□(四角)で囲って表現する。 |
| 潜在変数 | 直接観測できない変数。主に因子を指す。パス図では〇(丸)で囲って表現する。 |
| パス係数 | パス図の矢印の上に記載している係数。値が大きい程、矢印の方向の指標への影響が大きくなる。標準化を行うことで他指標との相対的な比較が可能。 |
| 適合度指標 | モデルが観測されたデータにどの程度適合しているか測る指標。 |
| AGFI | SEMでよく使われる適合度指標。0~1の間の値になり、1に近い程モデルの精度が良い。0.9以上あると当てはまりのよいモデルと判断されることが多い。 |
構造方程式モデリングによってわかること
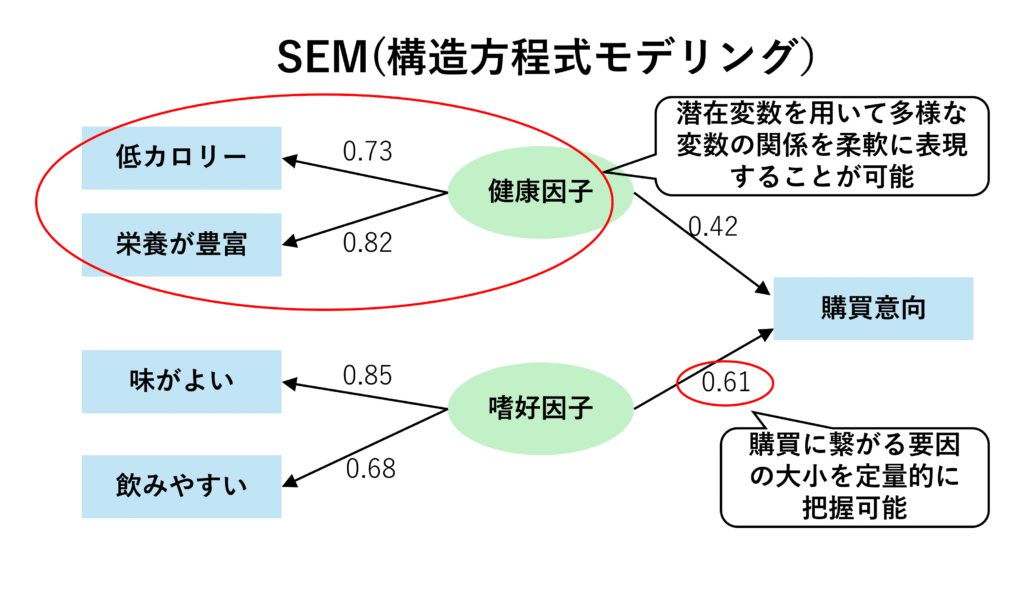
構造方程式モデリングでは、潜在変数を用いて多様な変数の関係を柔軟に表現することや、変数間の影響の度合いを定量的に把握することが可能です。
ただし、パス図は予め分析者が設定する必要があるため、因果関係を探索する用途としてはあまり向いていません。複数のパターンでパス図を作成し、適合度指標を比較することで、変数同士の関係性を探索することも可能ですが、モデルパターンの調整には専門的な知見が必要になります。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。構造方程式モデリングによる分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
構造方程式モデリングと類似した分析手法
構造方程式モデリングと類似した分析手法として、パス解析・因子分析の他に「重回帰分析」があります。
重回帰分析も構造方程式モデリングと同様に変数間の影響の度合いを数値化することができる分析手法になりますが、重回帰分析では一つの変数(目的変数)に対する他の変数(説明変数)の影響しか把握できないのに対して、構造方程式モデリングでは、パス図によって複数の変数同士の関係性を同時に把握できる点が異なります。
以下の表は、構造方程式モデリング(SEM)と類似点を持つ分析手法の違いを比較したものになります。
| 特徴/項目 | SEM | パス解析 | 因子分析 | 重回帰分析 |
| 変数の影響度合いの数値化 | 〇 | 〇 | 〇 | 〇 |
| 潜在変数の有無 | 〇 | × | 〇 | × |
| 説明変数同士の関係 | 〇 | 〇 | × | × |
| 参照記事リンク | 本記事 | – | 因子分析とは?ビジネス活用や注意点を解説! | 重回帰分析とは?数値予測の第1歩! |
必要なデータ
相関を取ることができる量的なデータがあれば分析可能です。よく使われる例としては、アンケート調査データがあります。以下は、企業のブランドイメージに関するアンケート調査データの例になります。
| 回答者ID | ブランド認知度(1〜5) | 信頼性評価 (1〜5) | 製品満足度 (1〜5) | ブランド好感度 (1〜100) |
|---|---|---|---|---|
| 0001 | 5 | 5 | 5 | 95 |
| 0002 | 4 | 4 | 4 | 82 |
| 0003 | 3 | 3 | 3 | 60 |
| 0004 | 5 | 4 | 4 | 90 |
| 0005 | 2 | 2 | 2 | 45 |
| … | … | … | … | … |
以下は、売上と広告費、ウェブ訪問数の推移を表した時系列データです。こちらも同時点のデータで相関を取ることで構造方程式モデリングによって分析することが可能です。
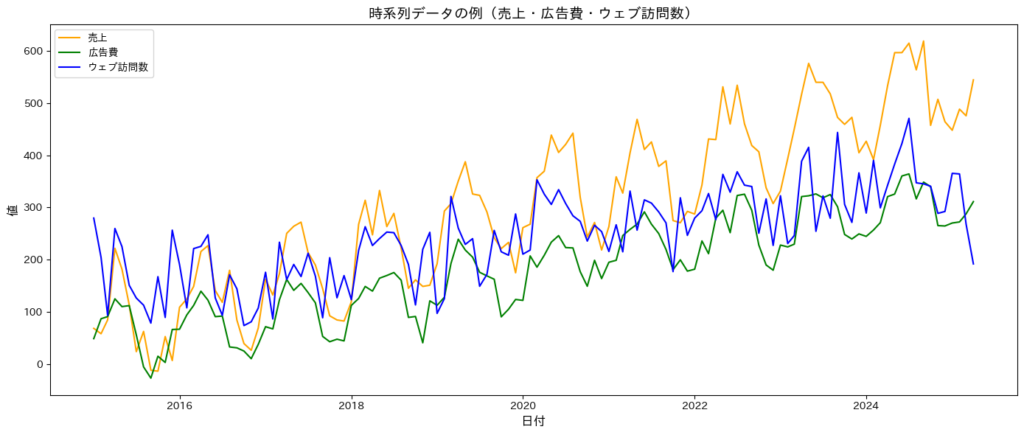
ただし、構造方程式モデリングではあくまで相関のみを考慮して分析するため、基本的には経年で増加する「長期変動・トレンド」や周期的な変化である「季節変動」を捉えることができません。
※トレンドや季節変動を捉えることができる時系列分析は以下の記事を参照ください。
ビジネス活用例
広告データにおける構造方程式モデリングの活用例
広告データに構造方程式モデリングを活用することで、SNS投稿数やオウンドメディアへの流入といった様々な指標同士の関係性や、「認知」・「興味関心」といった測定出来ていない指標による影響を把握することが可能になります。
以下、サンプルデータを用いて構造方程式モデリングの分析の流れを説明します。
初めに分析の目的を決める必要があります。今回の分析目的は、「売上向上のためにはどのような指標を重視すべきか把握すること。」に設定しました。
以下のようなデータを用いて、分析を実施します。
| 年月 | 売上 | 広告予算 | 広告クリック数 | 広告表示回数 | オウンドメディア流入数 | … |
| 2023/01 | 680,000 | 50,000 | 1,300 | 35,000 | 500 | … |
| 2023/02 | 450,000 | 20,000 | 850 | 10,000 | 350 | … |
| 2023/03 | 760,000 | 30,000 | 600 | 25,000 | 400 | … |
| 2023/04 | 620,000 | 40,000 | 300 | 15,000 | 200 | … |
| … | … | … | … | … | … | … |
データの前処理として、以下の2点を確認した上で対応する必要があります。
- 欠損の有無の確認
欠損値がある場合には、そのままではモデルを構築することができず、欠損を埋める処理が必要になる場合があります。 - 多重共線性の確認
多重共線性とは、説明変数の間に高い相関関係があることを意味します。
構造方程式モデリングではパス係数の推定に一部重回帰分析が使われているため、非常に高い相関関係にある変数をパス図に組み込む場合、パス図次第ではパス係数の推定が上手く行かなくなる場合があります。そのため、事前に「相関分析」などで変数同士に高い相関関係がないか確認する必要があります。
相関分析については以下の記事で解説しています。

モデルを構築するためには、分析者がパス図を設定する必要があります。
今回は、潜在変数として、「認知」・「興味関心」を設定した上で、ドメイン知識に基づき初回のパス図を設定しました。その後、パス図を微調整した上で適合度指標を確認しながら複数のモデルを構築しました。
モデル選択の際には、基本的には適合度指標を比較して高いものを選択しますが、ある程度ドメイン知識があり、どのモデルも適合度指標に大きな差がない場合には、ビジネス感覚と照らし合わせて最も妥当と思われるパス図となっているモデルを選択する場合もあります。
今回は、適合度指標のAGFIが最も良いパス図を選択しました。最終的に選定したモデルが下画像になります。※パス係数は標準化しています。
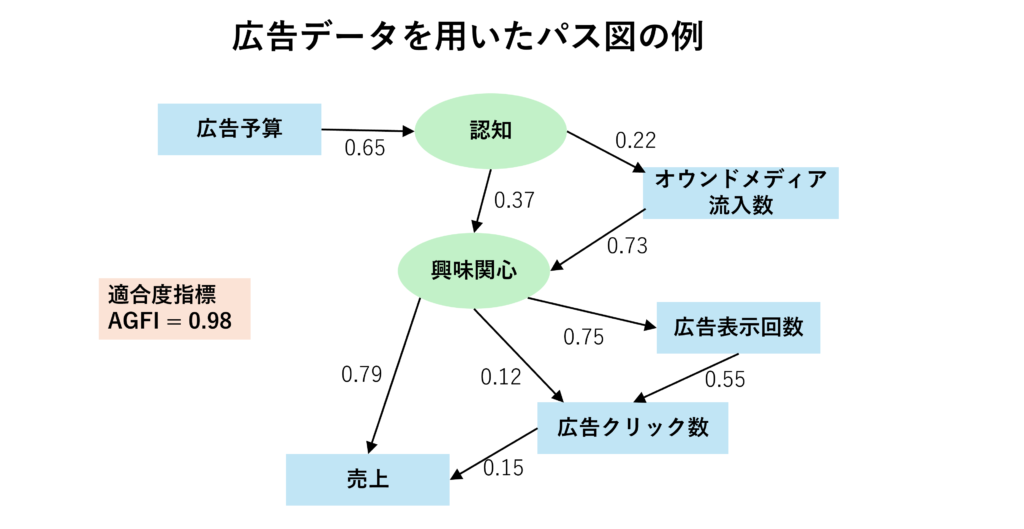
こちらのモデルの解釈ですが、まず、適合度指標であるAGFIが0.98となっており、信頼度が高いモデルであることが分かります。また、売上との関連では、広告のクリック数よりも「興味関心」の方が関連が強く、広告クリック数の増加を目指すよりも、「興味関心」との関連が強いオウンドメディア流入数の増加に力を入れる方が売上向上につながりやすいと解釈することが可能です。
広告データに関しては、時系列モデルであるMMM(マーケティングミックスモデリング)の手法があり、媒体別の広告効果を検証する場合等には、組み合わせて分析を行うことでより精度の高い分析を行うことが可能です。

当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。構造方程式モデリングによる分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから
そのほかのビジネス活用事例
アンケート調査での活用例
構造方程式モデリングでは、例えば男性と女性に分けてモデリングをすることで性別による差異を見ることが可能です。また、競合企業に関するアンケート調査も同時に行っている場合には、競合と自社の比較を行うことも可能です。ただし、同じ構造でモデリングを行う場合には、ドメイン知識や適合度指標のスコアを踏まえて、モデル構造自体が同一であることを事前に確認する必要があります。
以下の例は、冒頭で挙げた飲料のアンケート結果について、モデル構造が同一であることを前提として企業別に構造化モデリングをおこなったものになります。
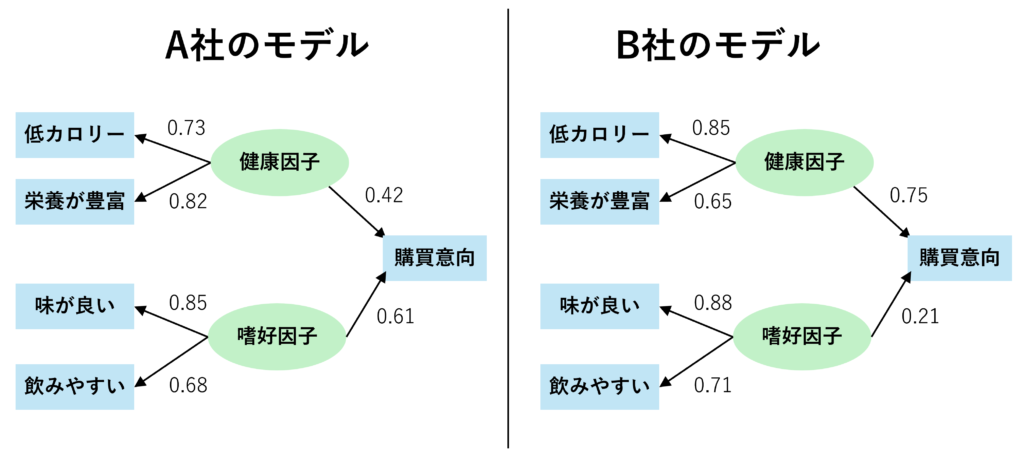
上記のモデルの「購買意向」に繋がる2本の矢印を見ていくと、A社のモデルでは健康因子(0.42)よりも嗜好因子(0.61)の方がパス係数が大きく、A社は健康よりも嗜好に関するイメージが購買意向に影響しやすいことが分かります。一方で、B社のモデルでは、健康因子(0.75)の方が嗜好因子(0.21)よりもパス係数が大きく、嗜好よりも健康に関するイメージの方が購買意向に影響しやすいことが分かります。
注意点としては、各モデルの「健康因子」から左に伸びている矢印のパス係数が異なっているため、それにより因子自体の解釈が変わることになります。上図の「健康因子」では、A社のモデルでは「低カロリー」(0.73)より「栄養が豊富」(0.82)の方が影響が若干強い健康因子であるのに対して、B社のモデルでは、「栄養が豊富」(0.65)より「低カロリー」(0.85)の方が影響が若干強い健康因子となっています。このようにして影響を与える因子のパス係数の大小が異なる場合には因子(潜在変数など)自体の解釈が変わることになります。(上図の例では、B社の方はA社と比較してカロリーを重視した健康因子となっています。)
注意点
パス図を予め設定する必要がある
構造方程式モデリングを実施する際には、予め分析者がパス図における変数の数や矢印の向きを設定する必要があるため、ドメイン知識を基にした因果関係に関する仮説が必要になります。適合度指標等を用いて、パス図を微調整しながら最も当てはまりが良いパス図を探索的に作成することは可能ですが、探索には時間を要するため、おおまかなパス図は事前に設定する必要があります。
非線形な関係にあるデータは適さない
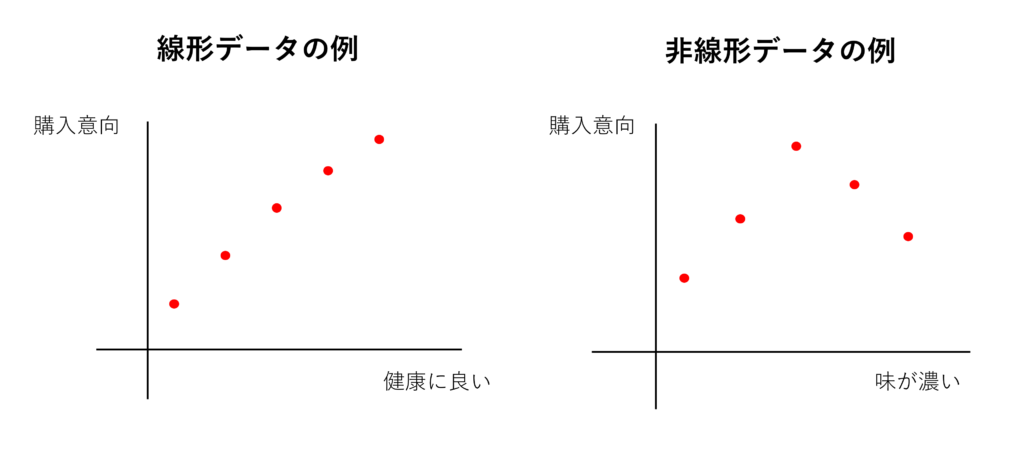
構造方程式モデリングで変数の関係性を表す係数は、変数同士が線形な関係(一方の値が増加した場合に、もう一方が必ず増加又は減少する関係)にあることを前提としているため、非線形な関係性にあるデータの場合には適さないので注意が必要です。
例えば、下図右側のように、ある程度までは「味が濃い」という指標が高い方が購入意向が高くなりますが、一定の値を超えるとむしろ購入意向が下がるような場合には、関連がないという結果になってしまいます。
セレクションバイアスに注意する
モデルに組み込むデータにバイアスがある場合には、モデルもバイアスの影響を受けることになるため、注意が必要です。例えば、アンケート調査データにおいて、商品を購入した人のみが調査対象の場合には、構造方程式モデリングで得られる結果も商品を購入した人に対する結果であり、商品を売り出したい未購入層に関する示唆は得られないことになります。セレクションバイアスへの対処法として、データ入手時に調査対象をランダムに設定することでバイアスが生じないようにすることが必要になります。
一定のデータ量が必要になる
パラメーターを推定する際に、サンプルサイズが小さい場合、誤差や外れ値の影響を強く受けることになり、パラメータ推定結果が安定しないことになります。以下のイメージ図のように、サンプルサイズが大きい場合は外れ値データを追加してもパス係数は大きく変わらないのですが、サンプルサイズが小さい場合には外れ値データによってパス係数が大きく変動してしまうことがあります。
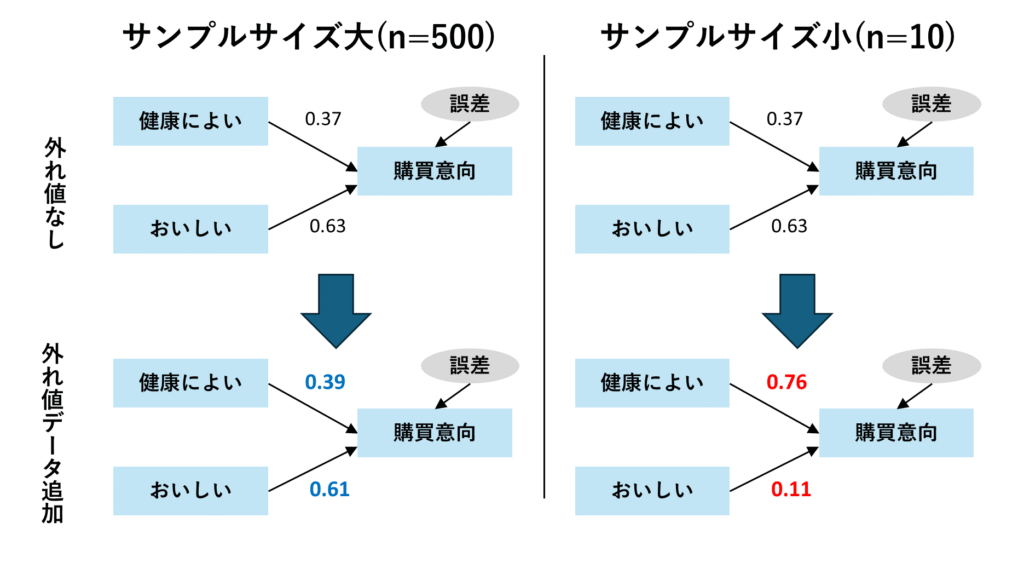
また、構造方程式モデリングでは、パス係数や誤差項といった多数のパラメータを同時に推定してパス図を構築するため、パス図の構造が複雑になるほどパラメータ数が多くなりデータ量を確保する必要性が高くなります。
まとめ
今回は、構造方程式モデリング(SEM)の解説を行いました。
構造方程式モデリングは、複数の指標同士の関係性を統合的に解釈する分析手法であり、実際に観測して得られたデータだけでなく、分析者が設定した潜在変数も扱うことができる点が優れています。ただし、事前に分析者でパス図を設定する必要があり、因果関係を探索することが難しいことなどに注意する必要があります。
構造方程式モデリングの特性や注意点を踏まえた、一歩深い分析のお役に立てれば幸いです。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。構造方程式モデリングによる分析実績も多数ございますのでお気軽にご相談ください。
ご相談・お問い合わせはこちらから














