Index
はじめに
データソリューション事業部の今川です。
本記事では、「Predicting COVID-19 hospitalisation using a mixture of Bayesian predictive syntheses」という論文で紹介されたMBPS(混合ベイズ時系列結合)について解説します。
MBPSは「Mixture of Bayesian Predictive Syntheses」の略で、複数の時系列予測モデルを統合し、類似する動態を持つ時系列をクラスタリングすることで予測精度を高める方法です。複数のモデルから得られた予測分布をベイズ的に統合し、その中で似た動きをする時系列をまとめて1つのクラスタとして扱います。このアプローチは、複雑で変動が激しいデータに対して特に有効です。複数のモデルを組み合わせることで単一モデルでは対応しきれない変動を捉え、さらにクラスタリングによって関連するデータ間で情報を共有することで、より正確な予測を可能にします。
前半部分ではMBPSの概要を、後半部分ではMBPSを応用して各国の金融時系列データを予測して、従来の時系列予測モデルとの比較をしていきます。
1.論文紹介
本論文では、COVID-19パンデミック時の入院患者数や隔離者数の予測をMBPSによって実証評価しています。日本の47都道府県(2020年5月7日〜2022年11月23日)と韓国の17自治体(2020年8月1日〜2021年11月30日)のデータを使用しています。
パンデミックは新たな変異株や政策介入によって動態が大きく変化し、単一のモデルでは一貫した予測が困難でした。MBPSは複数の予測モデルを組み合わせ、類似する動態を持つ時系列をクラスター化することで、予測精度を向上させています。
結果として、MBPSは予測精度(累積絶対誤差)や不確実性(95%予測区間のカバレッジ)で他の手法を上回ることが証明されました。
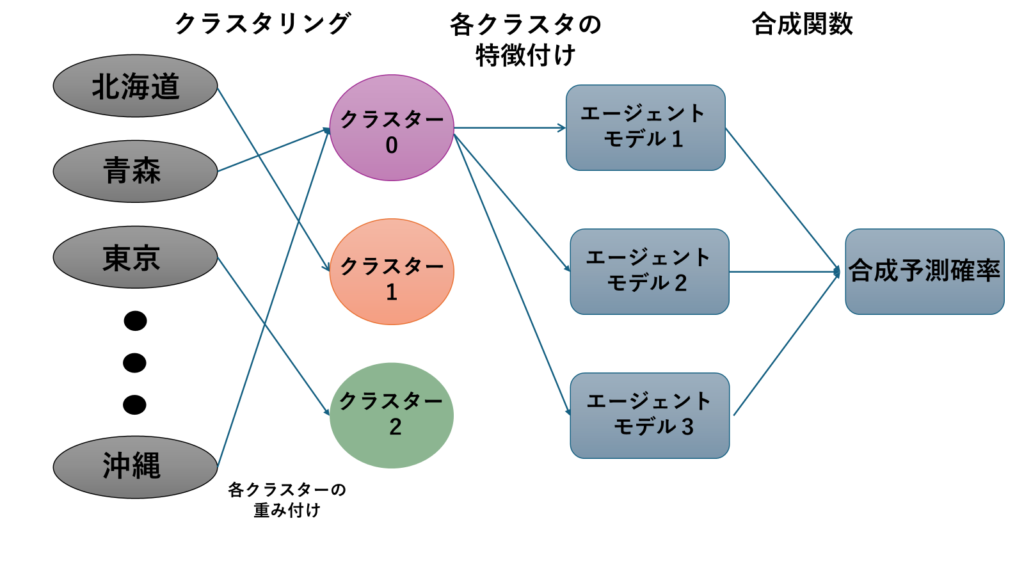
2.MBPS(混合時系列結合)
MBPSは、複数の時系列予測モデル(エージェントモデル)を組み合わせて予測を行うベイズ予測合成(BPS)の拡張です。各時系列ごとに複数の「エージェントモデル」から得られた予測値を組み合わせ、その中で似た予測傾向を持つ時系列をクラスタ化します。
具体的には、各エージェントモデルが出す予測を「重み付き」で合成し、その重みは同じクラスタ内の時系列で共通になります。このため、例えば「政策変更に敏感な時系列」や「季節性が強い時系列」など、似た特性を持つデータをまとめて扱うことができます以下にMBPSの重要な特徴を説明します。
2.1 ベイズ予測合成(BPS)
- 複数のエージェントモデル(時系列予測モデル)から得られる予測分布を統合するベイズフレームワーク。
- エージェントモデル \(j\) の予測分布を \(h_{tj}(f_{tj})\) とした場合、合成分布は以下で表されます: ここで \(α(yt∣ft,Φt)\) は合成関数、\(Φt\) は重みなどのパラメータ。
$$ p(y_t | \Phi_t, H_t) = \int \alpha(y_t | \mathbf{f}t, \Phi_t) \prod{j=1}^J h_{tj}(f_{tj}) \, d\mathbf{f}_t $$
数式
時系列データを複数のクラスターに分割し、各クラスター内でエージェントモデルの重みを統一。
$$ p(y_{it} | \Phi_t, H_{it}) = \int \left[ \sum_{k=1}^K \pi_k \alpha(y_{it} | \mathbf{f}{it}, \Phi{tk}) \right] \prod_{j=1}^J h_{itj}(f_{itj}) \, d\mathbf{f}_{it} $$
変数
- \(y_{it}\):時刻\(t\)における観測データ\(i\)
- \(H_{it}\):時刻\(t\)のデータ履歴またはエージェントモデルによる予測分布
- \(\pi_k\):クラスター\(k\)の混合係数(事前確率)
- \(\alpha(y_{it} \mid \mathbf{f}{it}, \Phi{tk})\):クラスター\(k\)における合成関数で、データ\(y_{it}\)が与えられた潜在因子\(f_{it}\)とクラスター特有パラメータ \(Φ_{tk}\) に基づいて計算される確率
- \(\Phi_{tk}\):クラスター\(k\)のパラメータベクトル(例:重み\(θ\)など)で、時間 \(t\) に依存
- \(\mathbf{f}_{it}\):エージェントモデル\(j\)の潜在予測因子の集合
- \(h_{itj}(f_{itj})\):エージェントモデル\(j\)から得られる\(t\)時点での予測分布
利点
- 多変量モデルの必要性を排除(各時系列をクラスター化して単純な統合を実現)。
- クラスター内で情報を共有し、計算コストを削減。
例: ポアソン分布を用いたMBPS:
$$ y_{it}∣z_i=k,\boldsymbol{\theta}{tk}, \mathbf{f}{it} \sim \text{Poisson}(\lambda_{it}), $$
$$ \lambda_{it} = \exp(\boldsymbol{\theta}{tk}^\top \mathbf{F}{it}), $$
\(z_i\): データ \(i\) のクラスター割り当て。
MBPSが優れている理由
- 複数モデルの組み合わせ:MBPSは複数のモデルを組み合わせるため、単一のモデルよりも変化に強いです。
- クラスタリングの活用:似た動きをする時系列をまとめて扱うことで、少ないパラメータで効率的に予測を行えます。
- 不確実性への対応:COVID-19のように予測が困難なデータでも、複数のモデルを組み合わせることで予測の不確実性を減らせます。
3.複数か国での金融時系列予測
今回の目的は、MBPSモデルと各エージェントモデルの予測指標を比較し、MBPSの精度を検証することです。MBPSモデルの実証には、37か国の経済指標を用いてTOPIX株価を予測しました。金融時系列データを用いた理由は、これらのデータに空間的な相関が存在すると考えられているためです。検証の流れは以下のとおりです。
- データの整備
- 空間相関の確認
- 時系列クラスタリング
- エージェントモデルの選定
- MCMC(マルコフ連鎖モンテカルロ法)による推定
- サンプリングを用いた予測
- 各エージェントモデルとの比較
この手順に沿って、MBPSモデルの有用性を検証します。
各国の金融時系列データ詳細
今回使用したデータは37か国の経済指標終値になります。実データではクラスタリングが難しいため、正規化を行います。
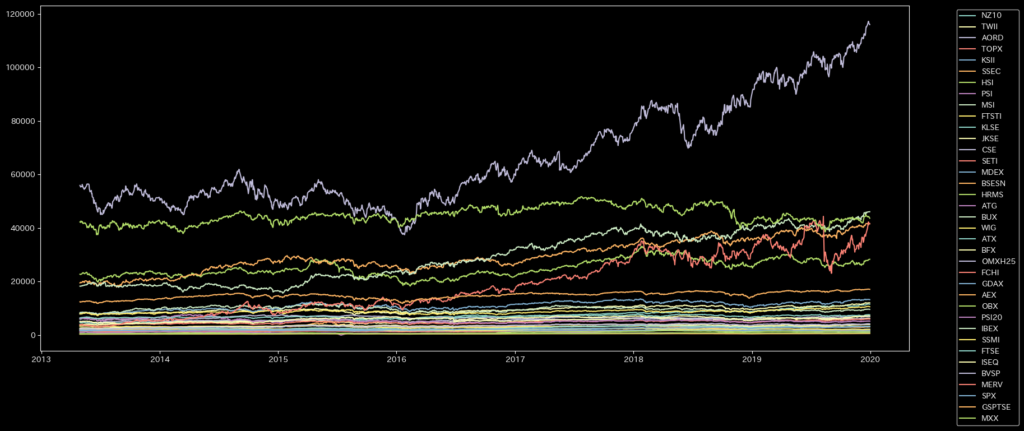
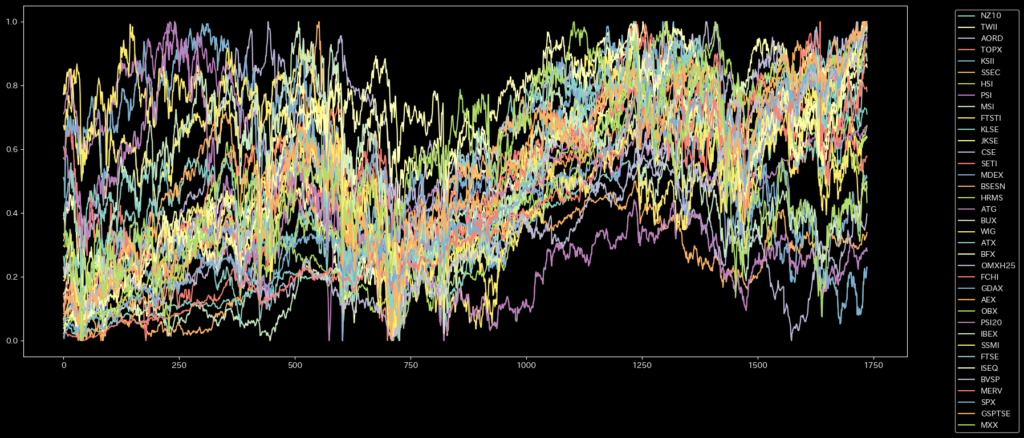
金融時系列データの空間相関
空間相関を最小全域木を使って可視化していきます。
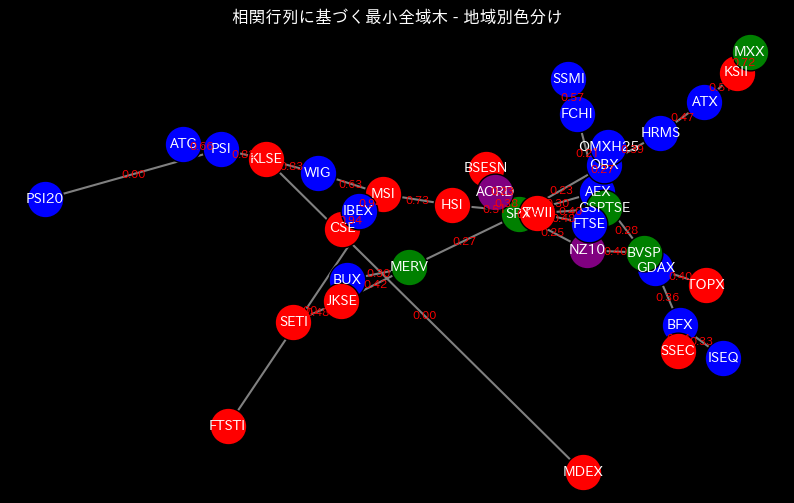
最小全域木は相関が大きいものほど近くなる性質があります。すなわち、ノードが近いほど時系列データは似た性質を持っています。
アジアとヨーロッパ以外の国はサンプル対象の国が少ないため分かりにくいですが、アジアとヨーロッパでは、大州ごとで似た性質があることが分かります。
時系列クラスタ
MBPSモデルの性質上、クラスタ数をモデリングの前に予め決めておく必要があります。そのためエルボー法によるクラスターの数の計算を行います。
エルボー法とは、各点から割り当てられたクラスタ中心との距離の二乗の合計をクラスタ内誤差平方和(SSE)として計算します。 クラスタ数を変えて、それぞれのSSE値をプロットし、「肘」のように曲がった点を最適なクラスタ数とする方法です。 また、SSEが小さいほど歪みのない良いモデルであり、うまくクラスタリングできていることになります。
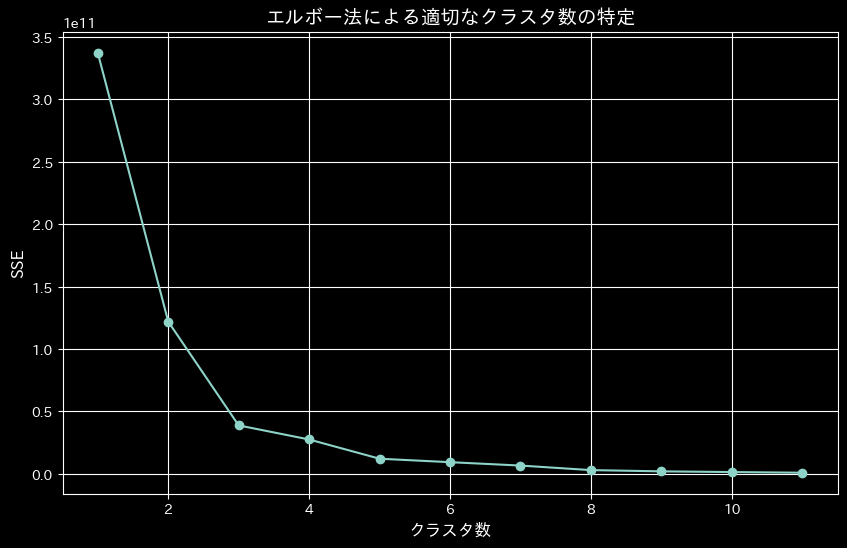
n_clusters=3で肘のように曲がっているので、今回はクラスタ数3でMBPSを設定します。 ただし、一般的にエルボー法ではこのようにはっきりと曲がりがある場合は少なく、あまり精度はよくないようです。また、クラスタ数を多くすると、当然SSEの値は小さくなりますが、計算量が多くなり実行に時間がかかります。
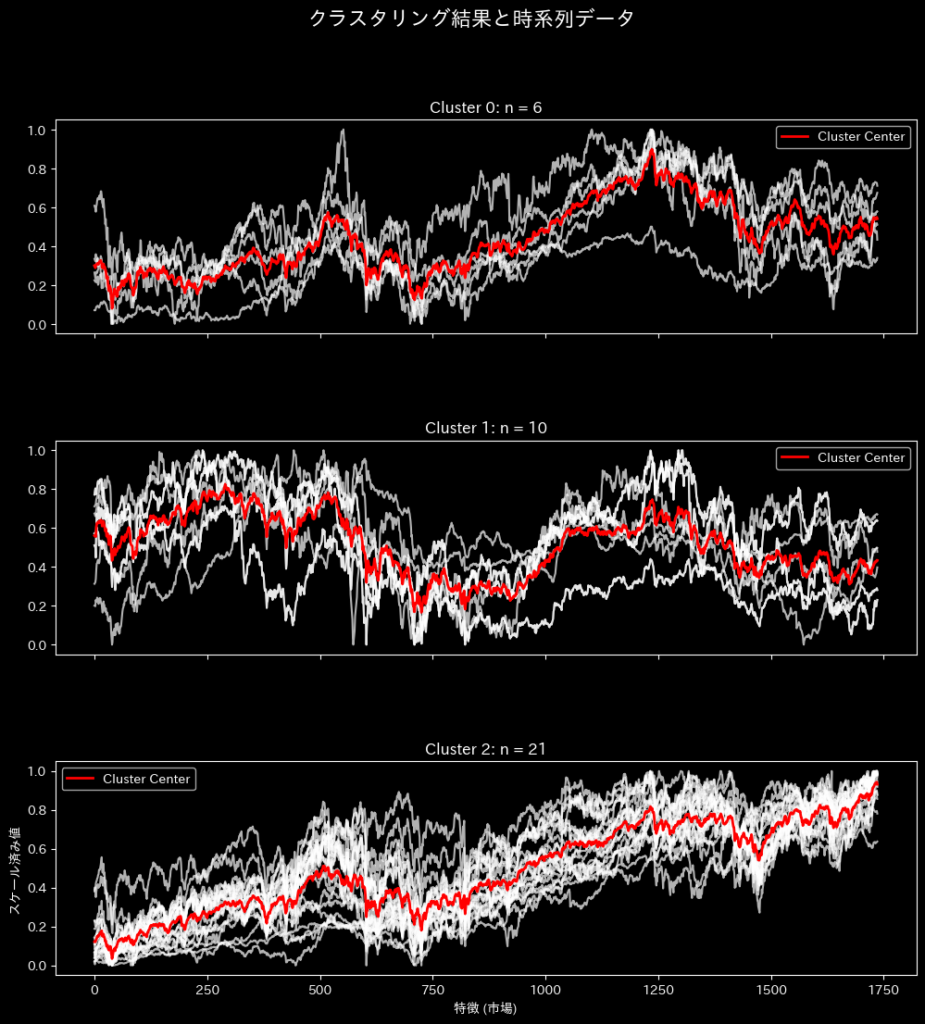
クラスター数を3に設定した場合、今回使用したデータでのクラスタリング結果は下記のようになります。
使用したエージェントモデル
今回使用した時系列予測モデルは以下の3つになります。
ARIMA(自己回帰和分移動平均モデル)
時系列データの傾向や周期性、過去の誤差を利用して将来を予測するモデル。
- シンプルで理解しやすい。
- 季節性やトレンドのあるデータに強い。
- 統計的に確立された手法で、多くのツールでサポートされている。
一般化加法ポアソン回帰モデル(GAM)
非線形な関係を複数の平滑関数で表現し、ポアソン回帰でカウントデータを予測するモデル。
- 複雑な非線形パターンを柔軟に捉えられる。
- カウントデータに適しており、感染者数や来訪者数などに活用できる。
- 過学習を防ぎつつ、多様な要因を組み込める。
ランダムフォレスト
多数の決定木を組み合わせて予測を行うアンサンブル学習の一種。
- 高い予測精度と頑健性(外れ値やノイズに強い)。
- 特徴量の重要度を評価でき、要因分析にも役立つ。
- 非線形な関係や複雑なデータ構造に適応可能。
この3つは、それぞれ異なる強みを持っているため、MBPSのようなモデルで組み合わせると、より信頼性の高い予測が可能になります。
パラメータ説明
1. theta (クラスタ特性のパラメータ):下図の上側
theta は、各クラスタを特徴付けるパラメータです。エージェントモデル間でどの程度影響を受けるかを示します。
2. pi (混合係数):下図の下側
pi は、クラスタ(または状態)に対する確率的な重みを表すパラメータです。これは「各クラスタの所属確率」として解釈できます。具体的には、MBPSモデルでデータ点がどのクラスタに属するかの確率を示しています。pi の値が高いクラスタに、データが多く割り当てられる可能性があります。
pi[0], pi[1], pi[2] はそれぞれ、クラスタ 0、1、2 の混合係数です。例えば、pi[0] = 0.26 は、クラスタ 0 がデータに占める割合が 26% であることを意味します。
収束結果
MBPSモデルのコードは下記の通りです。
def mbps_model(data, n_clusters, n_agents):
"""MBPS モデル: MCMC によるサンプリング"""
n_series, n_time = data.shape # 国数 × 時間
# クラスタの混合重み(Dirichlet 分布からサンプリング)
pi = numpyro.sample("pi", dist.Dirichlet(jnp.ones(n_clusters)))
# 各系列(国)ごとのクラスタ割り当て(Categorical 分布)
with numpyro.plate("series", n_series):
z = numpyro.sample("z", dist.Categorical(pi)) # 形状: (n_series,)
numpyro.deterministic("z_samples", z)
# 各クラスタごとのエージェント重み(正規分布)
theta = numpyro.sample(
"theta", dist.Normal(0, 1).expand([n_clusters, n_agents]).to_event(2)
) # 形状: (n_clusters, n_agents)
# 各時点におけるエージェントモデルの予測値を計算
agent_preds = jnp.array([
[model(series) for model in agent_models] for series in data
]) # 形状: (n_time, n_agents)
# クラスタ割り当てに基づき、theta を取得
theta_z = theta[z] # 形状: (n_series, n_agents)
# λ(Poisson 分布の平均パラメータ)を計算
lambda_mean = jnp.exp(jnp.sum(theta_z * agent_preds, axis=-1))
lambda_mean = jnp.maximum(lambda_mean, 1e-5) # 数値的な安定性を確保
# 観測データの尤度(Poisson 分布)
with numpyro.plate("series", n_series):
numpyro.sample("y_obs", dist.Poisson(lambda_mean), obs=data[:, -1])
mean std median 5.0% 95.0% n_eff r_hat
pi[0] 0.26 0.23 0.18 0.00 0.67 74.07 1.00
pi[1] 0.36 0.28 0.30 0.01 0.78 102.52 1.03
pi[2] 0.38 0.26 0.33 0.04 0.81 71.53 1.01
theta[0,0] -0.32 0.86 -0.34 -1.60 0.90 72.19 1.00
theta[0,1] 0.05 0.89 0.01 -1.16 1.65 90.02 1.02
theta[0,2] -0.13 0.74 -0.21 -1.46 0.98 64.04 0.99
theta[1,0] 0.01 0.79 0.04 -1.26 1.18 95.43 0.99
theta[1,1] -0.15 0.99 -0.12 -2.03 1.21 31.46 1.00
theta[1,2] -0.43 0.80 -0.45 -1.86 0.68 56.19 0.99
theta[2,0] -0.15 0.89 -0.22 -1.40 1.37 71.59 0.99
theta[2,1] -0.24 0.95 -0.08 -1.80 1.06 71.45 0.99
theta[2,2] -0.08 0.95 -0.05 -1.62 1.26 59.52 1.00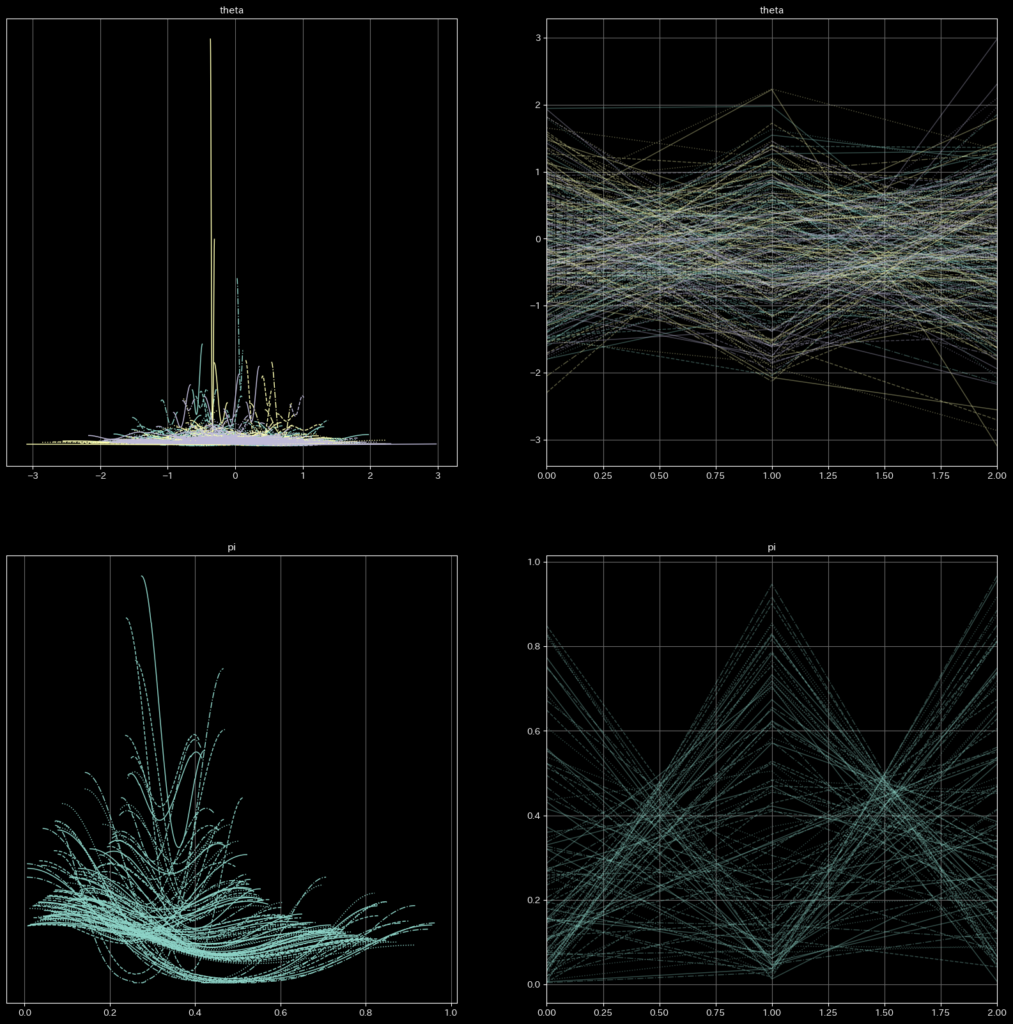
今回の結果から、r_hat値はすべて0.99〜1.03の範囲内に収まっており、一般的に「1.1以下で収束している」と判断される基準を満たしていることが確認できます。ただし、標準偏差(std)が非常に大きいため、予測時の95%信頼区間が広がり、予測の不確実性が高くなることが懸念されます。
また、合成重み(theta)の結果は、前半の数字がクラスタのインデックス、後半の数字がエージェントモデルのインデックスを示しています。今回使用したエージェントモデルは以下の通りです:
- ARIMA
- GAM(一般化加法モデル)
- ランダムフォレスト
結果
実験設定
今回使用したデータは37か国の時系列データ(2013年1月1日~2019年12月31日)
- 学習データ:37か国(TOPIXを含む)2013年1月1日~2018年12月31日の6年間の終値
- テストデータ:TOPIX2019年1月1日~2019年12月31日の1年間の終値
コード
MCMCのサンプリング結果をもとに、将来の予測をシミュレーションするコードは以下のようになります。
def forecast(mcmc_samples, z_samples, test_data, agent_models):
"""
MCMC のサンプルと事後分布の z を用いてテストデータ期間の予測を行う
Args:
mcmc_samples (dict): MCMC のサンプル ({'pi', 'theta'})
z_samples (numpy array): 事後分布から取得したクラスタ割り当て (num_samples, n_series)
test_data (ndarray): テストデータ (n_series, test_time)
agent_models (list): エージェントモデルのリスト
Returns:
dict: 予測の平均・信頼区間 (n_series, test_time)
"""
num_samples, n_series = z_samples.shape # (num_samples, n_series)
_, n_agents = mcmc_samples["theta"].shape[1:] # (num_samples, n_clusters, n_agents)
test_time = test_data.shape[1]
# 各サンプルで予測値を計算
all_preds = []
for i in tqdm(range(num_samples)): # MCMC サンプルごとに計算
theta = mcmc_samples["theta"][i] # (n_clusters, n_agents)
z = z_samples[i] # (n_series,)
# 各系列ごとのエージェントモデルの予測
agent_preds = jnp.array([
[model(series, test_time) for model in agent_pred_models] for series in test_data
]) # (n_series, n_agents, test_time)
# 転置して形を揃える
agent_preds = agent_preds.transpose(0, 2, 1) # (n_series, test_time, n_agents)
print("agent_preds.shape:", agent_preds.shape) # デバッグ用
# クラスタ割り当てに基づき theta を取得
theta_z = theta[z] # (n_series, n_agents)
# Poisson 分布の平均パラメータ λ を計算
lambda_mean = jnp.exp(jnp.sum(theta_z[:, None, :] * agent_preds, axis=-1)) # (n_series, test_time)
lambda_mean = jnp.maximum(lambda_mean, 1e-5)
all_preds.append(lambda_mean)
all_preds = jnp.array(all_preds) # (num_samples, n_series, test_time)
# 予測の統計量を計算
summary = {
"mean": jnp.mean(all_preds, axis=0), # 平均
"ci_95": (jnp.percentile(all_preds, 2.5, axis=0), jnp.percentile(all_preds, 97.5, axis=0)) # 95% 信頼区間
}
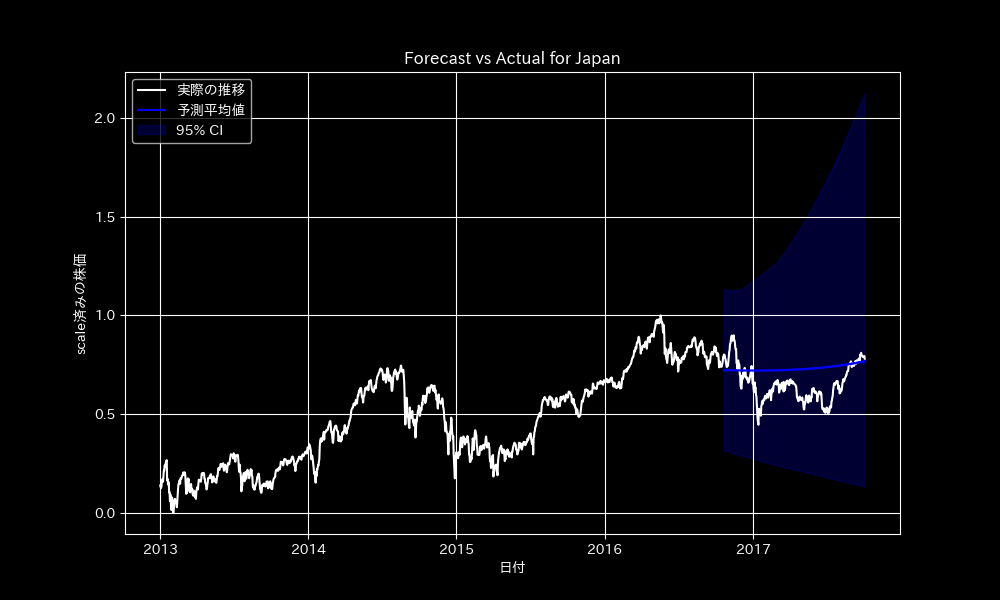
return summaryMBPSモデル
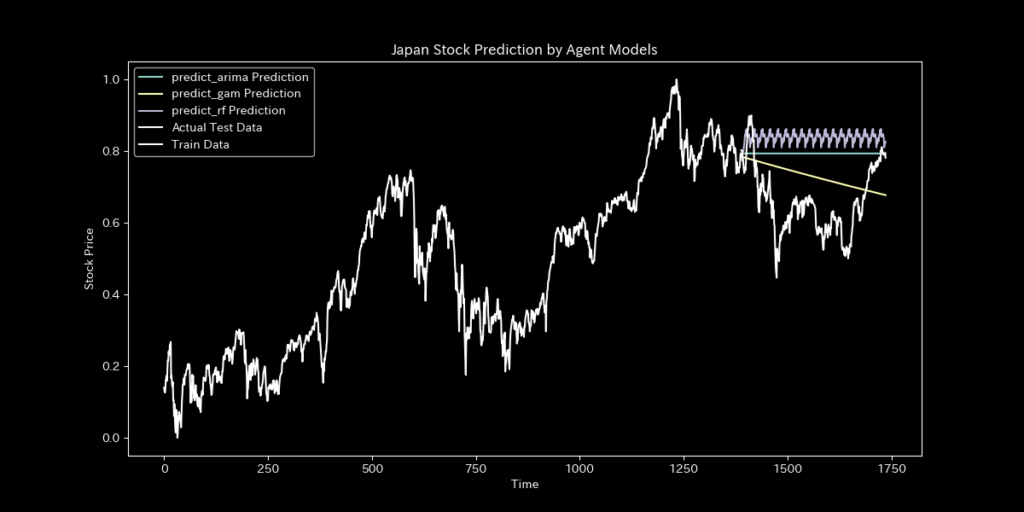
各エージェントモデル
指標
TOPIXの指標を比較いたします。
| MBPS | ARIMA | GAM | RandomForest | |
|---|---|---|---|---|
| MAE | 0.09886 | 0.144863 | 0.103954 | 0.184816 |
| RMSE | 0.117298 | 0.164768 | 0.117960 | 0.203723 |
| MAPE | 16.394247 | 24.095852 | 17.052247 | 30.478922 |
| R2 | -0.640935 | -2.237850 | -0.6595278 | -3.949830 |
MBPSは予測精度(累積絶対誤差)や不確実性(95%予測区間のカバレッジ)で他の手法(エージェントモデル)を上回りました。
4.おわりに
MBPSを使用するにあたり、特に重要なのはエージェントモデルとクラスタ数の選択です。特定のエージェントモデルが予測に失敗した場合、その影響がMBPS全体に及ぶリスクがあります。また、クラスタが多すぎるとパラメータ数が増加し、モデルが過度に複雑化してしまいます。逆に少なすぎると、異なる動態を持つ時系列が同じクラスタにまとめられ、予測精度が低下する可能性があります。
今回の実装では、チャートの終値という連続値データを使用しました。しかし、MBPSで用いられるポアソン回帰モデルはカウントデータを前提としているため、今後の応用ではカウントデータの使用を推奨します。論文でも述べられているように、MBPSはパンデミック対応や医療リソース計画において重要な役割を果たす可能性があります。
一方で、チャートデータはランダムウォーク要素が強く、政治や環境問題など他の要因が大きな影響を及ぼすため、単にエージェントモデルを組み合わせるだけでは十分な対応が難しい場合が多く見受けられました。その結果、分散が大きくなり、予測の信頼区間が広がるという課題も明らかになりました。