※サムネイルはOpenArt.aiより取得。

Index

はじめに
1. MLP vs KAN
2. 高校数学でKANの利点を理解する
おわりに
参考
オウンドメディアも運営しています

はじめに

　データソリューション事業部の関田です。

　2024年4月30日、arXivにてKAN: Kolmogorov-Arnold Networks (Liu Z, et al., 2024) という論文が発表されました。KANは従来の多層パーセプトロン (MLP) と比べていくつか利点を持っており、発表から数日でKANを応用した研究が続々と発表されるほど注目を浴びています。

　本記事では、初めにMLPとの違いに注目してKANの特徴および利点を挙げていきます。その後、高校レベルの数学に落とし込んでKANの利点について具体的に解説します。この単純化により厳密な説明が不十分になりますが、その分KANの核心を抽出して解説します。

1. MLP vs KAN

　まずはMLPとKANの違いおよびKANの利点について概要を説明します。図1.1は、元の論文に掲載されているMLPとKANの比較をまとめた図です。

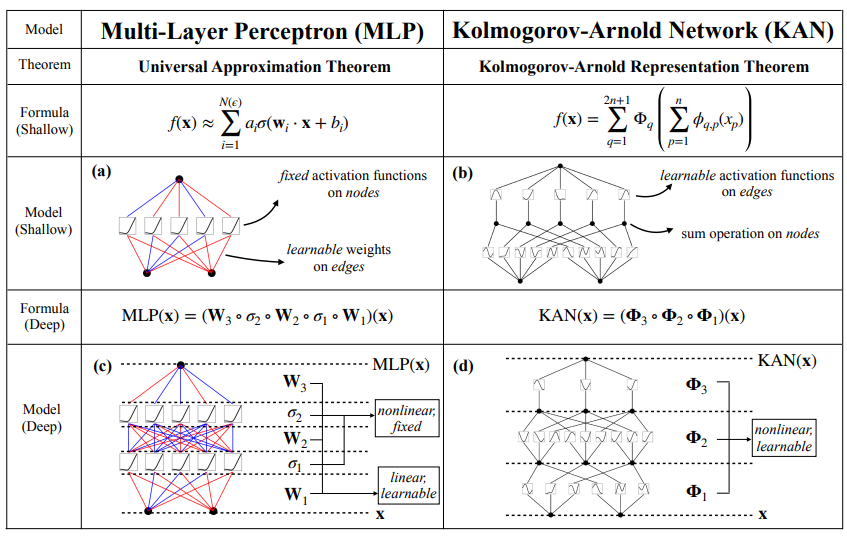
肝心な点は図1.1の”MODEL (Shallow)”, “MODEL (Deep)”の行です。該当行で述べている、MLPとKANの違いは以下の通りです（色付き太字部分については、2章で具体的に解説します）。

MLP

ノード：
接続される各エッジからの入力に対して、学習不可能であらかじめ決まった非線形変換を行う。その後、変換された全結果を足し合わせて次のエッジに結果を渡す。

エッジ：
各ノードからの入力に対して、学習可能なパラメータを持つ関数による線形変換を行い、次のノードに結果を渡す。

KAN

ノード：
接続される各エッジからの入力を足し合わせ、次のエッジに結果を渡す。

エッジ：
各ノードからの入力に対して、学習可能なパラメータを持つ関数による非線形変換を行い、次のノードに結果を渡す。

　ここで注目していただきたいのが「学習可能/学習不可能」、「非線形変換/線形変換」という言葉です。モデルの表現力や柔軟性という観点において、赤字が強み、青字が弱みを表します。
　MLPではそれぞれが入り混じっていましたが、KANでは強みだけを利用することで構造を単純化しています。これによって、現在深層学習の分野で課題に挙げられている、パラメータ数の増大を抑えることが期待されます。
　さらに、MLPに比べてモデルの解釈性が高いことも利点として挙げることができます。それぞれの変換はMLPに比べて複雑になりますが、その分KANの各変換の方が直接的に表現することができますし、変換の回数も少ないです。
　他にも利点はありますが、ここでは上記2点を代表的なKANの利点として挙げさせていただきます。
　公平のため、現在のKANの欠点についても触れておきます。KANは同じパラメータ数のMLPに比べて、モデルの訓練にかかる時間が長いです。したがって、モデルの訓練に時間をかけたくない場合はMLPを使うべきです。
　ただし、計算時間についてはまだ深く研究されていません。計算時間以外の面でKANが認められていけば、計算方法が最適化されていくことは想像に難くありません。

KANの利点・欠点まとめ

利点

パラメータ数を削減することができる
解釈性に優れる

欠点

計算時間が長い

　では、なぜ上に挙げた赤字が利点につながるのかについて考えていきましょう。

2. 高校数学でKANの利点を理解する

　KANが行っている「学習可能なパラメータを持つ関数による非線形変換」の強みについて解説します。

※MLPでは行列を用いて線形変換を行いKANではスプライン曲線を用いて非線形変換を行いますが、ここでは行列やスプライン曲線については触れないこととします。線形変換は一次関数による変換、非線形変換は二次関数、三次関数、、、による変換とし、あくまでモデルの表現力という観点でそれぞれの違いを解説します。

2.1. n次関数の表現力

　以下の一次関数で与えられる値 \(y\) は \(x\) を線形変換したものです。「線形」という由来は、図2.1の通り、変換する一次関数が直線であることです。

\[y = ax+b \quad (a \neq 0)\]

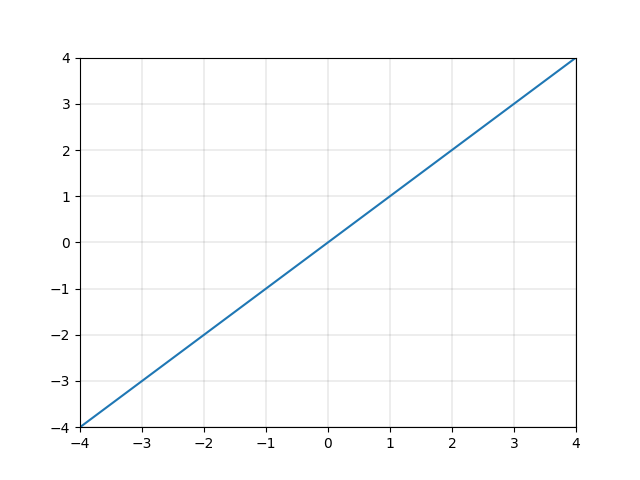
一方、図2.2や図2.3で表す二次関数や三次関数など、多くの関数は直線ではありません。これらをまとめて「非線形な関数」と呼び、これらの関数による変換を「非線形変換」と呼びます。

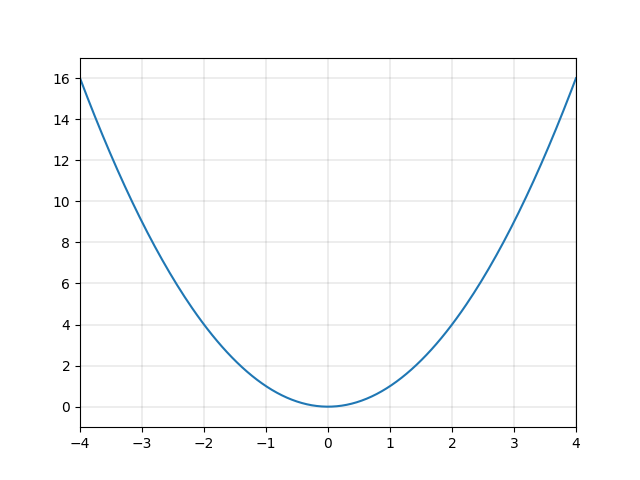
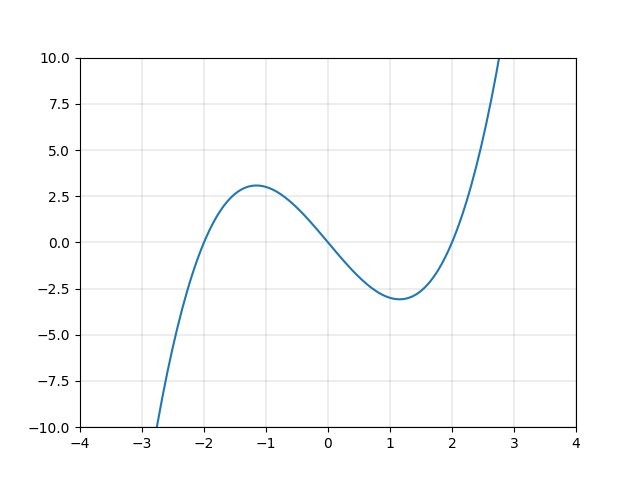
一次関数は、直線というシンプルな形状ゆえに、複雑な変換をするには向いていません。例えば一次関数を組み合わせて、図2.4のようななめらかで周期的な関数 \(y=\sin{x}\) を表現するのは大変でしょう。

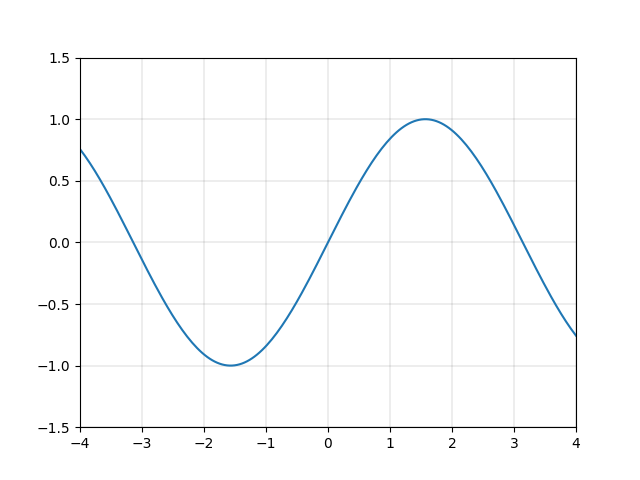
それに対し、二次以上の関数を使用することができれば、\(y=\sin{x}\) などの関数を精度良く近似的に表現することができます。例えば図2.5に示す関数 \(y=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}-\frac{x^{11}}{11!}\) は、図2.4の \(y=\sin{x}\) にそっくりです。

※近似的に表す方法については高校の上級レベルまたは大学レベルの数学が関係するので、これ以上の説明は省略します。気になる方は「テイラー展開」「マクローリン展開」などを勉強してみてください。

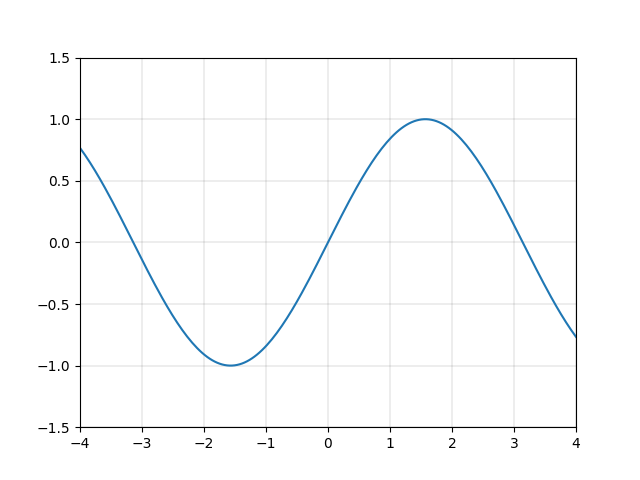
図2.5. \(y=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}-\frac{x^{11}}{11!}\) のグラフ

このように、 \(x\)のべき乗から成る非線形関数を用いて様々な曲線を描くことができるのです。非線形変換の強みをイメージしていただけたでしょうか。

2.2. MLPの変換方法

　1章にて述べたように、MLPの変換は以下の2種類です。

学習不可能であらかじめ決まった非線形変換
学習可能なパラメータを持つ関数による線形変換

この通りMLPでも非線形変換は行われますが、MLPの非線形変換は学習不可能なのでデータに合わせた変換を行うことはできません。その代わりMLPではモデルにフィットする線形変換を学習するのですが、直線的な変換しかできないため、複雑なデータにフィットさせるには多くの変換を組み合わせる必要があります。

2.3. KANの変換方法

　KANでは、学習可能なパラメータを持つ関数による非線形変換を行います。2.1節で述べたように、\(x\) のべき乗から成る多項式でも色々な関数を表現することができるので、MLPに比べて複雑なデータにフィットさせることが容易になります。

　図2.6は、3層のKANが \(y=\exp{(\sin(x_1^2+x_2^2)+\sin(x_3^2+x_4^2))}\)という一見複雑な関数を学習していく様子を表しています。 \(x_1, x_2, x_3, x_4\) という4つの入力に対して、

1層目のエッジで入力の2乗を計算し、
直後のノードでそれらの和を取り次への入力とし、
2層目のエッジで入力を引数とする \(\sin\) の値を計算し、
直後のノードでそれらの和を取り次の入力とし、
3層目のエッジで入力を引数とする \(\exp\) の値を計算して、

最後に結果を出力しています。

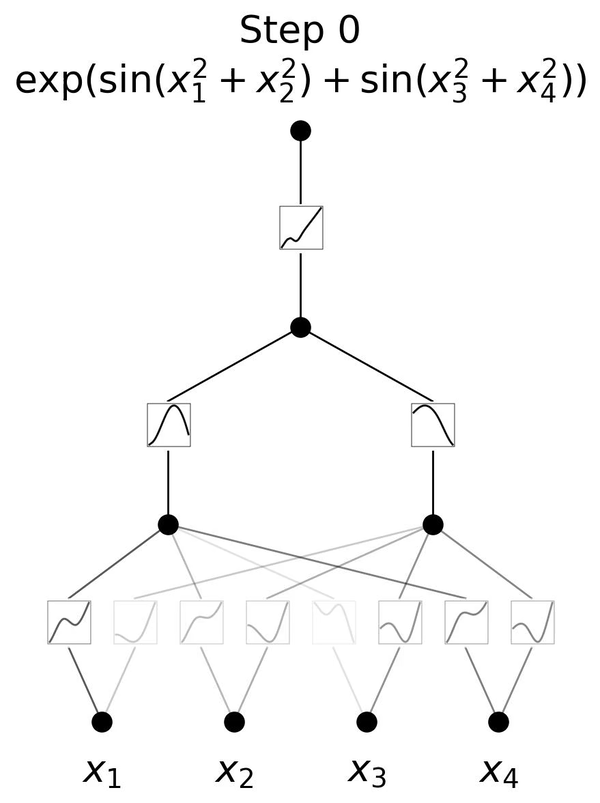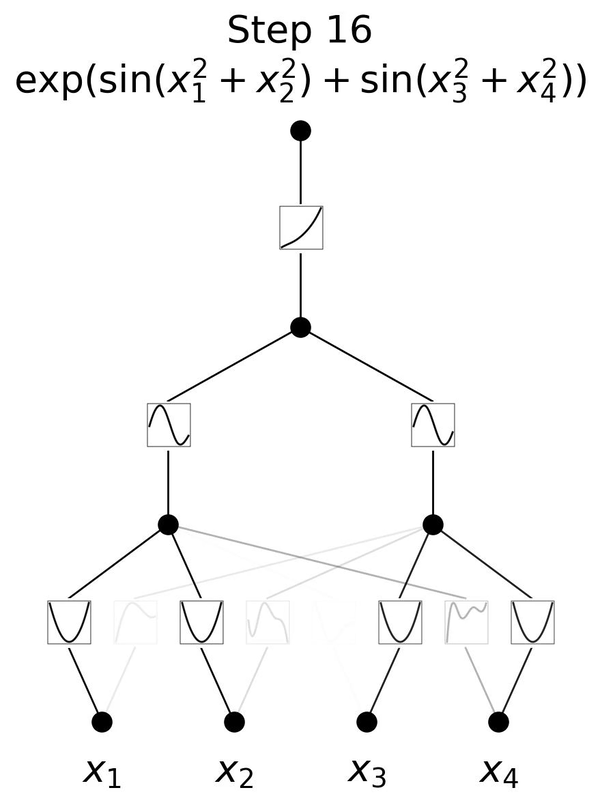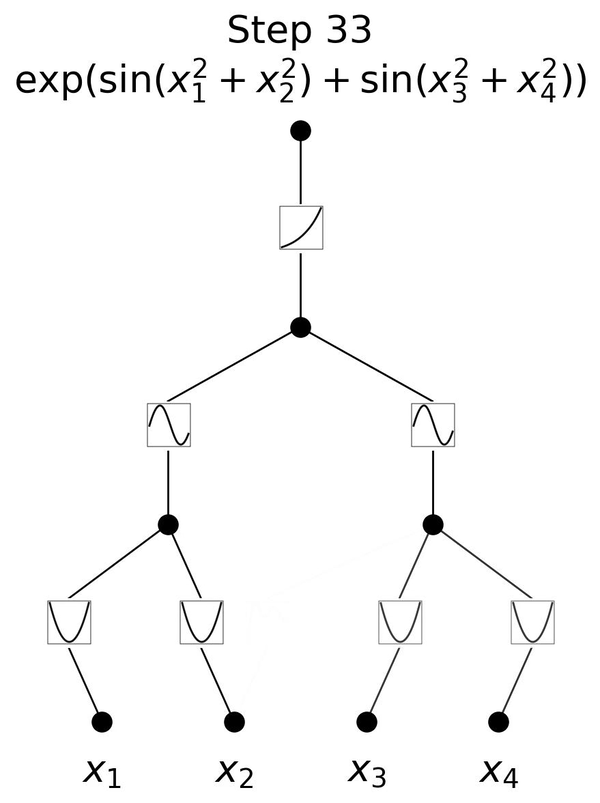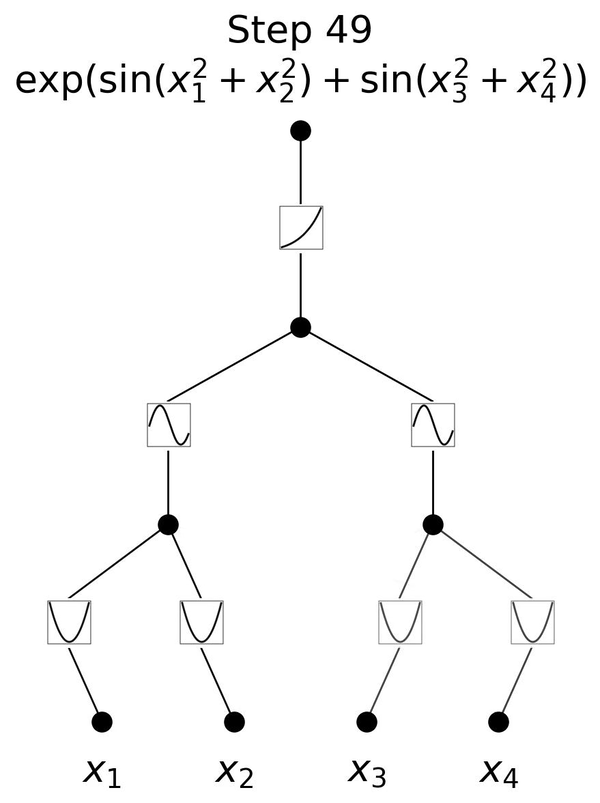
図2.6. KANが関数 \(y=\exp{(\sin(x_1^2+x_2^2)+\sin(x_3^2+x_4^2))}\) にフィットするよう学習する様子 (出典: pykan (Liu Z, et al., GitHub, 2024)

この流れは、人間が \(y=\exp{(\sin(x_1^2+x_2^2)+\sin(x_3^2+x_4^2))}\) を理解する手順と同じです。各エッジが2乗、 \(\sin\)、 \(\exp\) をそのまま表すことができるKANだからこそ、図2.6のように分かりやすく可視化できているのです。

　最後に繰り返しますが、KANがこれらのことをできる理由は、学習可能なパラメータを持つ関数による非線形変換を行っているからです。本記事がこのキーワードの理解の助けになれば幸いです。

おわりに

　今回は、一部のタスクでMLPを凌駕したKANという新たなAI技術の利点について解説しました。本記事で高校数学にまで落とし込んで解説することが可能であった理由は、KANが「難解な技術を駆使して創り上げられた」のではなく「基本的な発想を組み合わせ、それを実現させた物」であるからだと個人的には思っています。

　KANはMLPに並ぶ基礎的な技術であるため、その土台としての強固さが認められれば、今後様々な方向へ発展し、応用され、世界を支える技術となることでしょう。その可能性を秘めた技術の誕生に立ち会えたことに興奮を覚えながら、本記事を締めさせていただきます。

参考

[1] Ziming Liu, Yixuan Wang, Sachin Vaidya, Fabian Ruehle, James Halverson, Marin Soljačić, Thomas Y. Hou, Max Tegmark. KAN: Kolmogorov-Arnold Networks. arXiv preprint arXiv:2404.19756v2, 2024.

[2] Ziming Liu, et al. pykan. GitHub, 2024.

オウンドメディアも運営しています

この記事がよかったら
シェアしてください。

KAN (Kolmogorov-Arnold Networks) の利点を単純化して理解する