Index
- はじめに
- モデルマージとは
- モデルマージの手法
- Editing Models with Task Arithmetic (2022-12-08)
- TIES-Merging- Resolving Interference When Merging Models (2023-06-02)
- Language Models are Super Mario- Absorbing Abilities from Homologous Models as a Free Lunch (2023-11-06)
- Model Breadcrumbs: Scaling Multi-Task Model Merging with Sparse Masks (2023-12-11)
- Localizing Task Information for Improved Model Merging and Compression (2024-05-13)
- DELLA-Merging: Reducing Interference in Model Merging through Magnitude-Based Sampling (2024-06-17)
- MetaGPT: Merging Large Language Models Using Model Exclusive Task Arithmetic (2024-06-17)
- Model merging with SVD to tie the Knots (2024-10-25)
- その他:モデルマージに関連するトピック
- モデルマージの実装方法
- おわりに
- 参考文献
- その他 参考資料
- オウンドメディアも運営しています
はじめに
データソリューション事業部の宮澤です。今回はLLMのモデルマージ技術について解説します。モデルマージとは、複数のモデルのパラメータを何かしらの形で合成することによって新たなモデルを構築する技術のことを指します。この手法を活用することで、事前学習やファインチューニングのように、複雑で計算量の大きい処理を伴うことなく、高性能なモデルを効率的に構築することが可能になると言われています。
本記事を執筆したきっかけは、NeurIPS 2024併設の LLM Merging Competition というコンペに参加したことです。このコンペでは、LLMをモデルマージすることによって汎用性能の高いモデルを作ることをゴールとしていました。本コンペの活動の一つとしてLLMのモデルマージ手法の調査を行いましたので、本記事ではそのまとめを公開します。
また、本記事では、ここにまだ記載できていない手法や新たに提案された手法を随時追加していくことを予定しています。
モデルマージとは
モデルマージとはその名の通り、複数のモデルを一つに統合することを指します。LLMにおいては、特定の下流タスク向けに微調整されたモデルを単一のモデルにまとめることで、様々なタスクを解くことができる汎用性の高いモデルを構築できる可能性があります。また、一般的なモデルマージの手法は勾配法を使うような訓練を不要としているため、計算コストが少ないという利点があります。
モデルマージの種別
モデルマージに関する技術を体系的に整理した論文 Model Merging in LLMs, MLLMs, and Beyond: Methods, Theories, Applications and Opportunities [1] では、モデルマージの手法を2つのステップに分解しています。1つ目は Pre-Merging Method とされており、効果的にモデルマージをするための前処理や学習の手法のことを指しています。2つ目は During Merging Method とされており、実際のモデルマージの処理のことを指します。本記事では、During Merging Method について取り扱います。
マージ対象による分類
モデルマージには様々な考え方や手法が存在しますが、本記事ではEvolutionary Optimization of Model Merging Recipes [2] で整理されているマージの種類を引用します。
1, パラメータ空間でのマージ
1つ目がパラメータ空間でのマージです。これは同じアーキテクチャを持つモデル同士で各レイヤーのパラメータの重みを統合する方法です。
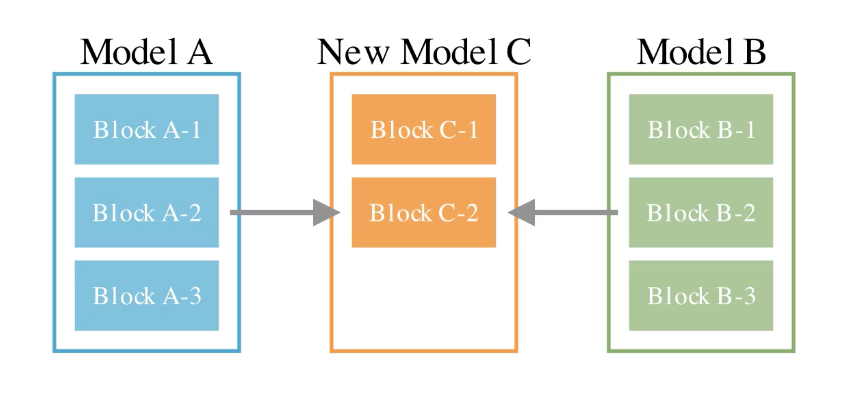
2, データフロー空間でのマージ
2つ目がデータフロー空間でのマージです。これは複数のモデルのレイヤーを選択して並び替えることで単一のモデルを作る方法です。
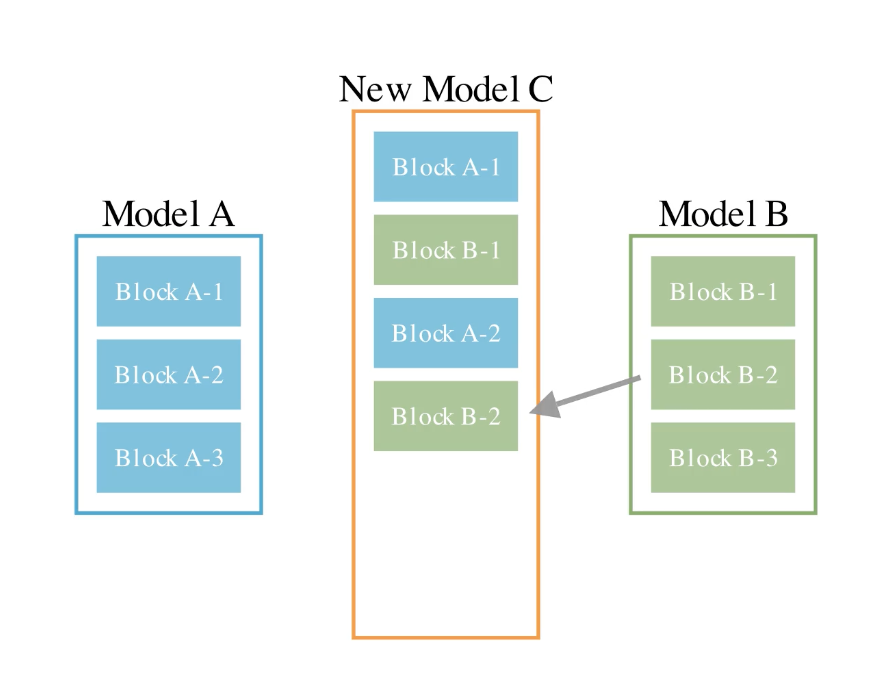
3, パラメータ空間とデータフロー空間の両方でのマージ
3つ目はその両者を使ったマージです。パラメータ空間のマージとデータフロー空間のマージの両方を組み合わせることで、さらに高度なマージを行うことができるとされています。
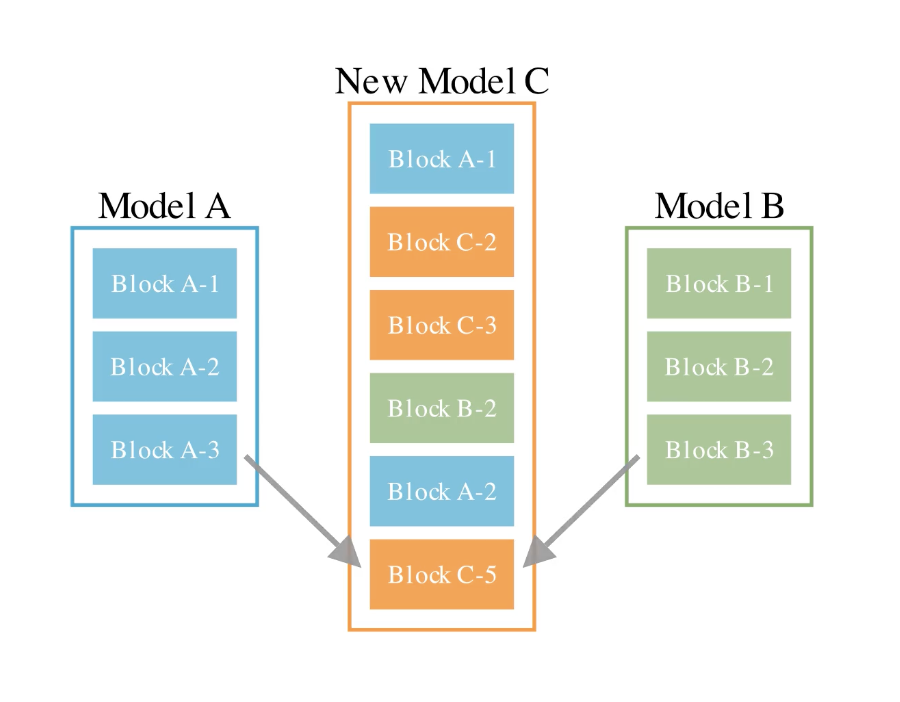
LLM Merging Competition においては、評価時のスクリプトがHuggingFaceのtransformersを使う実装となっていました。本ライブラリにクラスとして登録されていないアーキテクチャを実装することは実装難易度と工数が大きいと判断したため、既存のアーキテクチャに存在しないモデルを作るデータフロー空間のマージは避けました。したがって、パラメータ空間のマージに焦点を当て、モデル同士の重みをどのように統合するかという点で考えていました。これを踏まえて本記事においても「パラメータ空間でのマージ」に焦点を当てて解説するものとします。
モデルマージの効果
具体的なモデルマージの手法を説明する前に、モデルマージ自体の有効性について確認しておきます。パラメータ空間でのマージの有効性を示した論文で代表的なものとしては、Model soups: averaging weights of multiple fine-tuned models improves accuracy without increasing inference time [3] が挙げられます。
本論文では、大規模な事前学習済モデルに対して異なるハイパーパラメータで微調整された複数のモデルの重みを平均化することで、推論コストやメモリを追加することなく精度とロバスト性を向上させたことが報告されています。このモデルの平均化を「モデルスープ」と呼びます。
以下は本論文で報告されている、CLIP ViT-B/32での実験結果です。横軸はImageNetの分類精度で、縦軸はその他の5つの分布外タスク(ImageNetとは異なるタスク)の精度です。図4の緑の菱形は異なるハイパーパラメータで微調整したモデルであり、青い丸はそれら全ての重みを一様に平均化した場合のモデルです。右上の紫の星は、モデルスープに順次モデルを追加していき、スコアが下がらない場合のみモデルを平均するという形で貪欲なマージを行ったモデルとなっています。これを見ると、平均化されたモデルが多くの単体モデルよりも高い精度となっており、また高いロバスト性を獲得していることがわかります。
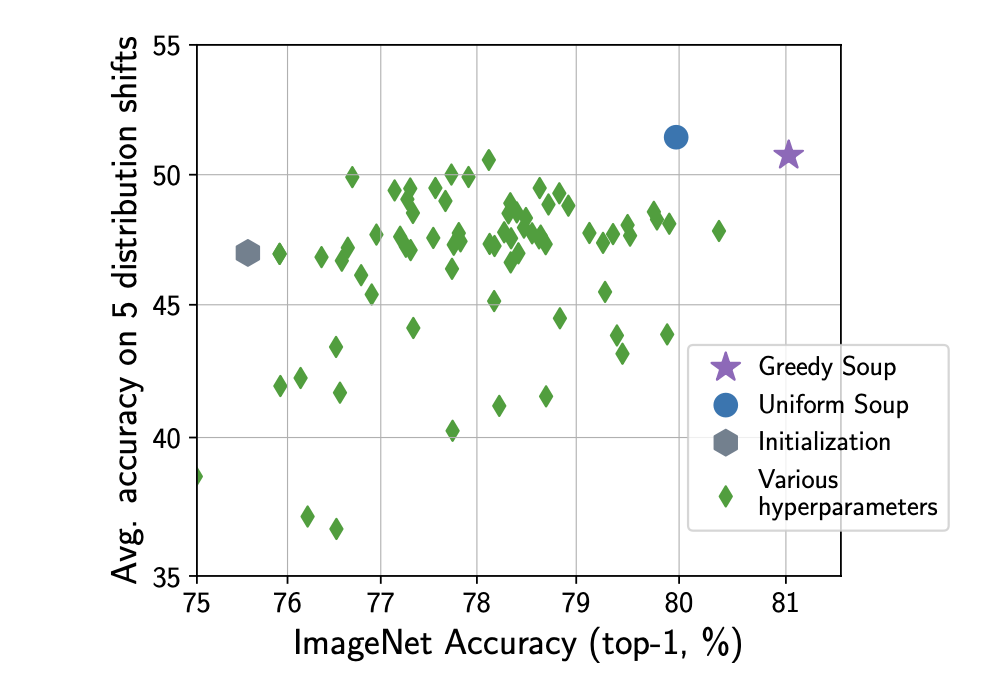
自然言語処理タスクに対する適用性についてはさらなる調査が必要であると述べられていますが、以下の実験結果からはモデルスープが有効である可能性が見受けられます。

また、本論文では、なぜこのように重み平均によるマージが効果的であるかを実験を通して分析しています。
以下の図5はその実験結果の一つです。横軸と縦軸が微調整時のパラメータの変動であり、初期地点から矢印の方向へパラメータが微調整されたことを示しています。色はこのパラメータ空間における損失地形を表しています。この図から、損失が最小となる最適解は微調整されたパラメータの位置ではなく、微調整されたモデル同士の間に位置していることがわかります。この結果から、個々のモデルよりも重みを平均化したモデルの方がより優れている可能性があることが示されています。
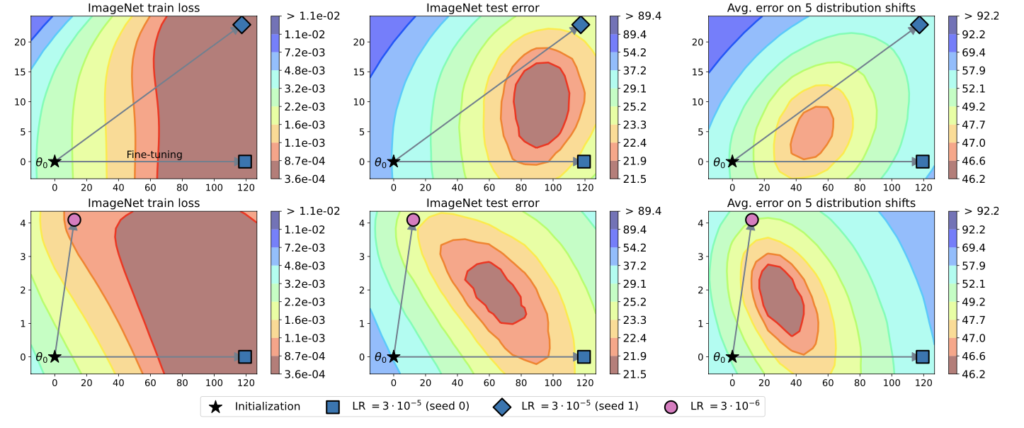
次に、図6はモデルスープとアンサンブルとの比較結果を示した図になります。横軸は図5で示しているパラメータ空間におけるモデル同士の矢印のなす角の大きさであり、縦軸はアンサンブルした場合の正解率との差分です。したがってこの図では、モデルスープによるタスク正解率がアンサンブルの場合よりも高くなる傾向があることが示されています。
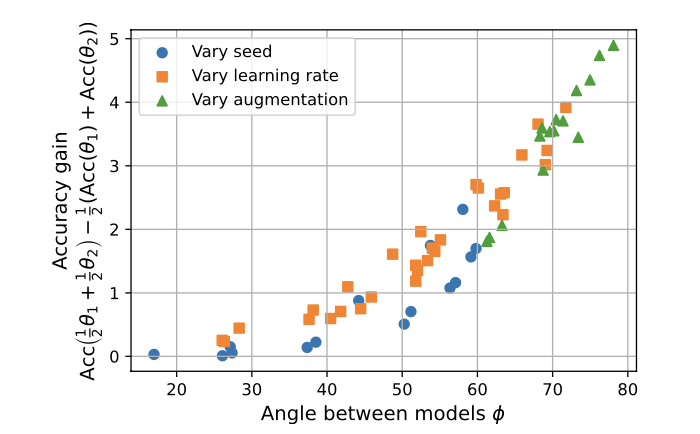
さらに、図7はモデルスープとアンサンブルとの性能差を、学習率の違いおよびタスクの違いによって検証した結果です。横軸はモデルスープによる正解率、縦軸はアンサンブルによる正解率で、色は学習率を示しています。また、左図はImageNetのタスクに対する評価であり、右はそのほかの分布外タスクに対する評価です。左図からはImageNetではアンサンブルでの性能が高く、右図からは分布外タスクにおいてはモデルスープの性能がやや高いことがわかります。
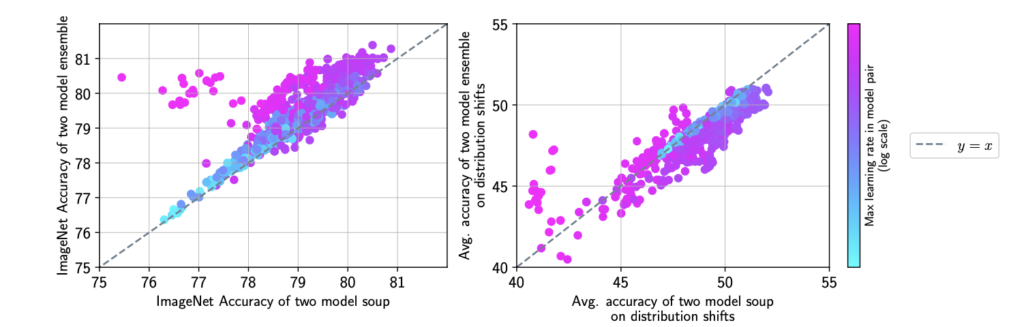
以上のように、平均化によるモデルマージ(モデルスープ)では、個々の微調整モデルよりも汎用的な精度の高いモデルとなる可能性があり、単純なアンサンブルと比較すると特に分布外タスクへの性能が高いことから、高いロバスト性を獲得できていることが報告されています。これはニューラルネットワークの損失地形 (佐藤 2024)で述べられているように、重みを平均化することによって損失関数の「平坦解」に近づいているためであると解釈することもできます。
モデルマージの手法
モデルスープは最も基本的な単純平均によるマージでした。ここからは他のモデルマージの手法を深掘りしていきます。なお、本記事の第1版としては、mergekitというライブラリで実装されている手法を中心にまとめています。(随時更新する予定です。)
以下、論文タイトルの括弧にはarXivでの公開日を記載しています。
Editing Models with Task Arithmetic (2022-12-08)
まず初めに、Editing Models with Task Arithmetic [4]について紹介します。本論文は、最近のモデルマージ手法において多く用いられている「タスクベクトル」という概念を提唱したものです。
タスクベクトルとは、微調整したモデルのパラメータの重みから微調整前のパラメータの重みを引くことによって得られる、「そのタスクを解く機能を持ったパラメータとその重み」を意味します。事前学習済みのパラメータを\(\theta_{\text{pre}} \in \mathbb{R}^d\)として、タスク\(t\)に対する微調整後のパラメータを\(\theta_{\text{ft}}^t \in \mathbb{R}^d\)とすると、タスクベクトルは \(\tau^t = \theta_{\text{ft}}^t – \theta_{\text{pre}}\)と表すことができます。
本論文では、タスクベクトルは以下のように加減算して扱うことができると述べられています。
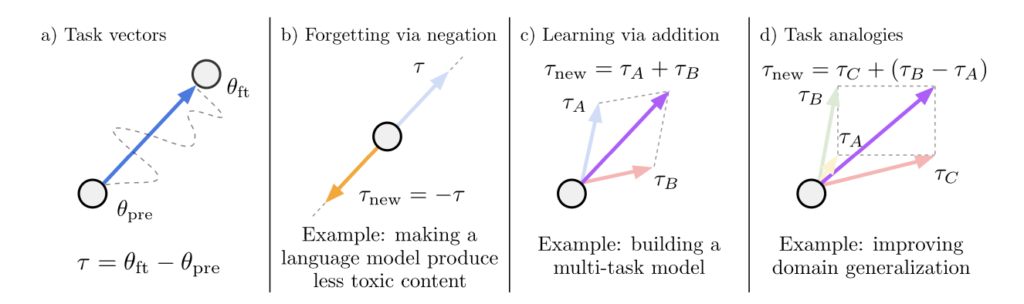
例えば、 図8 b)ではタスクベクトルを減算することによってそのタスクの能力を忘却させられること、c)では2つのタスクベクトルを加算することによってマルチタスクの能力が獲得できることが図示されています。さらにd)では、教師データの存在するドメインで学習したタスクベクトルを用いた加減算によって、教師データのない別のドメインでの同類タスクを解く能力を獲得することができることを示しています。b)の加算・c)の減算に対するイメージは比較的掴みやすいと考えられるため、ここではd)のTask analogiesについて詳細を説明していきます。
本論文ではYelpというデータセットに対する感情分類の機能を獲得する実験を行っています。実験設定としてはYelpに対する教師データは所持しておらず、別のドメインであるAmazonのレビューのデータセットにおける感情分類の教師データは所持しているものとしています。
ここで、Yelpに対する感情分析のタスクベクトルを獲得するためのTask analogiesは以下の式で組み立てることができます。
$$ \hat{\tau}_{\text{yelp;sent}} = \tau_{\text{amazon;sent}} + (\tau_{\text{yelp;lm}} – \tau_{\text{amazon;lm}}) $$
\(\tau_{\text{yelp;lm}}\)と\(\tau_{\text{amazon;lm}}\)は、両データセットの入力に対する教師なし言語モデリングによって得られた重みであると述べられています。これらのタスクベクトルは、自己教師あり学習(次トークン予測による事前学習)によって獲得されたものであり、ドメインの知識を内包すると仮定されたベクトルであると考えられます。このことを踏まえて全体の式を解釈すると、Yelpの感情分析のタスクベクトル = Amazonの感情分析のタスクベクトル + (Yelpドメインモデル – Amazonドメインモデル) と読み取ることができます。この加減算によって、Yelpにおける感情分析の教師データがない場合でも、他のドメインで得られた重みを再利用することで、擬似的にタスクベクトルを獲得することができると述べられています。
本論文ではこのように、ファインチューニングモデルから事前学習済みモデルの重みを引くことでタスクベクトルを獲得し、その加減算によってタスク能力を付与できることが述べられています。この「タスクベクトル」は後続の研究でも活用されている重要な概念となっています。
💡SLERP (Spherical Linear Interpolation)によるマージ
本記事で述べている手法は基本的にパラメータの重みをベクトルとして線形補間するものですが、これを球面線形補間でマージする方法もあります。これはベクトル同士の直線的な経路ではなく、ベクトル同士の角度を考慮して球面上の大円に沿うように補間をする方法です。これによってパラメータの非線形な特性を保持することができると考えられています。
参考:https://gist.github.com/dvschultz/3af50c40df002da3b751efab1daddf2c
TIES-Merging- Resolving Interference When Merging Models (2023-06-02)
ここでは、TIES-Merging- Resolving Interference When Merging Models [5]で提案されているTIESというマージ手法を紹介します。
本手法のポイントは2つあります。
- デルタパラメータの枝刈り
- 優位な符号に一致する重みのマージ
上記の2つのステップは、本記事で後述するマージ手法でも共通した考え方があります。なお、ここで述べている「デルタパラメータ」は、[4]で使われていた「タスクベクトル」と同義の概念です。論文によって使われる言葉が異なるため、本記事では各論文の表記に合わせます。
前提として、TIESを含む多くのモデルマージに関する論文で課題として述べられているのが、パラメータ干渉です。パラメータ干渉とは、マージする際にそれぞれのモデルのパラメータの重みがお互いに悪く影響し合うことで、結果的に性能が劣化するように統合されてしまう現象のことを指します。
本論文ではパラメータ干渉を2つの観点から見ています。
- 1つ目は「冗長なパラメータの干渉」です。微調整後のデルタパラメータの中には、実際にはほとんど影響を与えない冗長なパラメータが存在し、それがマージの際に他のモデルの影響力のある重みに干渉することでパラメータの影響が埋もれてしまい、性能劣化につながると考えられています。
- 2つ目は「符号の不一致による干渉」です。モデル間で逆向きの符号を持つデルタパラメータの重みを単純にマージすることで、お互いのタスク性能を打ち消し合うように影響してしまうと考えられています。
TIESでは、1つ目の冗長なパラメータの干渉を解消するために「枝刈り」を、2つ目の符号の不一致による干渉を解消するために「優位な符号との一致によるマージ」を行っています。他のマージ手法についても、枝刈りの方法かマージそのものの算術のどちらかで差別化されることが多いため、この2つの観点で見ていくことで手法の違いを理解しやすくなります。
TIESでは以下のような流れでマージが行われます。
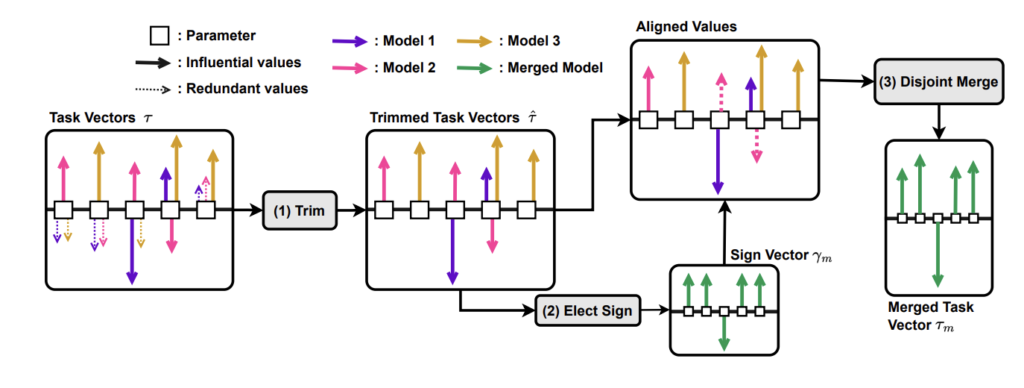
まず初めに各モデルのデルタパラメータを算出します。これは上述した通り、元のモデルと微調整後のモデルの重みの差分です。
次に枝刈りです。図9の左の図で点線で示されているように、TIESではデルタパラメータの絶対値が小さいものを削除します。ここでいう削除とは、デルタパラメータの重みを0にすることであり、言い換えると事前学習時点の重みに戻すことを意味します。これが冗長なパラメータの干渉への対応です。実験では上位約20%のデルタパラメータが残っていれば削除前と同等程度の精度を示すことが報告されています。
次に優位な符号に一致する重みをマージします。まずは枝刈り後のデルタパラメータを合計し、合計値の正負の符号を「優位な符号」として抽出します。(図9の(2) Elect Signの部分が該当。)その後、その符号の向きと一致するデルタパラメータのみを残して枝刈りします。(図9のAligned Valuesの部分が該当。)次に、残ったデルタパラメータのみを最終的に平均することによって統合します。最後に、統合された重みをベースモデルの重みに加算することで最終的なモデルの重みとします。これが符号の不一致によるパラメータの干渉への対応です。
なお、最後のステップでベースモデルに加算する際には、\(λ\)でスケーリングすることも提案されています。事前学習時の重みを残しつつマージを行うため、過学習を防ぐ効果があると考えられています。
本論文の実験結果は以下のように報告されています。
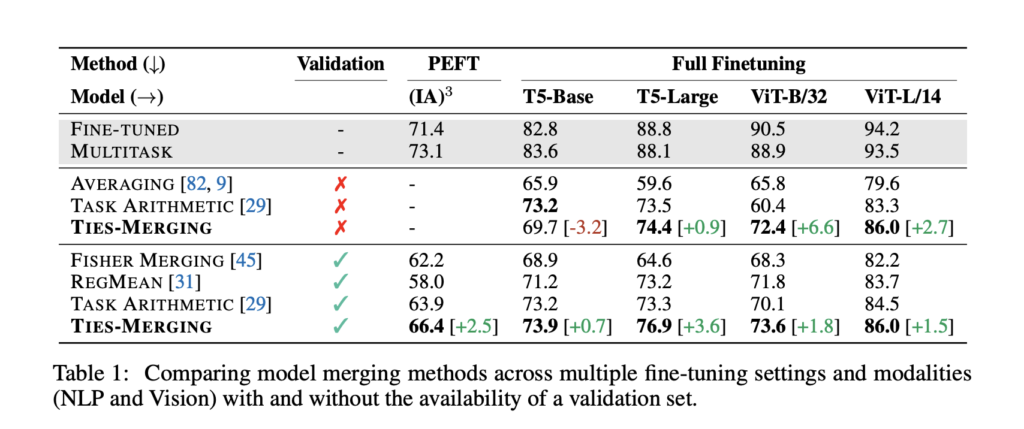
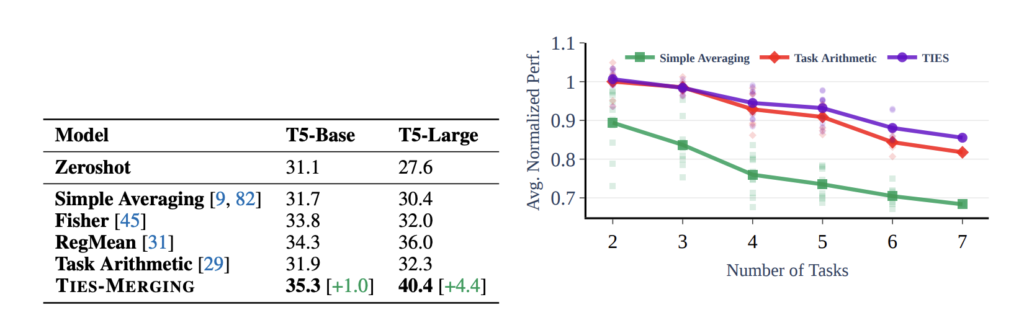
図10: TIES-Merging- Resolving Interference When Merging Models Figure 5より引用
表2では、交通標識分類などの画像タスクと質問応答などの言語タスクにおいて、T5-Baseモデルを使った場合を除いて、TIESが既存手法よりも高いスコアであったことが報告されています。また、表3では未知のNLPタスクに対する精度が高いこと、図10では単純な平均化によるマージと比べてタスク数(デルタパラメータの数)が増えたときの性能劣化が少ないことが示されています。これは単純な平均と比べてTIESが頑健な手法であることが示唆されています。(Simple AverageとTask Arithmeticの違いは、前者はフルパラメータの単純平均、後者の場合はタスクごとにデルタパラメータをスケーリングして加重平均しているものだと思われます。)
Language Models are Super Mario- Absorbing Abilities from Homologous Models as a Free Lunch (2023-11-06)
ここでは、Language Models are Super Mario- Absorbing Abilities from Homologous Models as a Free Lunch [6]で提案されているDAREという手法を紹介します。
DAREはDrops And REscalesの略であり、デルタパラメータの枝刈り部分の手法となっています。この手法はデルタパラメータをランダムに\(p\)の割合で枝刈りした後、残りのパラメータを\(1 / (1-p)\)でリスケーリングするというシンプルなものです。
提案手法の背景として、本論文では微調整済みのモデルのデルタパラメータには冗長な特性があることを主張しています。以下がその裏付けとなる実験結果です。

図11は、GSM8K(算数タスク)とHumanEval(コーディングタスク)の2つにおいて、DAREを使ったデルタパラメータの削除割合と精度の関係性を示しています。この結果から、約90%のデルタパラメータを削除(微調整前の重みに戻す)しても精度は大きく変わらず、特にパラメータサイズの大きなモデルであるほど削除に対して頑健であることが述べられています。
次に、リスケーリングに関する予備実験を見ていきます。同じように2つのタスク(GSM8K, CoLA)で実験がされています。
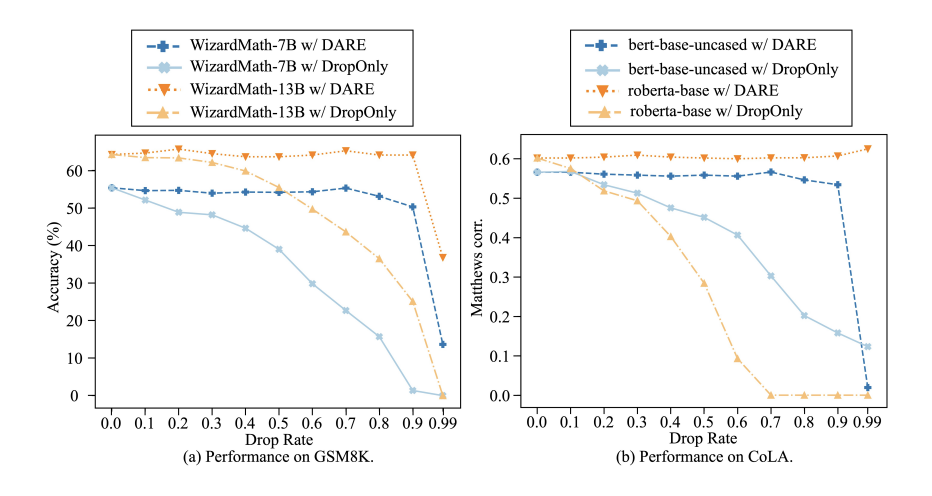
図12を見ると、リスケーリングをせずにデルタパラメータの削除のみを行うと、削除する割合が大きくなるにつれて精度が劣化していく一方で、リスケーリングを含むDAREでは約90%の削除まで大きく精度が変わらないことがわかります。この結果から、単純なデルタパラメータの削除だけではなく、リスケーリングが有効であることが明らかになりました。(数学的な裏付けについては本論文に記載があるため、そちらをご参照ください。)
ここで押さえておきたいのが、DAREは枝刈り段階の手法であるため、これとTIESなどマージの手法を組み合わせることが可能であるという点です。例えばDAREとTIESを組み合わせて使う場合、初めにDAREでランダムな枝刈りとリスケーリングを行い、その後TIESによる符号一致以降のマージ処理を行う形になります。
DAREの使用有無による精度の比較実験の結果が以下です。
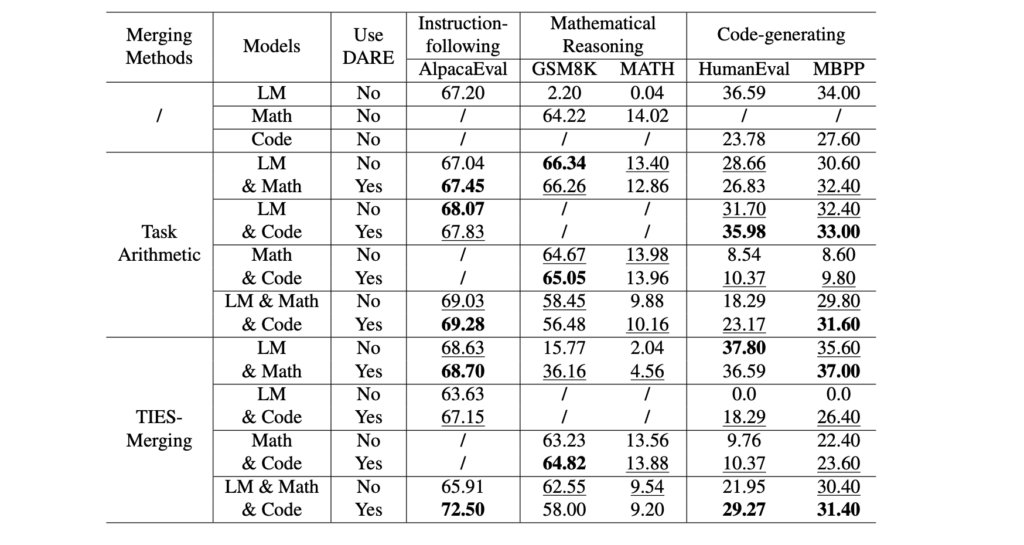
表4から、DAREを使うことで、使わない場合よりもしばしば良い結果が得られていることがわかります。ただし、必ずしも改善されるわけではないため、タスクやハイパーパラメータの設定によって異なる可能性があると考えられます。
また、DAREとの組み合わせではTask Arithmeticと比べてTIESでの改善がより多く見られると述べられています。TIESの枝刈りでは絶対値が小さいものを規則的に削除しますが、これが特定のモデルにとって重要なパラメータを落としている可能性があり、DAREではランダム性によりそのリスクが軽減されていると考えられるようです。
Model Breadcrumbs: Scaling Multi-Task Model Merging with Sparse Masks (2023-12-11)
ここでは、Model Breadcrumbs: Scaling Multi-Task Model Merging with Sparse Masks [7]で提案されているModel Breadcrumbsという手法を紹介します。
これはDAREと同じく主に枝刈り部分の処理における提案手法です。したがって、DAREと同じように枝刈り後のパラメータのマージは平均値を取ることもTIESのような符号一致を考慮した手法を組み合わせることも可能です。
本論文の問題提起としては2点あり、1つ目はモデルのパラメータにはアクセスできても学習に使われたデータがオープンでないため、同じようにモデルを作ることが困難であることです。2つ目はモデルマージではタスク数(モデル数)の増加に伴ってノイズが大きくなること(これまで述べてきたパラメータ干渉と同じような意味だと思われる)が挙げられています。1つ目はモデルマージを使うことが有意義であることを示しており、2つ目は提案手法の背景として述べられていると思われます。
Model Breadcrumbsの具体的な中身を見ていきます。
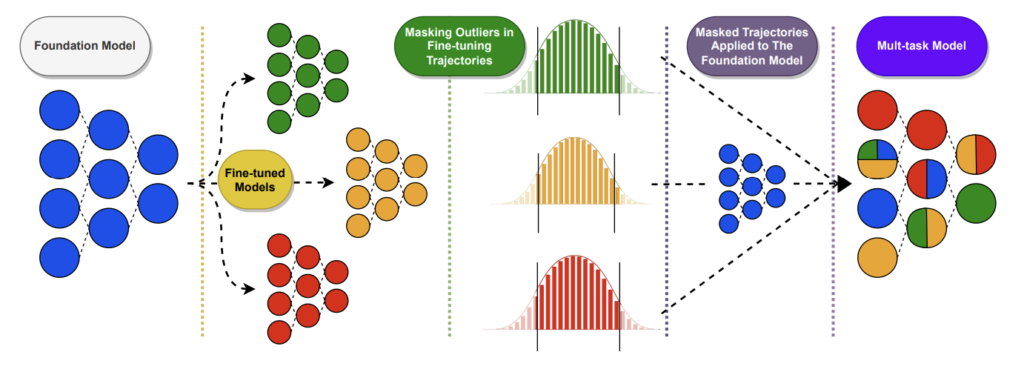
図13の通り手法はシンプルな枝刈りとなっています。デルタパラメータを算出する処理は先に紹介した手法と同じす。本手法は枝刈り部分に特徴があり、デルタパラメータの絶対値の上下を枝刈りします。これは外れ値を除去するイメージです。本論文では分布の左側の閾値を\(β\)、右側の閾値を\(γ\)と置いており、デルタパラメータを0に戻すかどうかを「マスク」と表現して\(m^{β, γ}_t\)と表しています。
マスクを適用して残ったデルタパラメータ同士の総和をとった後は、スケーリングのハイパーパラメータである\(α\)をかけてからベースモデルの重みと足し合わせる形となっています。
$$ \theta^* = \theta + \alpha \sum_{t \in T} m^{β, γ}_t .\theta^d_t $$
ハイパーパラメータについて、\(\beta, \gamma\)は\(\{\beta = 90\%, \gamma = 99\%\}, \{\beta = 90\%, \gamma = 99.2\%\}, \{\beta = 85\%, \gamma = 99\%\}\)の設定が最適であったと報告されています。つまり、実際に残るのは全体の約10~15%のデルタパラメータのみです。
ここでハイパーパラメータの設定についての補足ですが、本論文では\(\alpha\)と\(\beta\)の関係性、\(\beta\)と\(\gamma\)の関係性についての実験と考察がされています。以下の図14ではそれぞれのハイパーパラメータの値を軸に取り、データポイントの色の濃さで精度を示しています。
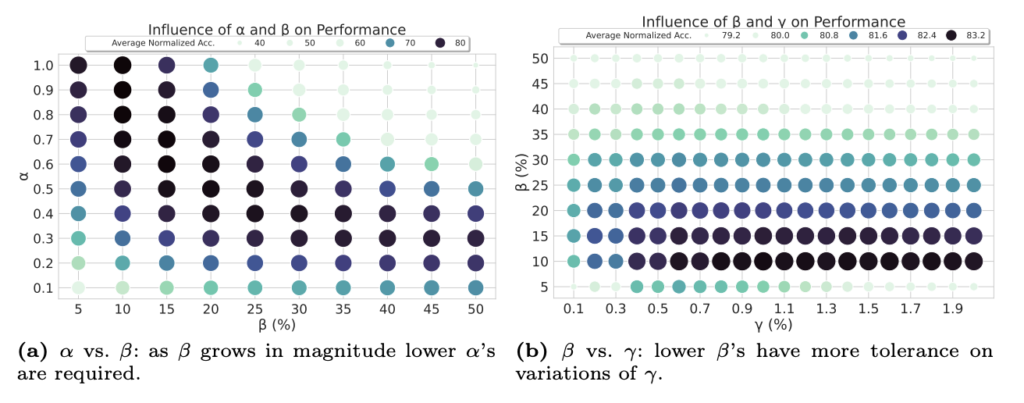
この実験結果をまず\(\alpha\)と\(\beta\)の関係性である左図から読み解くと、\(\beta\)を大きくする場合は\(\alpha\)は低く設定することで高い精度が保たれる傾向にあることがわかります。また、\(\beta\)と\(\gamma\)の関係性を示す右図については、\(\beta\)が低い場合は\(\gamma\)が高い方がよく、その逆も同様であることが示唆されています。
また、\(\beta\)および\(\gamma\)はどちらかを無効として、分布の上または下だけをマスクする形とした場合、両方をマスクする本手法よりも劣ることが実験から明らかになりました。 以下の図15が実験結果であり、両側からマスクする本手法(Model Breadcrumbs)は、上だけを切ったり下だけを切ったりするマスク方法と比較して精度が高く、かつ各タスクの精度のばらつきが少ないが少なかったことが報告されています。
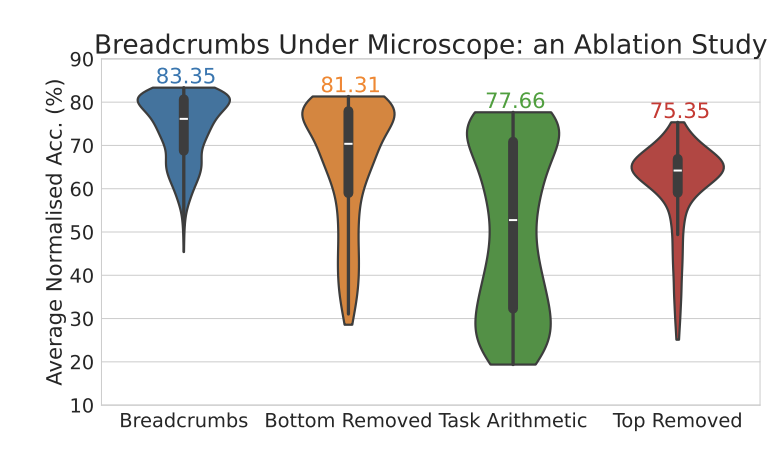
本手法を適用した場合の精度実験はいくつか行われているため一部を抜粋します。
表5はViT-B-32を使って8つのタスクで評価をした結果です。枝刈りをしないTask Arithmeticと比較すると、約6ポイント高いスコアとなったことが報告されています。
Localizing Task Information for Improved Model Merging and Compression (2024-05-13)
ここではLocalizing Task Information for Improved Model Merging and Compression [8]で提案されているTALL MASKという手法ついて紹介します。
前提として、本論文ではパラメータ干渉をより細かい粒度で捉えており、「重みの干渉」と「タスクの干渉」に分けて考えています。その上で本質的な問題は「タスクの干渉」にあると主張しているのが本論文の特徴的な点です。
タスクの干渉が問題であると考えた背景として、Task Arithmeticを用いたマージ実験が行われています。具体的には、マージするモデル同士で重複がないようにパラメータをランダムに選択し、それぞれ選定されたパラメータのみを更新するように微調整を行い、訓練後のモデル同士をマージします。つまり、タスクに関わる重み同士は干渉しないように設定されているということです。
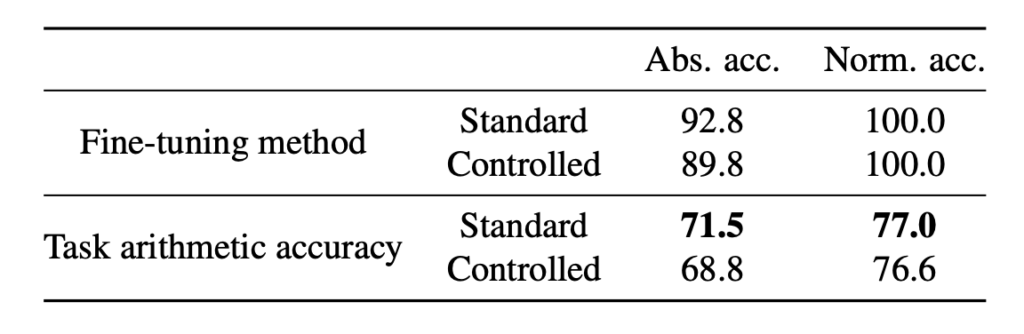
しかし実験の結果は表6の通りで、干渉しないよう設定したマージモデルは、特に操作をしていないマージモデルよりも精度が低くなりました。このようにパラメータベクトルの同じ要素の重み同士が直接的に干渉するのではなく、何らかの形でタスクを解く役割を持つ部分同士が間接的に干渉することを「タスク干渉」としてしており、この実験からマージにおける性能低下は「重み干渉」ではなく「タスク干渉」である可能性が示唆されました。
これを踏まえて本論文では、2つの考えをもとにデルタパラメータのマスクを提案しています。
- 1つ目は「破滅的な重みの削除」です。どのタスクにとっても重要でない重みはタスク間の干渉を起こす可能性があると考えられ、これらを削除することが提案されています。
- 2つ目は「自己中心的な重みの削除」です。これは特定のタスクにとっては重要であるが他のタスクには重要でない重みのことを指しており、これらがタスク干渉を起こす可能性があるとしています。
提案されているマスク手法はTALL-Maskと名付けられ、TAsk LocaLization Masksの略となっています。

まず初めに各タスクのタスクベクトル(デルタパラメータ)を取得します。これは今まで見てきた手法と同じです。次に、タスクベクトル\(\tau_t\)の総和をとった\(\tau_{\text{MTL}} = \sum\limits^T_{t=1}\tau_t\)を計算します。これをもとに以下の式で各タスクベクトルへのマスク\(m_t\)を作ります。
$$ m_t = \mathbb{1}\{|\tau_t|\geq|\tau_{\text{MTL}}-\tau_t|\cdot \lambda_t\} $$
まず、この式および本論文ではマスクは削除ではなく有効な重みとして残すと定義されていることに注意します。それを踏まえてこの式は、タスクベクトル\(\tau_t\)が大きいほど重要度が高く、残されるタスクベクトルであると読み解くことができます。また、\(\lambda_t\)は各タスクで調整可能なハイパーパラメータで、値が小さいほど多くのパラメータが有効になります。ここ得られるマスクが図16のConstructed Task Masksです。
ここで作られたマスクは以下の2つの使い道が提案されています。
- (a) Compression
- (b) Model merging
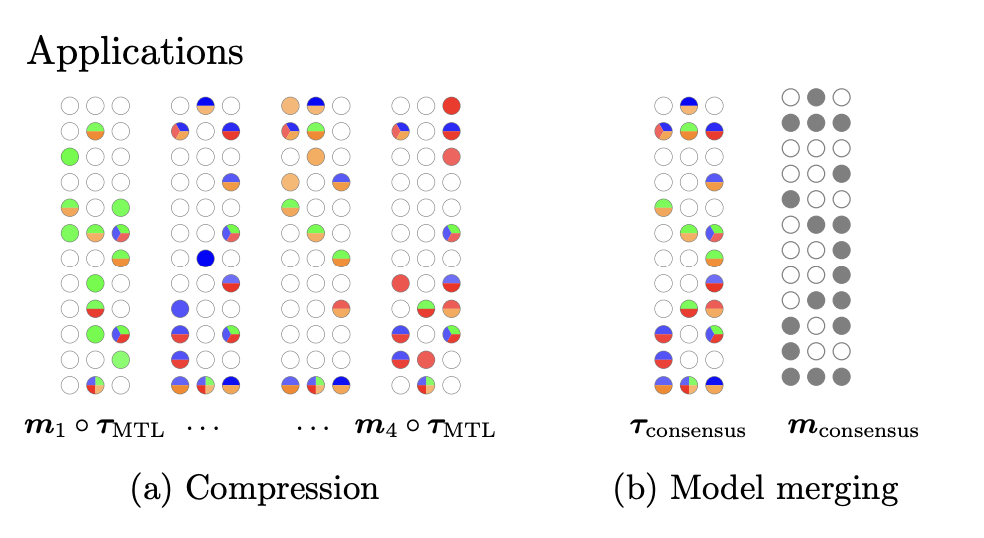
ここまでモデルマージの説明をしてきたため、わかりやすさのためにまずは2つ目のModel mergingから見ていきます。
上述した式で各タスクベクトルに対するマスク\(m_t\)が得られているとして、次のステップで行うのが、破滅的な重み(どのタスクによっても重要ではない)と自己中心的な重み(特定のタスクのみで重要)を除去するための処理です。以下の式でコンセンサスマスクを作ります。
$$ m_{\text{consensus}} = 1\bigg\{\sum\limits_{t=[T]}m_t\geq k\bigg\} $$
ここで\(k\)はハイパーパラメータであり、例えば\(k=2\)であれば少なくとも2つのタスクに対して重要である重みが有効なものとしてマスクされる(有効な重みとして残す)という理解になります。本論文では特に指定がなければ\(k=2\)を使うと述べられていますが、その根拠となるのが以下の図18です。
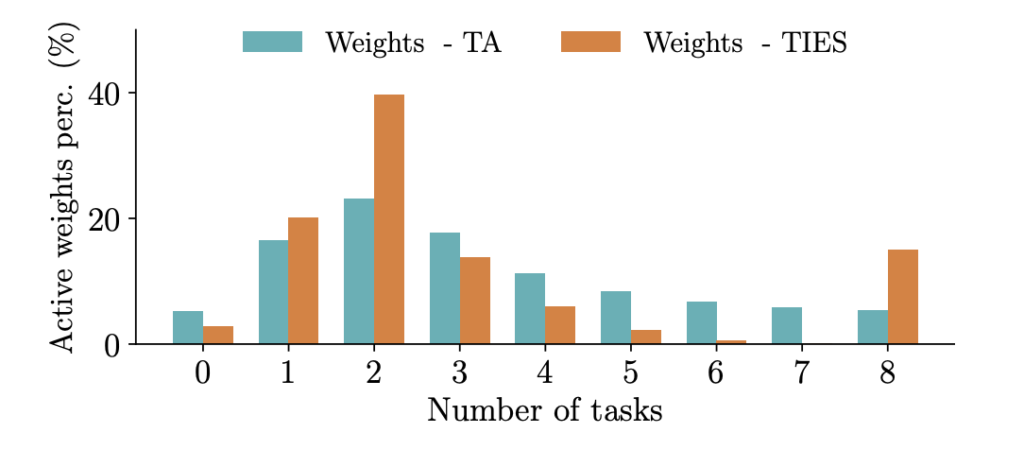
図18は8つのタスクをTask ArithmeticとTIESでマージした時のマスク(重要であるとされた重みの位置)が重複しているタスク数を横軸として、それが全体のパラメータに対してどのくらいの割合を持っていたかを縦軸としています。したがって各色はそれぞれ足して1になります。この検証結果から、タスク同士のマスクの重複がタスク数=2のときに最も多いことが示されたため、指定がなければ \(k=2\)を使うと述べられています。
最終的なモデルマージした重み\(\tau_{\text{consensus}}\)は、コンセンサスマスク\(m_{\text{consensus}}\)と初めにマージした重み\(\tau_{MTL}\)のアダマール積で算出します。
$$ \tau_{\text{consensus}} = m_{\text{consensus}} \circ \tau_{\text{MTL}} $$
ここまでがTALL Maskを用いたモデルマージの手法です。
念のため、TALL Maskのもう一つの使い道であるCompressionについても説明しておきます。ここで理解すべきことは、本手法を使うことがデータ容量の「圧縮」につながっているということです。
ここでは各タスクに対応するためにどのようにモデルを保存するかを考えます。単純な方法としては、微調整された各モデルの重み\(\theta_t\)をタスクの数だけ保存することになります。それに対して本手法では、事前学習後の重み\(\theta_0\)とマージしたタスクの重み\(\tau_{\text{MTL}}\)をベースとして保存し、各タスクのバイナリマスク\(m_t\)を保存します。このようにすると、例えばタスク\(j\)に対応したモデルを使いたい時は以下の式で重みを作ることができます。
$$ \theta_j = \theta_0 + m_j \circ \tau_{\text{MTL}} $$
このこと踏まえて保存するデータ容量について考えます。一般的に考えると、浮動小数点データ型でありデータ数(パラメータ数)が多い\(\theta_0\)や\(\theta_t\)の容量が大きく、バイナリ型であるマスク\(m_t\)の容量が小さいため、\(m_t < \tau_t = \tau_{\text{MTL}} \leq \theta_t = \theta_0\)のようになります。これを踏まえて以下の保存パターンで比較をしてみます。タスク数を \(n\) とします。
- タスクの微調整後の重みを保存する場合:\(\theta_t * n\)
\(n\)個の微調整後のモデルの重みを保存するため、タスクごとに適切なモデルを使うことができるが、保存容量が非常に大きい。 - 事前学習済みの重み + 各タスクのデルタパラメータを保存する場合:\(\theta_0 + (\tau_t * n)\)
デルタパラメータを活用する方法。事前学習済みモデルの重みと\(n\)個のデルタパラメータの重みを保存するため、保存容量は上と同じ、もしくは枝刈りをしていれば小さくなると考えられる。 - 提案手法:\(\theta_0 + \tau_{\text{MTL}} + (m_t * n)\)
事前学習済みのモデルの重み・デルタパラメータを合算したベクトル・\(n\)個のバイナリマスクを保存するため、上の2つの方法よりも保存容量は小さくなる。
上の推測から、提案手法がデータ容量の圧縮に有効であることがわかります。ただし、圧縮しているため、同じ水準で精度を担保できるとは限りません。本論文ではこれを確認する実験を行っています。
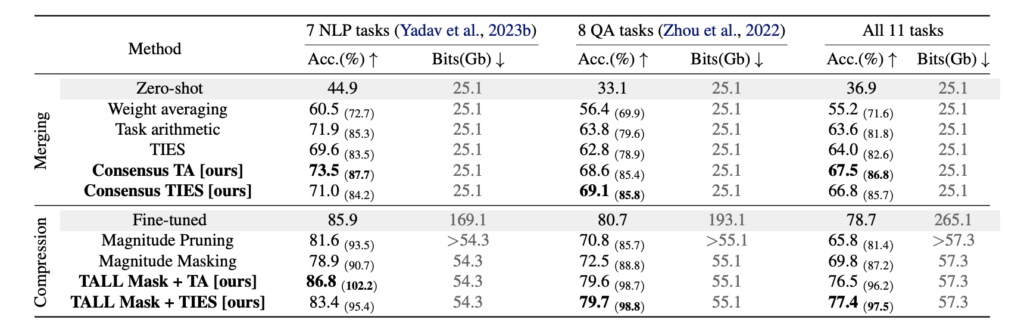
表7は提案手法であるTALL Maskを用いた実験結果であり、上段がModel mergingで作られたモデル、下段がCompressionで作られたモデルです。それぞれいくつかの手法と比較されています。(画像分類タスクの実験結果もありましたが、ここでは割愛します。)
Model mergingについては提案手法が他の手法よりも少しよい結果となっており、有効性が示されています。Compressionについては各タスクのFine-tunedと比較したときにほんの僅かに劣る結果となっています。これは「データ容量を大幅に圧縮しても性能劣化がほとんどなかった」という本手法の有効性を示しています。
DELLA-Merging: Reducing Interference in Model Merging through Magnitude-Based Sampling (2024-06-17)
ここではDELLA-Merging: Reducing Interference in Model Merging through Magnitude-Based Sampling [9]という論文で提案されているDELLAという手法を紹介します。この手法はDARE+TIESと類似したものです。枝刈り部分がDAREと異なりますが、符号一致を使ったマージはTIESの後半処理と同じものです。
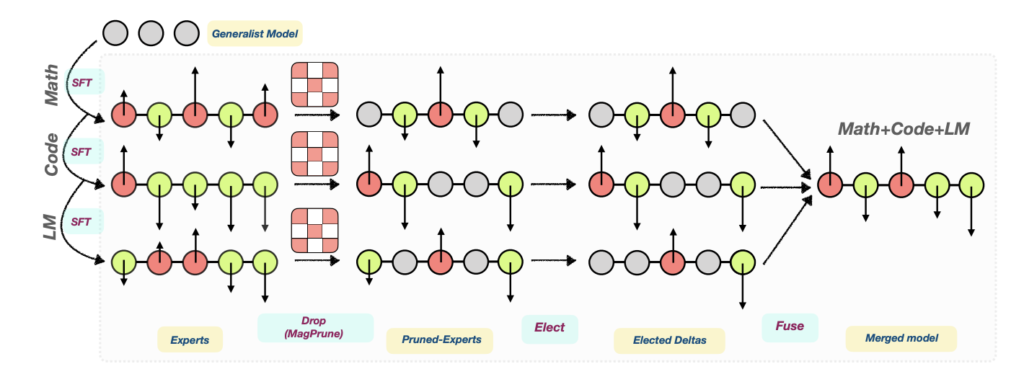
後半の処理はTIESと同じであるため割愛し、ここでは枝刈り部分を見ていきます。
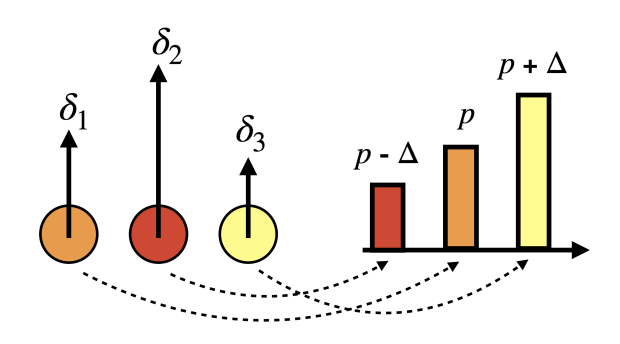
枝刈りについて、DAREではデルタパラメータをランダムにドロップし、TIESでは上位\(k\)%を残してそれ以外をドロップしていましたが、本手法では図20のようにデルタパラメータの重みの大きさにしたがってドロップする確率を与えます。
数式で見ていくと、まずデルタパラメータの各要素の絶対値の大きさにランク付けをします。
$$ \{r_1, r_2, \dots, r_n\} = \text{rank}(\{\delta_1, \delta_2, \dots, \delta_n\}) $$
このランクに基づいて以下の式でドロップ確率を設定します。ここで\(\epsilon\)はステップを意味するようなハイパーパラメータであり、大きいほどランクに対するドロップの確率差が大きくなります。(論文に直接的な記載は見られれませんでしたが、\(\epsilon\)は\(\epsilon \leq 1 – p_{\text{min}}\)を満たす必要があると思われます。こうすることで確率\(p_i\)を1以下の範囲にすることができます。)
$$ p_i = p_{\text{min}} + \frac{\epsilon}{n} \times r_i $$
最小ドロップ確率 \(p_{\text{min}}\)は以下のように設定すると求められます。これは最も重要度が高いパラメータに割り当てられるドロップ確率となります。
$$ p_{\text{min}} = p – \frac{\epsilon}{2} $$
ドロップ確率を算出した後はDAREとほとんど同じで、実際にその確率に基づいてマスクをします。違いはリスケリーリング部分にあり、DAREでは全体で同じドロップ確率\(p\)を使っていたところが、DELLAでは上で求めた\(p_i\)が使われます。
$$ m_i \sim \text{Bernoulli}(p_i) $$
$$ \tilde{\delta_i} = (1 – m_i) \odot \delta_i $$
$$ \hat{\delta_i} = \frac{\tilde{\delta_i}}{1 – p_i} $$
リスケーリング後のパラメータはTIESの後半処理と同じく符号一致を求めます。符号一致の方法としては、各モデルの同じ位置のパラメータで重みを合計し、その正負の方向でマスクを作る形です。最後に、この符号一致マスクと合致するパラメータで平均値をとることで最終的なマージの重みを決定します。
$$ \gamma^m = \text{sign}\left( \sum_{t=1}^{T} \hat{\delta}^t \right) $$
実験は言語タスク、 算数タスク、コーディングタスクで行われていました。比較対象としてはTask Arithmetic, DARE, TIESが用いられています。異なるタスク(微調整済みモデル)の組み合わせで実験を行っています。

表8の結果から、提案手法であるDELLAは、Math + Codeを除く3つのマージにおいて、タスクの平均スコアが最も良いことがわかります。TIESに劣った部分に対する考察としては、コーディングタスクを学習させた微調整モデルがそのタスクを解くための顕著なパラメータを十分に持っておらず、確率的なドロップが性能劣化につながったことが原因であると述べられています。
MetaGPT: Merging Large Language Models Using Model Exclusive Task Arithmetic (2024-06-17)
ここでは、MetaGPT: Merging Large Language Models Using Model Exclusive Task Arithmetic [10]という論文で提案されているMetaGPTという手法を紹介します。
本論文では従来のマージ手法の課題として、一般的に学習データへのアクセスが困難であることと、マージの計算コストを挙げています。データアクセスについてはModel Breadcrumbsの紹介部分で述べたように、学習に使われたデータが非公開である問題です。計算コストについては、マージそのものではなくマージを最適化しようとした時の計算コストについて言及しています。例えば2つのモデルを任意の按分で単純に重みをマージする場合、0.01刻みで按分割合を設定してグリッドサーチで探索すると、100回のマージと評価を繰り返す必要があります。これはモデルが増えるとさらに大きくなります。また、この評価のためのバリデーションデータも必要となります。このハイパーパラメータ最適化における計算コストが既存のモデルマージ手法に対する課題として主張されています。
そこで本手法では、探索を必要とすることなく最適な按分を求めるための数学的なアプローチを提案しています。詳細な導出過程は複雑であったため、詳しく知りたい方は原論文を直接ご参照いただければと思います。ここでは最適な按分を求めるためのイメージのみ説明します。
本手法の考え方は「マージ後モデルによる損失と各微調整モデルによる損失の差を最小化すること」を目指したものとなります。「各微調整モデルによる損失」は、例えばコーディングタスクを解くために微調整されたモデルの重みを使った場合の損失のことを指します。つまり、「モデルマージをした時に、各タスクに対する精度ができるだけ落ちないことを目指した手法である」と言い換えることができます。したがって、本手法はモデルマージを「損失差の最小化問題」として解くことができると述べられています。
本論文では、以下のALD(平均損失差)を最小化するように定式化されています。 この時、 \(\theta_{\text{final}}\)はマージ後のモデルのパラメータ、 \(\theta_t\)は各タスクで微調整したモデルのパラメータを意味しています。
$$ \text{ALD}(\lambda_1, \cdots, \lambda_T, \tau_1, \cdots, \tau_T) = \frac{1}{T} \sum_{t=1}^{T} \left( \mathcal{L}_t(\theta_{\text{final}}, \mathbf{x}) – \mathcal{L}_t(\theta_t, \mathbf{x}) \right) $$
このALDを最小化するために損失関数 \( \mathcal{L}_t(\theta_{\text{final}}, \mathbf{x}) \)をテイラー展開を用いて2次近似して計算しやすい形にします。(数式は本論文を参照。)
これを解いていくと、最終的に各タスクのモデルに対する最適な按分割合は以下のようになると述べられています。
$$ \lambda_t = \frac{\|\theta_t – \theta_0\|^2}{\sum_{k=1}^{n} \|\theta_k – \theta_0\|^2} $$
式を解釈すると、デルタパラメータのノルムの総和に対するタスク\(t\)のデルタパラメータのノルムの大きさによって按分の大きさが決まり、デルタパラメータベクトルが大きいほど按分が大きくなると読み取れます。また、論文中に直接的な記載はありませんでしたが、按分は他手法と同じようにモデルの各レイヤーごとに計算されるものであると考えられます。
注意として本論文では、各モデルに対するNTK線形化と、各パラメータベクトルの直行性が仮定されていると述べらています。前者はパラメータベクトルを線形に扱えることを仮定し、後者は各タスクのパラメータ干渉が抑えられていることを仮定するものです。
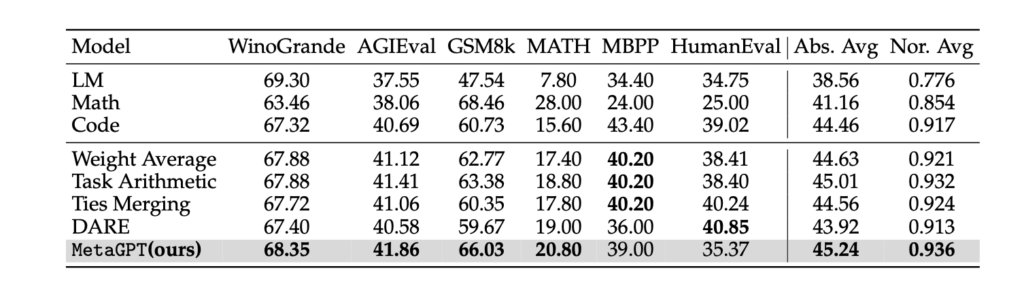
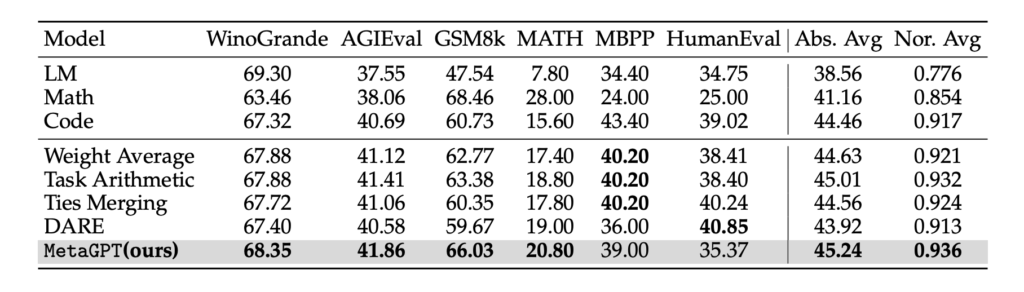
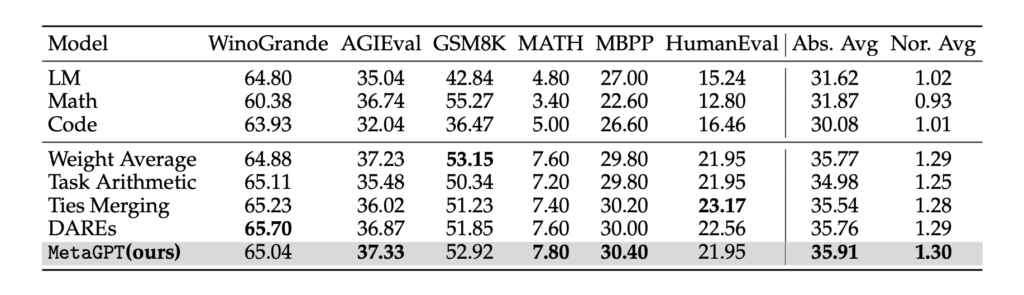
実験は3つのベースモデルを使って行われています。ベースモデルはLlama-2-7B, Mistral-7B, Llama-2-13Bが使われており、以下の表9, 10, 11がそれぞれの結果です。評価タスクは自然言語に関わるタスク、算数タスク、コーディングタスクなどが使われています。
上の結果から、本手法はいずれのモデルにおいても平均スコアで他手法をわずかに上回っていることが報告されています。
一方で、Llama-2-7BとMistral-7Bの結果に着目すると、MBPPとHumanEvalで他の手法よりも低いスコアとなっています。この2つはコーディングタスクであり、このタスクについてはDELLAでも課題となっていました。コーディングには自然言語とは異なった性質があるため、汎化性能を保ったまま有効なマージをするのが難しい傾向があると考えられます。
Model merging with SVD to tie the Knots (2024-10-25)
ここでは、Model merging with SVD to tie the Knots [11]という論文で提案されているKnOTSという手法を紹介します。
本論文はLoRAによって微調整したモデルのマージに焦点を当てており、LoRAで微調整したモデルのマージがフルパラメータチューニングによって微調整したモデルのマージよりも性能劣化が大きいという課題を示しています。
LoRAで微調整したモデルのマージがうまくいかない原因としては、LoRAの低ランク制約にあると述べられています。これを検証するためにCKA (Centered Kernal Alignment)という指標を用いています。CKAはSimilarity of Neural Network Representations Revisited [12]で提案された手法であり、ニューラルネットワークの異なる層やモデル間の表現の類似性を測定するものです。各タスクに対して、フルパラメータで微調整したモデル間におけるCKAは高い一方で、LoRAで微調整したモデル間ではCKAが低いことが明らかになりました。これは各タスクにおけるLoRAが、低ランク制約のために異なる表現空間でパラメータ更新されていることに起因していると考えられています。
これまでの先行研究ではタスクベクトルの直交性が高いほどモデルマージが上手くいくという報告が多くありました。しかし、本論文では簡単な例を用いて直交している場合でも2つのモデルが逆の予測をすることを示しており、タスクベクトルの直交性よりもそれらが同じ基底(空間)に沿っているかどうかがモデルマージにとって重要であると仮説を立てています。
これを踏まえて本論文で提案されている手法がKnOTSです。以下がそのイメージであり、この手法ではSVD (特異値分解) を用いています。
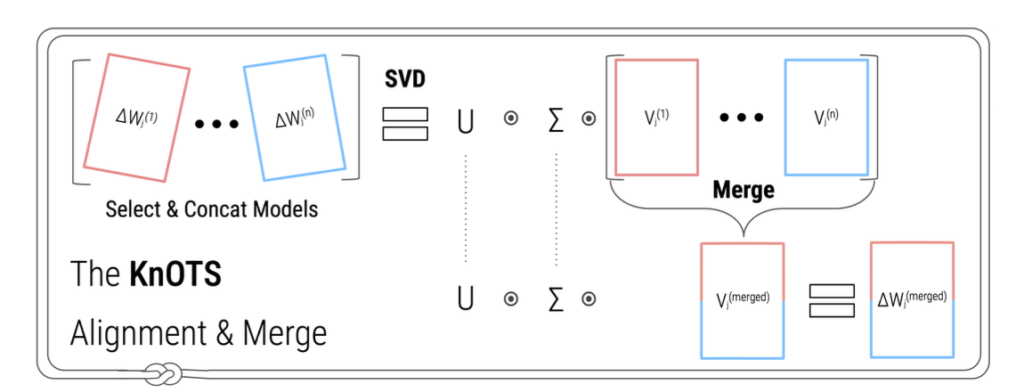
具体的には、以下の数式で示されます。 まずLoRAで微調整した各タスクモデルの重みの差分行列を列方向に結合します。(ここでの差分とはベースモデルから微調整モデルへのパラメータの重みの変化のことを指します。)
$$ \Delta W = [\Delta W^{(1)}, \Delta W^{(2)}, \ldots, \Delta W^{(n)}] $$
次に結合した一つの行列にSVD(特異値分解)を適用します。
$$ \Delta W = U \Sigma V^T $$
この時、\(U\)はすべてのタスクにおける共通の基底を表しており、 \(\Sigma\)の非負の対角値は各基底ベクトルに関連するスケールを表しており、 \(V^T\)は列方向に分割することで各タスクの個別情報を表していると解釈されます。
$$ \Delta W^{(i)} = U \Sigma [V^{(i)}]^T $$
KnOTSは、特異値分解した要素のうち \(U\Sigma\)を共通要素として用いて、各タスクに紐づく \([V^{(i)}]^T\)には既存のマージ手法(例えばTask ArithmeticやTIESなど)を適用することができると述べられています。例えば以下の式はTask Arithmeticを適用する場合の例ですが、 \(U\Sigma\)は共通要素として保持して、各タスクの \([V^{(i)}]^T\)に任意の重み \(\alpha^{(i)}\)を掛けて総和を取るマージの形となっています。
$$ \Delta W^{(\text{merged})} = U \Sigma \sum_{i=1}^n \alpha^{(i)} [V^{(i)}]^T $$
TIESを使っても同様の計算ができますが、TIESではマージの前にデルタパラメータの絶対値の大きさで枝刈りがされるため、先に \(\Sigma{V^T}\)を計算してスケール情報を持たせてから枝刈りし、残ったパラメータに対して符号一致の処理などをしてからマージをしていく処理となります。
本論文の実験結果としては、まずKnOTSを適用した場合のCKAについて確認しています。 その結果が以下の図22で示されており、LoRAを用いたときには各タスクのモデル間ではCKAが低くなっていましたが、KnOTSによるマージを適用した場合、フルパラメータチューニングほどではありませんが、CKAが改善していることがわかります。

精度実験は「タスクごとの評価」と「統合的な汎用性能の評価」に分けて実施されています。
タスクごとの評価については以下のような結果が報告されています。こちらはViT-B/32を用いた画像分類タスクでの実験結果ですが、RESISC45以外のタスクではKnOTSを適用した場合のスコアが高く、特に平均で見たときにはKnOTS + TIESを適用した場合のスコアがベースラインより4.3ポイント高いことが報告されています。(なお、スコアは \(\frac{マージモデルの正解率}{そのタスクのみで微調整されたモデルの正解率}\) という形で正規化されたスコアになっています。)
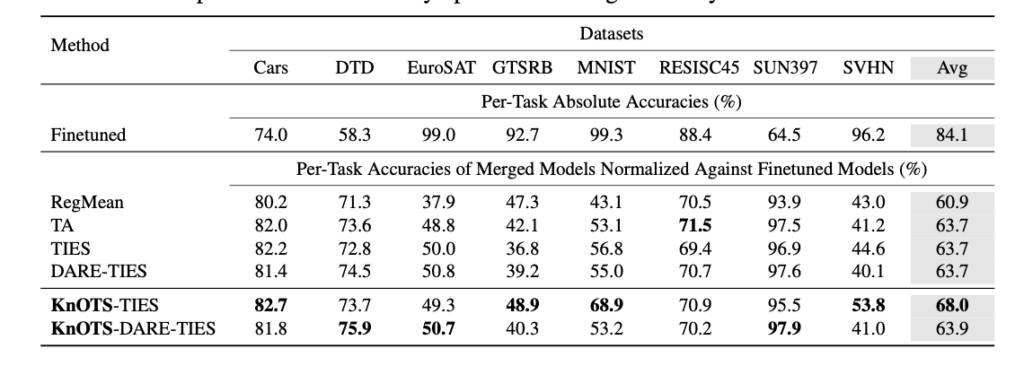
統合的な汎用性能の評価では、データセットとラベルを統合したタスクを用いて、汎用的な性能を図る試みがされています。以下の表13(a)はVit-L/14を用いた画像分類タスクの結果で、表13(b)はLlama3-8Bを用いた自然言語推論タスクの結果です。どちらにおいてもKnOTSが他手法よりも良好なスコアを示していることが報告されています。

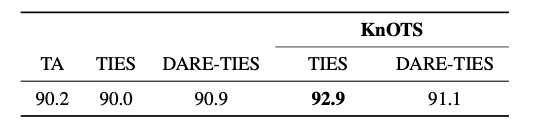
本論文ではこの他にも、KnOTSを適用したモデルの予測がアンサンブルよりも良いスコアを示したことや、本手法がマージするタスク数やLoRAのランクに対して比較的高い頑健性を持っていることが報告されています。
その他:モデルマージに関連するトピック
Evolutionary Optimization of Model Merging Recipes (2024-03-19)
ここでは[2]で提案された進化的モデルマージという手法を紹介します。これは上述してきたようなマージ手法そのものではなく、進化アルゴリズムを用いてマージのハイパーパラメータをを最適化する手法です。
例えば、実際に本論文の実験で使われているDARE-TIESを最適化する方法について説明します。DAREとTIESはそれぞれ上で紹介しました。DAREはランダムにデルタパラメータを枝刈りし、TIESは全体と符号一致するデルタパラメータをマージする手法です。
DARE-TIESを使う場合のハイパーパラメータは以下の項目です。
- どのくらいのデルタパラメータを枝刈りするのか(DAREの枝刈り割合)
- パラメータをマージするときの各モデルの対する按分はどの程度にするのか(TIESのマージ按分割合)
本論文では、これらのマージに関わるハイパーパラメータの組み合わせ数は膨大であり、経験をもとにした職人技となっていることが課題であるとして、このようなハイパーパラメータを進化アルゴリズムを使って最適化することを提案しています。具体的には、まず最適化するための評価タスクを設定し、マージ手法と最適化するハイパーパラメータを設定します。そして、評価スコアが最大になるように進化アルゴリズムを用いてハイパーパラメータを探索していくという手法となっています。
本手法の詳細や実験結果については弊社の技術記事でも解説しているため、こちらの記事もしくは本論文を直接ご参照ください。
また、弊社はお客様との共同研究として「進化的モデルマージを用いた日本語金融LLMモデルの構築」に取り組みました。参考としてこちらもぜひご覧いただければ幸いです。
MoE Merging
こちらは上で紹介してきたパラメータ空間のマージよりも、データフロー空間のマージに近い手法であると言えます。名前の通りですが、複数のモデルを用いてMoE (Mixture of Expert)のアーキテクチャを持つモデルを構築することを指します。
MoEについて簡単に説明しておきます。HuggingFaceのブログ記事 Mixture of Experts Explainedによると、MoEは主に2つの要素で構成されていると述べられています。
- 密なFFN層の代わりにスパースなMoE層を用いている。
- ゲーティングネットワークまたはルーターを持つ。
イメージとしてはSwitch Transformer [13] の図がわかりやすく、以下のような構造となっています。特徴的な点はSelf-Attentionの後にくるレイヤーであるRouterとその先の複数のFFN層です。
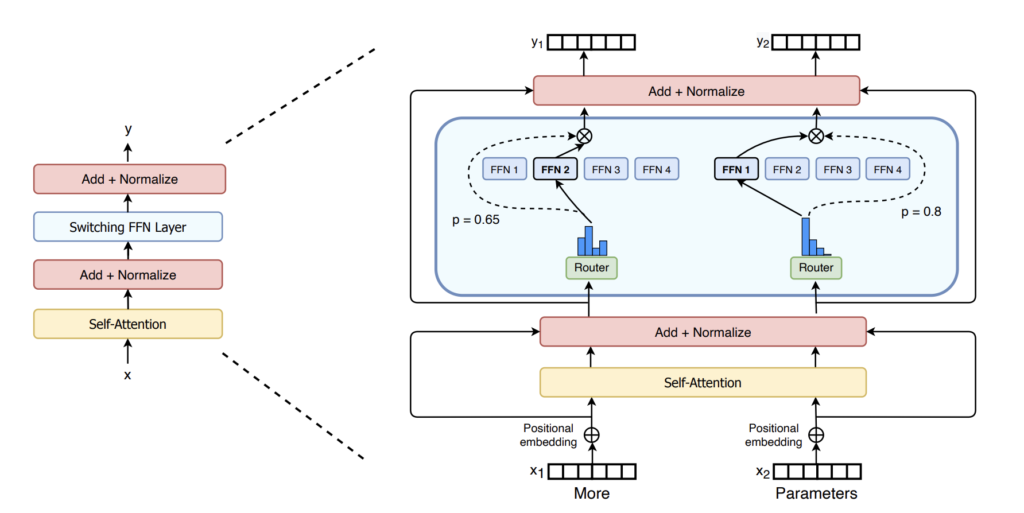
図23を見ると、FFN1 ~ FFN4のように複数のFFN層が横並びになっています。これらはエキスパートと呼ばれる部分で、MoEではトークンごとにどのエキスパートで処理するかをルーティングして、いずれかのエキスパートで処理されます。このようにすることで、各トークンごとに最適なエキスパートの重みで処理されるため、通常の密なモデルよりも高い性能が得られると言われています。また、推論時に同時に使われるパラメータ(アクティブパラメータ)は一部のエキスパートのみであるため、モデル全体のパラメータ数が大きくなっても推論速度に影響がないという強みがあります。
このMoEの構造を用いたのモデルマージの手法を提案しているのが、Branch-Train-MiX: Mixing Expert LLMs into a Mixture-of-Experts LLM [14]です。
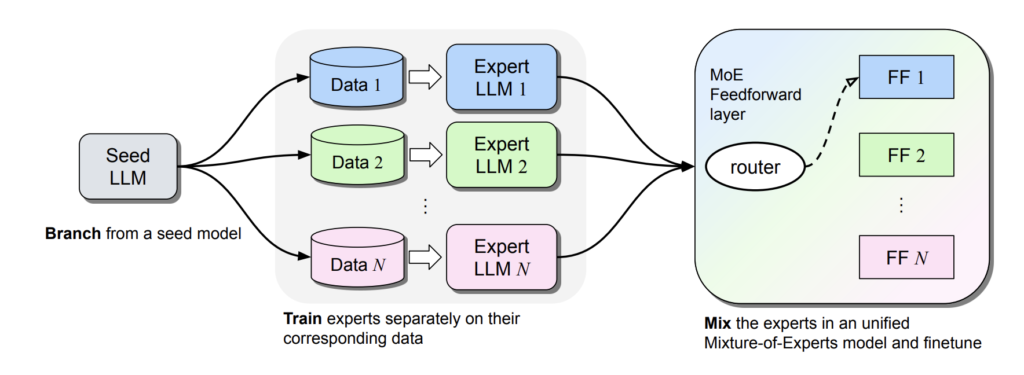
手法としてはシンプルで、まず同じベースモデルに対して各タスクに微調整したモデルを用意します。そして、各モデルのFFN層をエキスパートとしてMoE構造で組み合わせ、残りのパラメータは平均化します。
ここで、単純にマージしただけではMoEの要素であるエキスパートへのルーティングが最適化できていないため、ルーティング関数\(g\)を学習するためのパラメータである\(W_l\)を追加した以下の式でFFN層を表現し、\(W_l\)は別途ファインチューニングによって学習します。
$$ \text{FF}_{\text{MoE}}^l(x) = \sum{i=1}^{N} g_i(W_l x) \text{FF}_i^l(x) $$
本論文の実験では、数学・コーディング・ドキュメント抽出の3つのタスクでモデルを作り、また元のモデルも一つのエキスパートとして用いるため、4つのエキスパート構造として設計しています。ルーティングの学習では3つのドメインテキストに加え、事前学習に使われたテキストを用いてファインチューニングしたと述べられています。
実験結果については詳細は省きますが、一部のみ引用しておきます。注目したいのは以下の表14の最下部であり、こちらが提案手法を用いて構築したMoEモデルです。(Top-2とあるのは、FFN層で最適な2つのエキスパートにルーティングする形となっていることを意味しています。)
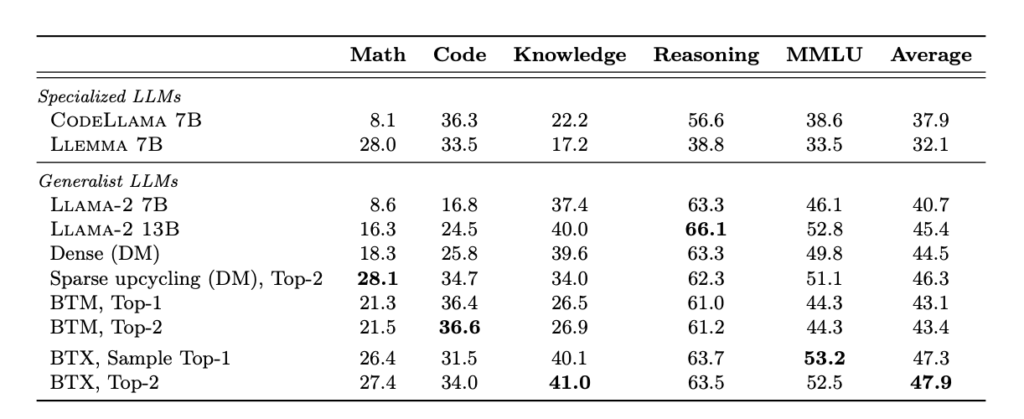
この結果を見ると、全体の平均スコアとしては元のモデルや他手法と比較して最も高い結果となっています。数学とコーディングについてはそれぞれの元モデルよりもわずかに低いスコアとなっていますが、大きく劣っているわけではなく、MoE Mergingによるモデルが比較的高い汎化性能を持っていることが報告されています。
モデルマージの実装方法
最後に、モデルマージを実装するための代表的なライブラリを紹介します。最もよく使われているのがmergekitです。こちらは環境構築してyamlファイルを設定すれば、サポートされている様々なマージ手法を用いてモデルマージを行うことができます。
任意のハイパーパラメータでマージする場合
以下はDARE-TIESを用いてマージを行う場合のサンプルコードです。ベースモデルにはmistralai/Mistral-7B-v0.1を使用します。マージするモデルとしては以下を使用します。
ここからはmergekitを用いたサンプルコードです。環境はGoogle Colabなど.ipynb形式を想定したものとなっています。マージそのものはGPUを必要としないため、CPUでも実行が可能です。
# mergekitをクローン
!git clone <https://github.com/arcee-ai/mergekit.git># 環境設定
%cd mergekit
!pip install -e .# マージモデルを出力するフォルダを作る
import os
if not os.path.exists('output'):
os.makedirs('output')# 設定ファイルを作成
yml = '''
models:
- model: augmxnt/shisa-gamma-7b-v1
parameters:
density: 0.7 # DAREの枝刈り
weight: 0.2 # TIESの按分
- model: WizardLMTeam/WizardMath-7B-V1.1
parameters:
density: 0.5
weight: 0.4
- model: HuggingFaceH4/zephyr-7b-beta
parameters:
density: 0.5
weight: 0.4
merge_method: dare_ties # マージの手法
base_model: mistralai/Mistral-7B-v0.1
parameters:
normalize: true
int8_mask: true
dtype: float16
'''
# config.ymlに書き込み
with open('./config.yml', 'w') as file:
file.write(yml)# 必要に応じてログインしておく
# モデルによってはログインしていないとダウンロードできないため
!huggingface-cli login# configと出力先を指定して実行
!mergekit-yaml ./config.yml ./output# 作成したマージモデルをHuggingFaceにアップロードしたい場合
!huggingface-cli upload your_hf_username/my-cool-model ./output .進化アルゴリズムで最適化する場合
進化的モデルマージの実装方法はこちらの記事をご参照ください。
進化的モデルマージの理解と実装 -進化的モデルマージの実装-
おわりに
今回はLLMのモデルマージ手法について紹介しました。モデルマージの課題として、マージするモデル同士が悪影響を与え合う「パラメータ干渉」が指摘されています。各手法では、この問題を解消するためにデルタパラメータの枝刈りや符号一致、またはSVDを用いた基底空間の抽出といった工夫が取り入れられていました。これらのアプローチにより、ベースラインを上回る汎化性能が示されましたが、現時点ではブレイクスルーと呼べる技術はまだ確立されていないと考えられます。
しかし、モデルマージ技術の進展は、LLMの実用化の促進に寄与する可能性があると考えています。特にドメイン特化LLMの活用において大きな役割を果たすと考えています。たとえば、企業内データを活用して事前学習や継続事前学習を行ったドメイン特化モデルに対し、対話性能を付与したい場合を考えます。この際、企業データでゼロから訓練データを構築し、ファインチューニングを行うには多大な工数とコストがかかります。一方で、モデルマージによって同等の性能を達成できるのであれば、大幅なコスト削減が可能となります。
このように、モデルマージは今後の技術の進展や活用場面によっては重要な役割を担う可能性があります。引き続き、この分野の研究動向に注目していきたいと思います。
また、LLM Merging Competitionでの取り組みや上位解法については、別記事にてご紹介する予定です。
参考文献
- [1] Yang, Enneng, et al. “Model merging in llms, mllms, and beyond: Methods, theories, applications and opportunities.” arXiv preprint arXiv:2408.07666 (2024).
- [2] Akiba, Takuya, et al. “Evolutionary Optimization of Model Merging Recipes.” arXiv preprint arXiv:2403.13187. 2024.
- [3] Wortsman, Mitchell, et al. “Model soups: averaging weights of multiple fine-tuned models improves accuracy without increasing inference time.” International conference on machine learning. PMLR, 2022.
- [4] Ilharco, Gabriel, et al. “Editing Models with Task Arithmetic.” In Proceedings of the 11th International Conference on Learning Representations (ICLR 2023). arXiv preprint arXiv:2212.04089.
- [5] Yadav, Prateek, et al. “Ties-merging: Resolving interference when merging models.” Advances in Neural Information Processing Systems 36 (2024).
- [6] Yu, Le, et al. “Language models are super mario: Absorbing abilities from homologous models as a free lunch.” Forty-first International Conference on Machine Learning. 2024.
- [7] Davari, MohammadReza, and Eugene Belilovsky. “Model breadcrumbs: Scaling multi-task model merging with sparse masks.” arXiv preprint arXiv:2312.06795 (2023).
- [8] Wang, Ke, et al. “Localizing Task Information for Improved Model Merging and Compression.” In Proceedings of the International Conference on Machine Learning. 2024.
- [9] Deep, Pala Tej, Rishabh Bhardwaj, and Soujanya Poria. “DELLA-Merging: Reducing Interference in Model Merging through Magnitude-Based Sampling.” arXiv preprint arXiv:2406.11617 (2024).
- [10] Zhou, Yuyan, et al. “MetaGPT: Merging Large Language Models Using Model Exclusive Task Arithmetic.” arXiv preprint arXiv:2406.11385 (2024).
- [11] Stoica, George, et al. “Model merging with SVD to tie the Knots.” arXiv preprint arXiv:2410.19735 (2024).
- [12] Kornblith, Simon, et al. “Similarity of neural network representations revisited.” International conference on machine learning. PMLR, 2019.
- [13] Fedus, William, Barret Zoph, and Noam Shazeer. “Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity.” Journal of Machine Learning Research 23.120 (2022): 1-39.
- [14] Sukhbaatar, Sainbayar, et al. “Branch-Train-MiX: Mixing Expert LLMs into a Mixture-of-Experts LLM.” arXiv preprint arXiv:2403.07816 (2024).
その他 参考資料
- LLM Merging Competition: Building LLMs Efficiently through Merging
- 進化的アルゴリズムによる基盤モデルの構築
- ニューラルネットワークの損失地形
- https://gist.github.com/dvschultz/3af50c40df002da3b751efab1daddf2c
- https://github.com/arcee-ai/mergekit/tree/main
- https://huggingface.co/docs/peft/developer_guides/model_merging
- Hugging Face Blog, Mixture of Experts Explained
- https://research.google/blog/do-wide-and-deep-networks-learn-the-same-things/
- https://huggingface.co/TheBloke/Llama-2-13B-fp16
- https://huggingface.co/pankajmathur/orca_mini_v3_13b
- https://huggingface.co/garage-bAInd/Platypus2-13B
- https://huggingface.co/WizardLMTeam/WizardLM-13B-V1.0
オウンドメディアも運営しています
- Meridianとは?Googleの新MMMを徹底解説!| Data Analytics Magazine (dalab.jp)
- コレスポンデンス分析とは?ビジネス活用や注意点を解説! | Data Analytics Magazine (dalab.jp)
- 因子分析とは?ビジネス活用や注意点を解説! | Data Analytics Magazine (dalab.jp)
- 需要予測とは?今すぐ役立つ分析手法・活用事例を厳選して紹介!
- MMM(マーケティング・ミックス・モデリング)とは? | Data Analytics Magazine (dalab.jp)
- 「0,1判別」の定番手法!ロジスティック回帰分析とは? | Data Analytics Magazine (dalab.jp)