Index

はじめに

データソリューション事業部の関田です。

近年、最新の技術として量子コンピューティングが話題に挙がります。しかし、日常で誰もが使用できるような量子コンピュータの実現は未だ目途が立っていません。

そんな中、量子コンピューティング技術から着想を得て、古典的に同様の計算を行うことができる古典アニーリングマシンやその計算手法が開発されてきました。そして現在ではそれらのマシンが実際に組合せ最適化問題を解く手段として用いられています。しかしながら、古典アニーリングマシンやその技術を使用するにも費用面でのハードルが高いという現状があります。

そこで登場したのがTorch Tytanです。Torch Tytanは2024年3月時点で、CPUやGPUを用いてローカル環境で無料で使用することができます。古典アニーリングマシン同様、量子状態を扱うわけではありませんが、量子アニーリングマシンと同じ定式化で最適化問題を解くことができます。

1. QUBOアニーリング

量子コンピューティングの計算方法は、大きく分けてゲート型とアニーリング型の二種類があります。さらにアニーリング型の中でも、QUBO形式やイジングモデルといった定式化手法が存在します。

QUBOアニーリングでは、QUBO形式で表される以下の式（ハミルトニアン、目的関数）を最小化する変数 \(q_i\) の組を探索します。

\[H(q) = \sum_{i,j} Q_{i,j} q_i q_j + \sum_i b_i q_i\]

ここで、\(q_i\) は0または1の値を取る変数、\(Q_{i,j}\) と \(b_i\) はそれぞれ二次、一次の項の係数です。
QUBO形式での定式化についての解説は「イジングマシンで解く最適化問題の定式化」を参照ください。

2. Torch Tytan

今回紹介するTorch Tytanは、PyTorchをバックエンドとしてQUBOアニーリングの最適化手法を模倣したSDKです。
計算にはGPUまたはCPUを使用しており、本当の量子状態を扱っているわけではありません。しかし近年のGPUの進化は凄まじく、それに伴ってGPUを使用するTorch Tytanも進化していきます。サンプラーが追加されるなどのアップデートが日々されているので、今後さらに使いやすくなることが期待されます。

3. 実装

3.1. 問題設定

以前書いた記事「イジングマシンで解く最適化問題の定式化」の例題をQUBOで解きます。

上の記事内ではイジングモデルで定式化しましたが、ここではQUBOで定式化して解くことができることをお見せします。

設定：
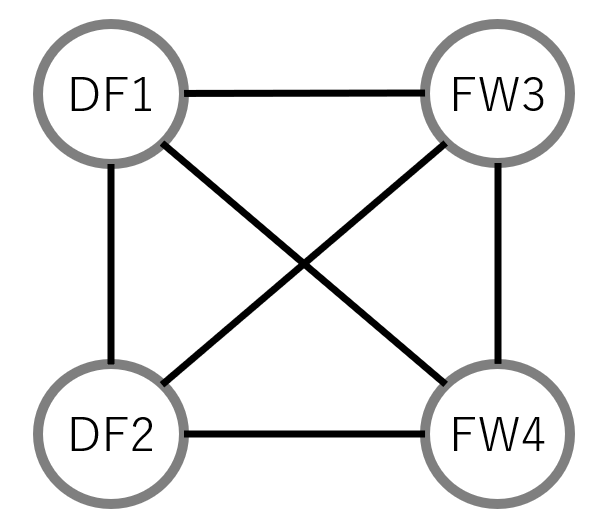
4人でサッカー対戦を行う。集まった4人には、図の通りポジションが割り当てられている。

問題：
次の条件をなるべく満たすようにチーム分けを行う。

条件：
・チーム内でポジションが偏らないようにする
・各チームの人数が平等になるようにする

図. 4人のポジションと番号。DFやFWがポジション名で、その後の数字が個人を識別する番号。

3.2. コードと解説

コードサンプルは以下の通りとなります（Google Colaboratoryでの動作を想定しています）。

!pip install -U git+https://github.com/tytansdk/tytan
from tytan import *

#量子ビット数を定義
N = 4

#量子ビットを用意（まとめて定義）
q = symbols_list(N, format_txt='q{}')
print(q)
print("それぞれ0または1の値を取る。")
print("q0: DF1が入るチーム, q1: DF2が入るチーム, q2: FW3が入るチーム, q3: FW4が入るチーム　とする。")
print("4人をteam0とteam1に割り振る。")
print()

#ハミルトニアン（最小化したい目的関数）を定義
H = (q[0] + q[1] - 1 )**2 + (q[2] + q[3] - 1 )**2 + (q[0] + q[1] + q[2] + q[3] - 2)**2

#コンパイル
qubo, offset = Compile(H).get_qubo()

#サンプラー選択（乱数シード固定）
solver = sampler.SASampler(seed=0)

#サンプリング（100回）
result = solver.run(qubo, shots=100)

#チーム分けを表示（output用処理）
def replace_dict_keys(input_dict, replacements):
    # 置換後のdictを初期化
    result_dict = {}

    # 元のdictを走査しながらkeyを置換
    for old_key, value in input_dict.items():
        new_key = replacements.get(old_key, old_key)  # keyが置換テーブルに存在する場合は置換後のkeyを使用し、存在しない場合は元のkeyをそのまま使用
        result_dict[new_key] = value

    return result_dict

replace_dict = {"q0": "DF1", "q1": "DF2", "q2": "FW3", "q3": "FW4"}
print("最適なチームの分け方を全て出力")
for r in result:
  replaced = replace_dict_keys(r[0], replace_dict)
  team0 = [key for key, value in replaced.items() if value == 0]
  team1 = [key for key, value in replaced.items() if value == 1]
  print("team0:", team0, ",", "team1:", team1)

上記を実行すれば、以下のような出力が得られます。

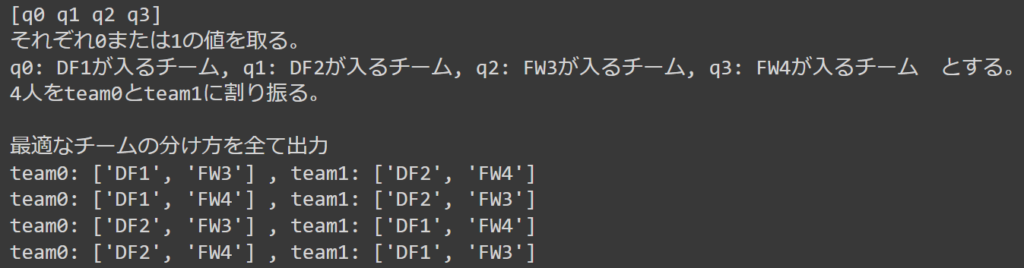
コードをもう少し細かく見ていきましょう。

インストール、インポートします。

!pip install -U git+https://github.com/tytansdk/tytan
from tytan import *

ビットを設定します。

今回は各人に各ビットを割り当てることにして、4ビット用意します。人（DF1, DF2, FW3, FW4）とビット（q0, q1, q2, q3）の対応関係は出力の通りです。ビットなので4つ変数はそれぞれ0または1のいずれかの値を取ります。0または1の値は、team0とteam1という2チームに対応付けることにします。

#量子ビット数を定義
N = 4

#量子ビットを用意（まとめて定義）
q = symbols_list(N, format_txt='q{}')
print(q)
print("それぞれ0または1の値を取る。")
print("q0: DF1が入るチーム, q1: DF2が入るチーム, q2: FW3が入るチーム, q3: FW4が入るチーム　とする。")
print("4人をteam0とteam1に割り振る。")

出力：

目的関数の定式化を行います。

定式化について簡単に解説します。
まずは一項目について考えます。DF1 (q0) とDF2 (q1) は同じポジションなので、別チームに属してほしいです。つまりq0とq1は一方が0、もう一方が1となってほしいです。これを目的関数が小さくなるように定式化するために、\((q0 + q1 – 1)^2\)と表します。こうすれば、一方が0でもう一方が1のときに最小値0を取ります。

二項目はFW3とFW4について同様に定式化したものです。

最後に三項目についてです。4人が2人ずつ2チームに分かれるためには、2人が0、他の2人が1の値を持てば良いです。\((q0 + q1 + q2 + q3 – 2)^2\)という表式は、2人が0、他の2人が1の値を持つときに最小値0となります。

#ハミルトニアン（最小化したい目的関数）を定義
H = (q[0] + q[1] - 1 )**2 + (q[2] + q[3] - 1 )**2 + (q[0] + q[1] + q[2] + q[3] - 2)**2

定式化した目的関数を最小化する処理を書きます。

コンパイル、サンプラーの設定、サンプリングを行います。

#コンパイル
qubo, offset = Compile(H).get_qubo()

#サンプラー選択（乱数シード固定）
solver = sampler.SASampler(seed=0)

#サンプリング（100回）
result = solver.run(qubo, shots=100)

最終出力の処理を書きます。

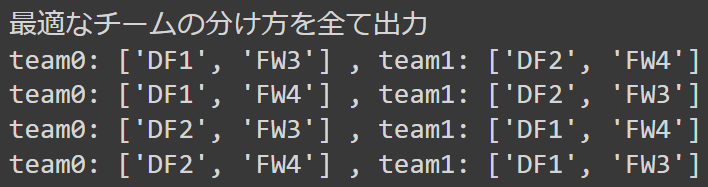
4つの解が出てきましたが、すべて問題設定の条件を満たしていることが確認できます。

#チーム分けを表示（output用処理）
def replace_dict_keys(input_dict, replacements):
    # 置換後のdictを初期化
    result_dict = {}

    # 元のdictを走査しながらkeyを置換
    for old_key, value in input_dict.items():
        new_key = replacements.get(old_key, old_key)  # keyが置換テーブルに存在する場合は置換後のkeyを使用し、存在しない場合は元のkeyをそのまま使用
        result_dict[new_key] = value

    return result_dict

replace_dict = {"q0": "DF1", "q1": "DF2", "q2": "FW3", "q3": "FW4"}
print("最適なチームの分け方を全て出力")
for r in result:
  replaced = replace_dict_keys(r[0], replace_dict)
  team0 = [key for key, value in replaced.items() if value == 0]
  team1 = [key for key, value in replaced.items() if value == 1]
  print("team0:", team0, ",", "team1:", team1)

出力：

3.3. おまけ

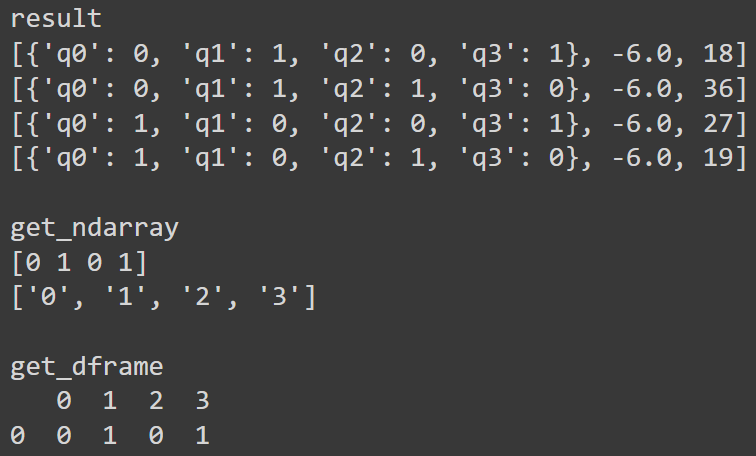
辞書、ndarrayやDataFrameといった様々な形式での出力が簡単にできます。

#すべての結果を確認
print('result')
for r in result:
    print(r)
print()

#1つ目の結果を自動配列で確認（ndarray形式）
arr, subs = Auto_array(result[0]).get_ndarray('q{}')
print('get_ndarray')
print(arr)
print(subs)
print()

#1つ目の結果を自動配列で確認（DataFrame形式）（1次元、2次元のみ）
df, subs = Auto_array(result[0]).get_dframe('q{}')
print('get_dframe')
print(df)
print()

出力：

4. おわりに

Google Colaboratoryで簡単にQUBO形式の最適化を実装できました！
2024年3月時点では、無料のローカルサンプラーだと1,000ビット程度までしか対応していないようですが、頻繁にアップデートしているので近いうちにもっと拡張されるかもしれません。
商用クラウドサンプラーを使用すれば最大で100,000ビットまで対応可能なようですので、本格的に使用することもできます。もし最適化したいことがあったら試しに使ってみてはいかがでしょうか！

Torch TytanによるQUBOアニーリング実装