Index

はじめに
1. 量子フーリエ変換の計算
- 1.1. 量子フーリエ変換の導入
- 1.2. 量子フーリエ変換の導出
2. 量子フーリエ変換を行う量子回路
- 2.1. 量子ゲートの導入
- 2.2. 量子回路の作成
おわりに
A. 付録
- A.1. 量子フーリエ変換のユニタリ性
- A.2. 量子ゲートはなぜユニタリ性を要求するのか
参考
オウンドメディアも運営しています

はじめに

　データソリューション事業部の関田です。

　今回は量子計算で最も重要なテクニックの一つである量子フーリエ変換について、数式と量子回路の導出を行います。

　量子フーリエ変換はその名の通り、量子計算を用いてフーリエ変換を行う手法です。これは古典的な離散フーリエ変換よりも計算量が少ないことが証明されており、Shorのアルゴリズムなど様々な量子アルゴリズムのサブルーチンとして組み込まれています。したがって、量子アルゴリズムを理解するためには量子フーリエ変換の理解が欠かせません。

　本記事では、量子アルゴリズムを勉強中の方に向けて、途中式や式と量子回路との対応付けを詳細に解説していきます。

　以下の知識を持っていると読みやすいです。

線形代数を中心とした大学レベルの数学
2量子ビットゲートなど量子ゲートの基礎

1. 量子フーリエ変換の計算

　まずは、量子フーリエ変換の計算について詳しく解説します。

1.1. 量子フーリエ変換の導入

　$2^n$ 次元の複素ベクトル $\lbrace x_j \rbrace \ (j \in \lbrace 0, 1, \dots, 2^n-1 \rbrace)$ の離散フーリエ変換 $\lbrace y_k \rbrace \ (k \in \lbrace 0, 1, \cdots, 2^n-1 \rbrace)$ を以下で定義します。

$$ y_k := \frac{1}{\sqrt{2^n}} \sum^{2^n-1}_{j=0} x_j e^{2\pi ikj/2^n} \tag{1}$$

ただし、$\lbrace x_j \rbrace$ は以下のように規格化されているとします。

$$ \sum^{2^n-1}_{j=0}|x_j|^2 = 1$$

規格化している理由は、量子回路の入力に対応させるためです。

　量子フーリエ変換の目標は、入力の量子状態 $\left| x \right\rangle$ を出力の量子状態 $\left| y\right\rangle$ へ変換することです。ここで、各状態はそれぞれ以下で表されるものとします。

$$ \left| x \right\rangle := \sum^{2^n-1}_{j=0} x_j \left| j \right\rangle, $$

$$ \left| y \right\rangle := \sum^{2^n-1}_{k=0} y_k \left|k \right\rangle \tag{2} $$

ここでは、$\left| i \right\rangle$ は10進数表記と2進数表記の両方を用います。文脈によっていずれか便利な方を用いるので注意が必要です。

💡 表記の具体例
　量子ビットを $n=2$ 個用意します。このとき状態 $\left| i \right\rangle$ は以下の4通りの値を取りうることがわかります。

$\left| 0 \right\rangle_{(10)} = \left| 00 \right\rangle_{(2)}$
$\left| 1 \right\rangle_{(10)} = \left| 01 \right\rangle_{(2)}$
$\left| 2 \right\rangle_{(10)} = \left| 10 \right\rangle_{(2)}$
$\left| 3 \right\rangle_{(10)} = \left| 11 \right\rangle_{(2)}$

また、$\left| i \right\rangle$ は各量子ビットの状態なので、正規直交基底となります。

それでは、入力の量子状態 $\left| x \right\rangle$ を出力の量子状態 $\left| y\right\rangle$ へ変換することを考えます。まずは式 $(1)$ を式 $(2)$ へ代入します。

$$\begin{align*} \left| y \right\rangle &= \sum^{2^n-1}_{k=0} \frac{1}{\sqrt{2^n}} \sum^{2^n-1}_{j=0} x_j e^{2\pi ikj/2^n} \left|k \right\rangle\\ &=\sum^{2^n-1}_{j=0} x_j \biggl( \frac{1}{\sqrt{2^n}} \sum^{2^n-1}_{k=0} e^{2\pi ikj/2^n} \left|k \right\rangle \biggr) \end{align*}$$

これを入出力状態と見比べることにより、量子フーリエ変換では以下の変換を行う行列 $U_{\rm{QFT}}$ を見つければよいことがわかります。

$$ U_{\rm{QFT}}\left|j \right\rangle = \frac{1}{\sqrt{2^n}} \sum^{2^n-1}_{k=0} e^{2\pi ikj/2^n} \left|k \right\rangle \tag{3}$$

この $U_{\rm{QFT}}$ による変換を量子フーリエ変換と呼びます。またこの変換がユニタリであることは付録A.1.で証明します。

1.2. 量子フーリエ変換の導出

　次に量子フーリエ変換の具体的な操作、つまり、式 $(3)$ の具体的な表式を求めにいきます。

ここから、$\left|j \right\rangle = \left| j_1 j_2 j_3 \cdots j_n \right\rangle (j_k \in \lbrace 0, \ 1\rbrace)$ と表記します。つまり、量子状態を明示的に2進数表記します。このとき、10進数での $j$ と2進数での $j_1 j_2 j_3 \cdots j_n$ には以下の関係があります。

$$ \begin{align*}
j_{(10)} &= j_1 j_2 j_3 \cdots {j_n}_{(2)} \\
&= (j_1 2^{n-1} + j_2 2^{n-2} + \cdots + j_n2^0) _{(10)}
\end{align*}$$

この表記を用いると、2の累乗での $j$ の割り算が以下のような小数で表されます。

$$ \begin{align*}
\frac{j}{2^l}
&= \frac{j_1 j_2 j_3 \cdots {j_n}}{2^l} \\
&= j_1j_2\cdots j_{n-l}.j_{n-l+1} \cdots j_n \quad \text{for $\hspace{2.5mm} l = 1, \cdots, n-1$} \end{align*} $$

$l=n$ の場合は先頭に0を置いて $0.j_1\cdots j_n$ となります。さらに、オイラーの公式より以下の場合に $j_1j_2\cdots j_{n-l}.j_{n-l+1} \cdots j_n$ の整数部分は無視できます。

$$ \begin{align*}
e^{2\pi i j/2^l}
&= e^{2 \pi i ( j_1j_2\cdots j_{n-l}.j_{n-l+1} \cdots j_n)} \\
&= e^{2 \pi i ( j_1j_2\cdots j_{n-l})} e^{2 \pi i (0.j_{n-l+1} \cdots j_n)} \\
&= 1 \times e^{2 \pi i (0.j_{n-l+1} \cdots j_n)} \quad \because{オイラーの公式} \\
&= e^{2 \pi i （0.j_{n-l+1} \cdots j_n)}
\end{align*} $$

以上に注意すると、式 $(3)$ の右辺は以下のように表されます (規格化定数は略) 。

$$ \begin{align*} \sum^{2^n-1}_{k=0} e^{2\pi ikj/2^n} \left|k \right\rangle &= \sum^{1}_{k_1=0} \sum^{1}_{k_2=0} \cdots \sum^{1}_{k_n=0} e^{2\pi i (k_1 2^{n-1} + k_2 2^{n-2} + \cdots + k_n2^0) j/2^n} \left | k_1 k_2 \cdots k_n \right\rangle \\ &= \sum^{1}_{k_1=0} \sum^{1}_{k_2=0} \cdots \sum^{1}_{k_n=0} e^{2 \pi i (k_1 2^{-1}+ k_2 2^{-2} + \cdots + k_n 2^{-n})j} \left | k_1 k_2 \cdots k_n \right\rangle \\ &= \biggl( \sum_{k_1=0}^1 e^{2\pi ik_1 2^{-1}j} \left| k_1 \right\rangle \biggr) \otimes \biggl( \sum_{k_2=0}^1 e^{2\pi ik_2 2^{-2}j} \left| k_2 \right\rangle \biggr) \otimes \cdots \otimes \biggl( \sum_{k_n=0}^1 e^{2\pi ik_n 2^{-n}j} \left| k_n \right\rangle \biggr) \\ &= (\left| 0 \right\rangle + e^{2\pi i (j_1 j_2 \cdots j_{n-1}.j_n)}\left| 1 \right\rangle) \otimes (\left| 0 \right\rangle + e^{2\pi i (j_1 \cdots j_{n-2}. j_{n-1}j_n)}\left| 1 \right\rangle) \otimes \cdots \\ & \qquad \otimes (\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle) \\ &= (\left| 0 \right\rangle + e^{2\pi i (0.j_n)}\left| 1 \right\rangle) \otimes (\left| 0 \right\rangle + e^{2\pi i (0. j_{n-1}j_n)}\left| 1 \right\rangle) \otimes \cdots \otimes (\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle) \end{align*}$$

最終的に、式 $(3)$ すなわち量子フーリエ変換は以下のような変換を行えばよいことがわかります。

$$ \begin{align*}
U_{\rm{QFT}}\left|j \right\rangle
&= U_{\rm{QFT}} \left| j_1 \cdots j_n \right\rangle \\
&= \frac{1}{\sqrt{2^n}} (\left| 0 \right\rangle + e^{2\pi i (0.j_n)}\left| 1 \right\rangle) \otimes (\left| 0 \right\rangle + e^{2\pi i (0. j_{n-1}j_n)}\left| 1 \right\rangle) \otimes \cdots \\
& \quad \quad \otimes (\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle) \tag{4}
\end{align*} $$

　ここで改めて式の意味を確認します。 $j_1, j_2, \cdots, j_n$ はそれぞれ1つの入力量子ビットに対応しており、状態 $\left| j_1 \cdots j_n \right\rangle$ は $n$ 個の量子ビットから成る変換前（入力時）の回路全体の状態を表します。量子フーリエ変換による変換後、各量子ビットは $\frac{1}{\sqrt{2}}(\left| 0 \right\rangle + e^{2\pi i (0.j_n)}\left| 1 \right\rangle),\cdots, \frac{1}{\sqrt{2}}(\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle)$ の状態を取り、回路全体として式 $(4)$ の状態になっています。

2. 量子フーリエ変換を行う量子回路

　ここでは、式 $(4)$ を実行する量子回路の構成を考えます。

2.1. 量子ゲートの導入

　まずは準備として、アダマールゲート $H$ と回転ゲート $R_k$ を導入しておきます。それぞれ以下で定義します。

$$ \begin{align*} H := \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \end{align*} $$

$$ \begin{align*} R_k := \begin{pmatrix} 1 & 0 \\ 0 & \exp\left(\frac{2\pi i}{2^k}\right) \end{pmatrix} \end{align*} $$

証明は省略しますが、これらは共にユニタリ行列です。自身の随伴行列との積が単位行列になることが確認できるはずです。

💡 アダマールゲートと回転ゲートの具体的な操作
　各ゲートを状態 $\left|0\right\rangle, \left|1\right\rangle$ に作用させることで、以下の通り新たな状態を得ます。

アダマールゲート

$$ \begin{align*} H\left|0\right\rangle &= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\ &= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} \\ &= \frac{\left|0\right\rangle + \left|1\right\rangle}{\sqrt{2}} \end{align*} $$

$$ H\left|1\right\rangle = \frac{\left|0\right\rangle – \left|1\right\rangle}{\sqrt{2}} $$

$H$ ゲートの変換はまとめて次のように書くことができます。

$$ H\left|j\right\rangle = \frac{\left|0\right\rangle + e^{2\pi i (0.j)}\left|1\right\rangle}{\sqrt{2}} $$

回転ゲート

$$ R_k\left|0\right\rangle = \left|0\right\rangle $$

$$ R_k\left|1\right\rangle = \exp\left(\frac{2\pi i}{2^k}\right) \left|1\right\rangle $$

$R_k$ ゲートの変換はまとめて次のように書くことができます。

$$ R_k\left|j\right\rangle=\exp{\left(\frac{2\pi i j}{2^k}\right)}\left|j\right\rangle \tag{5} $$

これらの変換を用いて、量子フーリエ変換を実現します。

2.2. 量子回路の作成

　式とそれに対応する量子回路を並行して見ていきましょう。

ステップA

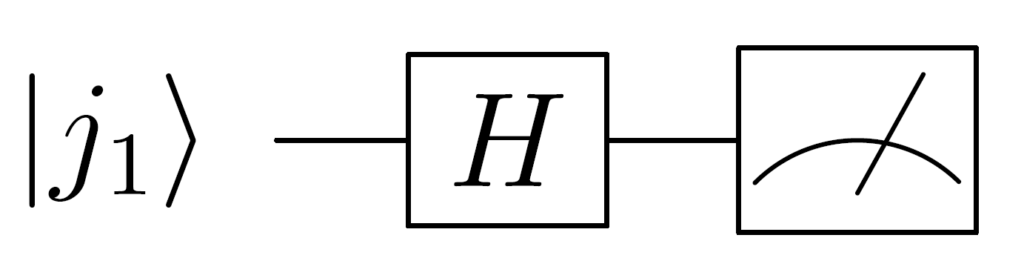
　式 $(4)$ の $n$ 番目の状態 $\frac{1}{\sqrt{2}}(\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle)$ を作ることを考えます。変換元である状態 $\left| j_1 \cdots j_n \right\rangle$ の1番目の状態 $\left|j_1\right\rangle$ に $H$ ゲートを作用させると、以下のように変換されます。

$$ H\left| j_1 \cdots j_n \right\rangle = \frac{1}{\sqrt{2}}\left(\left|0\right\rangle + e^{2\pi i (0.j_1)}\left|1\right\rangle\right)\left| j_2 \cdots j_n \right\rangle $$

図1. 状態 $\left|j_1\right\rangle$ に $H$ ゲートを作用させた回路図

さらに、2番目の状態 $\left|j_2\right\rangle$ を制御ビット、1番目の上記の変換後の状態を標的ビットとして$R_2$ ゲートを作用させます。このような2量子ビットゲート $R_2$ は以下のように動作します。

制御ビット $\left|j_2\right\rangle$ が $\left|1\right\rangle$ のとき、標的ビットの状態 $\left|1\right\rangle$ を $\exp({\frac{2\pi i}{4}})$ 倍し、状態 $\left|0\right\rangle$ は変化させない
制御ビット $\left|j_2\right\rangle$ が $\left|0\right\rangle$ のとき、標的ビットの状態を変化させない

まとめると、式では $\left|1\right\rangle$ に $\exp({2\pi i(j_2/4)})=\exp({2\pi i(0.0j_2)})$ （右辺で $j_2/4$ を2進数表記）をかければよいことがわかります。なお、これは式 $(5)$ と同義です。

$$ \begin{align*} R_2\frac{1}{\sqrt{2}}\left(\left|0\right\rangle + e^{2\pi i (0.j_1)}\left|1\right\rangle\right)\left| j_2 \cdots j_n \right\rangle &= \frac{1}{\sqrt{2}}\left(\left|0\right\rangle + e^{2\pi i(0.0j_2)}e^{2\pi i (0.j_1)}\left|1\right\rangle\right)\left| j_2 \cdots j_n \right\rangle \\ &= \frac{1}{\sqrt{2}}\left(\left|0\right\rangle + e^{2\pi i (0.j_1j_2)}\left|1\right\rangle\right)\left| j_2 \cdots j_n \right\rangle \end{align*} $$

この操作を表す回路図は以下の通りです。

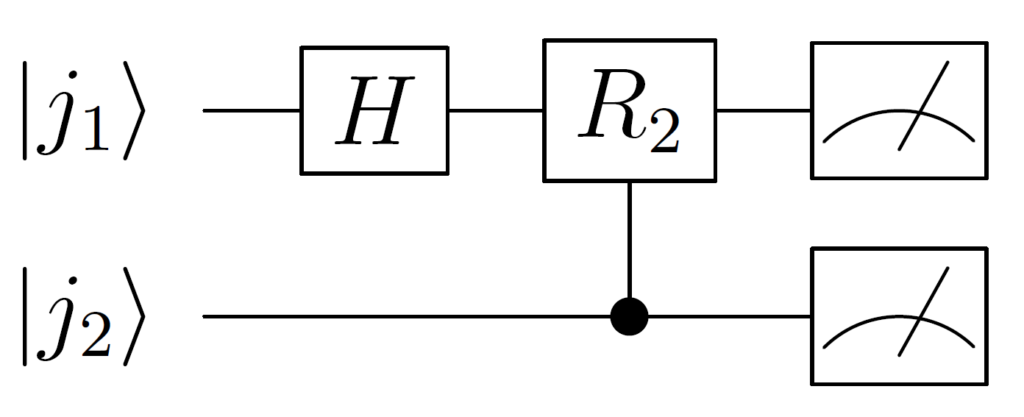
図2. 状態 $\left|j_2\right\rangle$ を制御ビット、アダマール変換後の状態 $\left|j_1\right\rangle$ を標的ビットとする $R_2$ ゲートを作用させた回路図

同様に、3番目の状態 $\left|j_3\right\rangle$ を制御ビット、1番目の上記の変換後の状態を標的ビットとして$R_2$ ゲートを作用させると、以下のように変換されます。

$$ \begin{align*} R_3\frac{1}{\sqrt{2}}\left(\left|0\right\rangle + e^{2\pi i (0.j_1j_2)}\left|1\right\rangle\right)\left| j_2 \cdots j_n \right\rangle = \frac{1}{\sqrt{2}}\left(\left|0\right\rangle + e^{2\pi i (0.j_1j_2j_3)}\left|1\right\rangle\right)\left| j_2 \cdots j_n \right\rangle \end{align*} $$

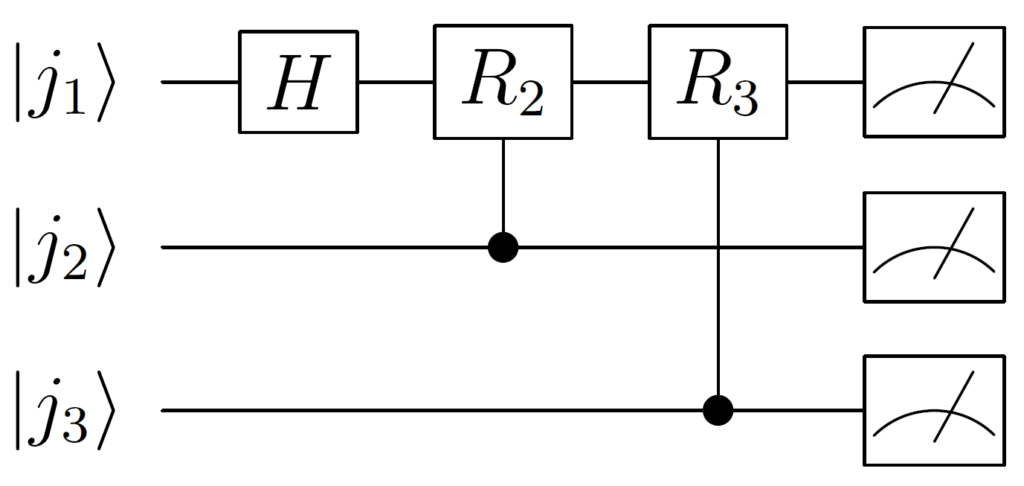
同じ計算を $n$ 番目の制御ビットまで繰り返すことにより、以下の状態を得ます。

$$ \frac{1}{\sqrt{2}}(\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle)\left|j_2 \cdots j_n \right\rangle $$

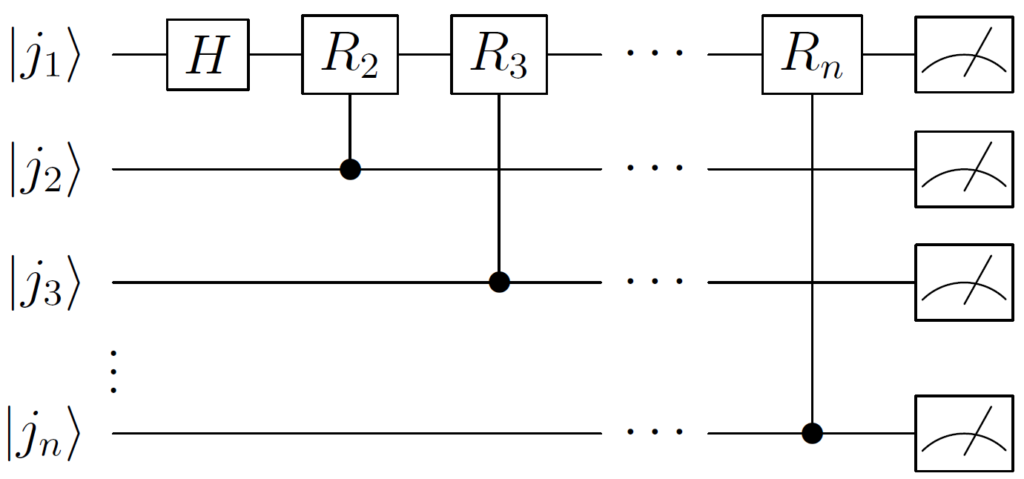
上の状態は1番目の量子ビット $\left|j_1\right\rangle$ を変換させていった結果なので、上記変換後に1番目の量子ビットを測定することで、状態 $\frac{1}{\sqrt{2}}(\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle)$ を得ることができます。
これが式 $(4)$ の $n$ 番目の状態です。

ステップB

　式 $(4)$ の $(n-1)$ 番目の状態は、先ほどの $(\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle)$ から $j_1$ を除き $j_2$ を小数部分の先頭にしたものです。したがって、$(n-1)$ 番目の状態を得るためには、ステップAで $j_1$ を基準に考えていた所を $j_2$ に置き換えればよいことが類推できます。

同じ手続きではありますが、一部の計算を記載します。

ステップAで作成した状態の $\left|j_2\right\rangle$ に $H$ ゲートを作用させます。

$$ \begin{align*} &H\frac{1}{\sqrt{2}}(\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle)\left|j_2 \cdots j_n \right\rangle \\ &= \frac{1}{\sqrt{2}}(\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle) \otimes \frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi i (0.j_2)}\left|1\right\rangle)\left|j_3 \cdots j_n \right\rangle \end{align*} $$

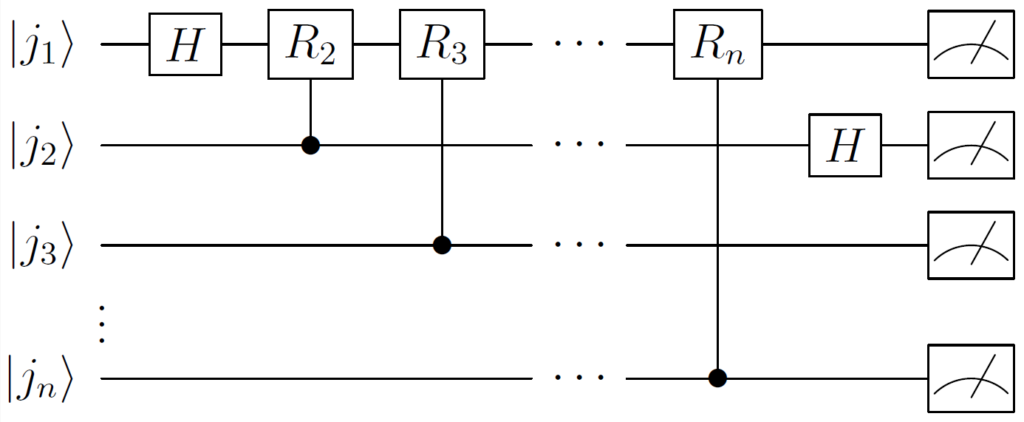
図5. 状態 $\left|j_2\right\rangle$ に $H$ ゲートを作用させた回路図

続いて、状態 $\left|j_3\right\rangle$ を制御ビット、アダマール変換後の状態 $\left|j_2\right\rangle$ を標的ビットとする $R_2$ ゲートを作用させます。

$$ \begin{align*} &R_2\frac{1}{\sqrt{2}}(\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle) \otimes \frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi i (0.j_2)}\left|1\right\rangle)\left|j_3 \cdots j_n \right\rangle \\ &= \frac{1}{\sqrt{2}}(\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle) \otimes \frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi i (0.j_2j_3)}\left|1\right\rangle)\left|j_3 \cdots j_n \right\rangle \end{align*} $$

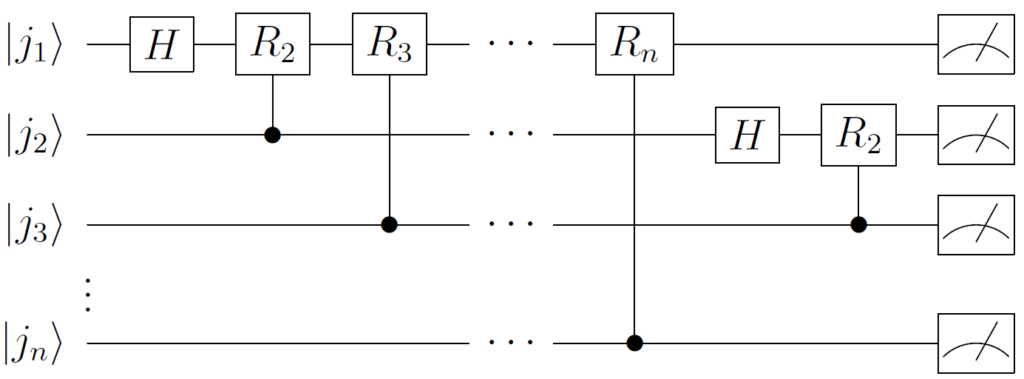
図6. 状態 $\left|j_3\right\rangle$ を制御ビット、アダマール変換後の状態 $\left|j_2\right\rangle$ を標的ビットとする $R_2$ ゲートを作用させた回路図

同じ計算を $n$ 番目の制御ビットまで繰り返すことにより、以下の状態を得ます。

$$ \frac{1}{\sqrt{2}}(\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2 \cdots j_{n-1}j_n)}\left| 1 \right\rangle) \otimes \frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi i (0.j_2\cdots j_n)}\left|1\right\rangle)\left|j_3 \cdots j_n \right\rangle $$

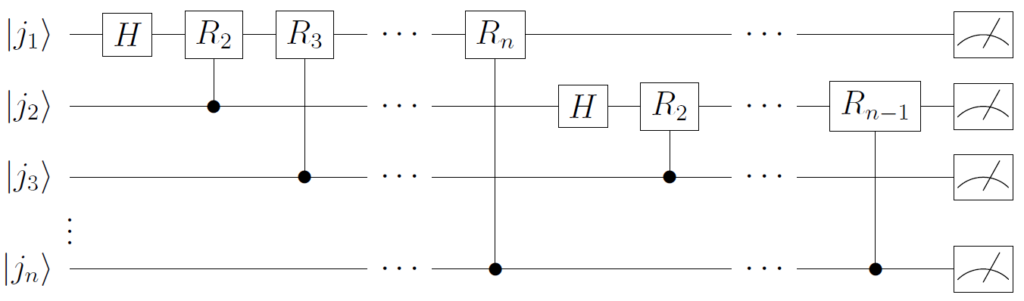
ステップC

　ステップA, Bと同様の計算を回路全体で繰り返すことにより、以下の状態を得ます。

$$ \frac{1}{\sqrt{2}}(\left| 0 \right\rangle + e^{2\pi i (0.j_1 j_2\cdots j_{n-1}j_n)}\left| 1 \right\rangle) \otimes \cdots \otimes \frac{1}{\sqrt{2}}(\left|0\right\rangle + e^{2\pi i (0.j_n)}\left|1\right\rangle) \tag{6} $$

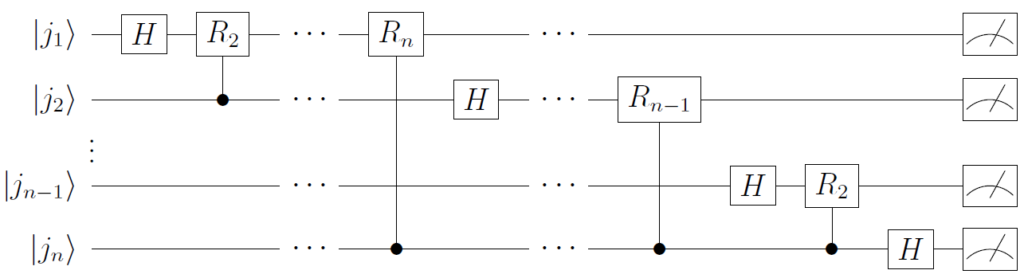
式 $(6)$ は、式 $(4)$ の右辺と積の順番が逆であることに注意が必要です。ここでは詳細は省略しますが、式 $(4)$ と同じ順序にするためにはSWAP演算を行って順序を反転させます。

結局、SWAPゲートも含めた $n$ 量子ビットの量子フーリエ変換を行う回路は以下となります。

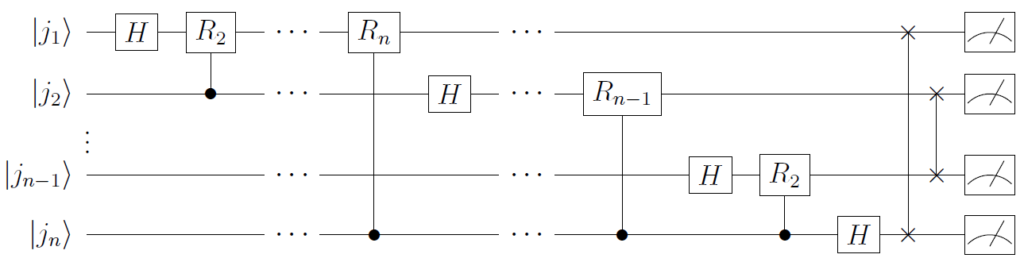
これで量子回路の導出も完了です。

おわりに

　今回は量子計算で最も重要なテクニックの一つである量子フーリエ変換について、数式と量子回路の導出を行いました。途中式や量子回路との対応について初学者向けにていねいに解説したので、参考にしていただければ幸いです。

A. 付録

A.1. 量子フーリエ変換のユニタリ性

$$ \begin{align*} \left\langle j\right|U^{\ast}_{\rm{QFT}} U_{\rm{QFT}}\left|j \right\rangle &= \frac{1}{2^n} \sum^{2^n-1}_{l=0} \sum^{2^n-1}_{k=0} e^{-2\pi i l j/2^n} e^{2\pi ikj/2^n} \left\langle l | k \right\rangle\\ &= \frac{1}{2^n} \sum^{2^n-1}_{l=0} \sum^{2^n-1}_{k=0} e^{-2\pi i l j/2^n} e^{2\pi ikj/2^n} \left\langle l | k \right\rangle \delta_{k, l} \quad \because{\left|k \right\rangle は正規直交基底} \\ &= \frac{1}{2^n} \sum^{2^n-1}_{k=0} e^{-2\pi i k j/2^n} e^{2\pi ikj/2^n} \left\langle k | k \right\rangle \\ &= \frac{1}{2^n} \sum^{2^n-1}_{k=0} 1 \\ &= 1 \\ &= \left\langle j |j \right\rangle \end{align*}$$

したがって

$$U^{\ast}_{\rm{QFT}} U_{\rm{QFT}} = I$$

であり、$U_{\rm{QFT}}$ がユニタリ行列であることが示されました。

A.2. 量子ゲートはなぜユニタリ性を要求するのか

　量子状態 $\left |i \right\rangle_t$ に対して量子ゲートによる変換 $U$ を行ったときに、変換後の状態は $\left |i \right\rangle_{t+1} = U \left |i \right\rangle_t$ で表されます。また、一般に量子状態は次のように規格化されています。

$$_t\left\langle i | i \right\rangle_t = 1, \\ \ _{t+1}\left\langle i | i \right\rangle_{t+1} = 1 $$

これより

$$ _{t}\left\langle i | U^{*} U | i \right\rangle_{t} = 1 $$

すなわち

$$ U^{*} U = I $$

が得られ、量子ゲートによる変換 $U$ がユニタリ変換である必要があることが導かれます。

参考

「暗号の理論と技術　量子時代のセキュリティ理解のために（講談社、國廣昇・編著　安田雅哉／水木敬明／高安敦／高島克幸／米山一樹／大原一真／江村恵太）
量子コンピューティング・ワークブックへようこそ！ (東京大学素粒子物理国際研究センター)
Quantum Native Dojo (株式会社QunaSys)
量子フーリエ変換のメモ

量子フーリエ変換をていねいに解説