お気軽にお問い合わせください
重回帰分析とは?数値予測の第1歩!

数値を予測する際に多用される「重回帰分析」は、売上予測や新規会員数予測などビジネスシーンで多く活用される分析手法の一つです。
本記事では、この重回帰分析の考え方やビジネスシーンでの活用方法についてわかりやすく解説いたします。
重回帰分析とは?
重回帰分析とは、予測したい数値を以下のような式(重回帰式)で表し、その式から予測の特徴を調べる分析のことをいいます。
$$y=b_1X_1+b_2X_2+b_3X_3+…+b_0$$
yは目的変数と呼ばれ、予測したい数値を表します。一方、\(X_1, X_2, …\)などを説明変数といい、目的変数を予測するのに使用する変数です。これらの説明変数は、目的変数の予測に重要と考えられる変数を使用することが一般的です。\(b_1, b_2, …\)は偏回帰係数と呼ばれ、\(b_0\)については一般的に切片と呼ばれます。この\(b_n\)の値を求めることが重回帰分析における分析のメインとなります。
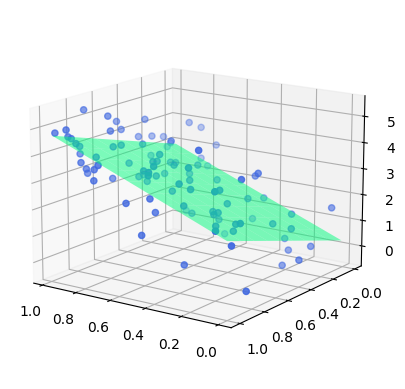
このとき、重回帰式は平面を表す
重回帰分析におけるメリットは、予測やシミュレーションなどをおこなえることです。加えて、現実の課題や仮説に即して説明変数を多く選択できることメリットです。一方でデメリットは、計算が複雑になるため、ExcelやPython、Rなどのソフトウェアを使用することが前提となります。そのため、専門家などと協力しておこなうことも重要です。
予測できる数値
重回帰分析は、連続した数値を予測することに向いた分析手法となります。後ほど具体的な利活用方法はご紹介しますが、売り上げなどに関係する「金額」の予測や、新規会員数など「人数」に関係する数値を予測することに使われます。
一方で、上記の式で表すような重回帰分析では、「5段階評価」などで表現された数値の予測や、「成功か否か」を表現した、いわゆる2値分類と呼ばれる予測には向かない分析手法となっています。
必要なデータ
重回帰分析をすることで、どんな数値が予測できるか、簡単に解説してきました。次に、どのようなデータがあると重回帰分析をすることができるかについて説明します。
重回帰分析では、目的変数と同じように連続する変数や、何かの分類やランク付けされた情報を表す変数(例:性別を0/1で表したもの、満足度を1/2/3/4/5の5段階で表したものなどです。これらは質的変数とも呼ばれます)を説明変数として扱うことができます。いずれの場合も、数値であることが必要不可欠です。
具体的な例としては、店舗の売り上げを予測するために、売り場の面積(連続値)や平均客数(連続値)、休日か否かなどを使用することができます。
このように店舗の売り上げを予測することに「寄与しそうな数値」を説明変数の候補として扱うことができます。一方で注意しなければならない点もあります。こちらについては、本記事の後半で解説いたします。
重回帰式からわかること
ここまで重回帰分析の取り扱いについて説明してきました。実際に重回帰分析を実行し、式を求めることができたら、どんなことがわかるか、について解説します。
重回帰分析をおこなって得られる重回帰式から、特徴を掴むうえで最も重要なことは、偏回帰係数の数値です。説明変数をそのまま使用して得られた偏回帰係数では、目的変数に対する説明変数の影響度合いを直接計ることはできません。それぞれの説明変数に対して「標準化」という平均を0、分散を1にする加工を加えた上で、偏回帰係数を求めることで、「標準偏回帰係数」を算出することができ、その数値を以て、説明変数同士で比較可能な影響度合いを計ることが可能となります。
影響度を見ていくうえで、まず、標準偏回帰係数の符号に注目します。マイナス(負)の符号の場合、その説明変数は目的変数に対して値を小さくするような影響を及ぼします。一方でプラス(正)の符号の場合はその逆で、目的変数を大きくするような影響を及ぼします。
次に注目するポイントは、値の大きさです。標準偏回帰係数の値がプラスであろうがマイナスであろうが、その数値は限りなく0に近い値では影響度は小さくなります。一方で標準偏回帰係数の値が大きければ大きいほど、目的変数に与える数値の影響は大きくなります。
このように、重回帰分析を実行して重回帰式を求めることができると、説明変数が目的変数に対して、「どのような(プラスかマイナス)」「どれくらい(大きさ)」影響を与えているのか知ることができます。
手順
重回帰分析をおこなうための、共通手順を紹介します。
売上や販売個数などの連続値を目的変数とします。
ドメイン知識や仮説ベース、集められそうなデータ、などの観点から重回帰モデルに使用する説明変数を選択します。
STEP1とSTEP2で選択したデータを集めます。この段階で集められないデータなどが出てくることも十分あり得ます。
重回帰分析においては多重共線性に注意する必要があります。説明変数同士などで強い相関関係などがないかこの段階で調査します。そのほかには、データの分布やばらつきなどから適切な正規化をしたり、欠損値や外れ値などの処理も行います。
基礎的な分析を経て、選択された説明変数から重回帰式を推定します。
推定された重回帰式に数値を代入して目的変数の挙動を確認したり、偏回帰係数の値を見て過学習が発生していないか、もしくは仮説と大きく異なったりしていないかなどを確認し、実用に耐えうるかを検討します。
この際、うまくいかなかったと判断される場合は、STEP2などからやり直し、上記のSTEPを繰り返していきます。
重回帰分析のビジネスシーン活用
ここからは、ビジネスシーンでの具体的な活用方法について解説します。
売上予測
今月の売り上げはいくらになるか。来月は?今期全体では?重回帰分析は企業活動の根幹をなす売り上げの予測に活用することができます。例えば、1円単位までの予測をするのではなく、アップトレンド・ダウントレンドの把握や標準偏回帰係数の特徴からKPIを策定する際に活用されることがあります。
店舗の売り上げを例に考えてみましょう。
目的変数をあるコンビニエンスストアの月間売上とします。説明変数には、周辺の人口、休日の日数、来客数、客単価、周辺の競合店舗数、顧客の滞在時間、取り扱い商品数、キャッシュレス決済有無、駐車場有無などが取り扱うことのできるデータだとします。
これらのデータを使用して重回帰分析を行うと以下のような結果になったとします。
| 説明変数 | 標準偏回帰係数の結果 |
|---|---|
| 周辺の人口 | 2.05 |
| 休日の日数 | -2.16 |
| 来客数 | 1.55 |
| 客単価 | 0.02 |
| 周辺の競合店舗数 | -1.5 |
| 顧客の滞在時間 | 3.21 |
| 取扱商品数 | 0.23 |
| キャッシュレス決済の有無 | 0.35 |
| 駐車場の有無 | -0.23 |
この時、重回帰分析の結果からおこなうことができることは以下の通りです。
- 説明変数に今月のデータを入れて、売り上げを予測する
- 標準偏回帰係数の結果から、「顧客の滞在時間」が最も影響を与えていることが分かった
- 標準偏回帰係数の結果から、「客単価」は相対的に売上には貢献していないことが分かった
- これらの結果から、滞在時間を伸ばす施策の立案を優先しておこなうこととした。
このような形で、重回帰分析を実際のビジネス現場で活用することができます。
その他にも、「新規会員数の予測」や「顧客満足度の分析」などのシーンで活用することが可能です。その際には、「必要なデータ」で紹介したデータであることと、この後ご紹介する「注意点」を踏まえることで、様々なパターンで応用可能になります。
その他の活用事例
売り上げ予測のほかに、以下のような事例があります。
- 需要予測
- 会員数予測
需要予測
重回帰分析を用いることで、需要予測にも活用することができます。基本的には上記の例の売り上げ予測と同様です。目的変数を需要数とし、説明変数を天気や気温、直近の平均需要数、店舗に関する情報などを用いることで、予測することができます。
会員数予測
重回帰分析は、会員数予測にも活用することができます。
目的変数を新規会員数として、サイトのPV数やマーケティング施策の有無などを説明変数とすることで予測することができます。売り上げ予測や需要予測と同じような考え方で活用することができます。
重回帰分析の注意点
続いては重回帰分析における注意点を説明いたします。
多重共線性(マルチコリニアリティ/Multicollinearity)
多重共線性(マルチコリニアリティ/Multicollinearity)とは、重回帰分析において最も注意すべき必要のある性質です。多重共線性が発生している重回帰式では、説明変数の評価がうまくおこなえないことに加えて、的外れな予測をしてしまうという特徴があります。そのため、多重共線性は重回帰分析において、必ず避けるべき性質なのです。
では、多重共線性はどのような状況で発生するのでしょうか。それは高い相関関係にある変数同士が、説明変数として使われている場合に発生します。
例えば、売上予測をする際に、「駅からの距離」と「駅からの徒歩時間」を説明変数に加えたとします。この時、多くの場合で多重共線性が発生します。なぜなら、駅からの距離が遠くなれば、その分駅からの徒歩時間も増えるからです。この関係性を相関関係といいます。
このように、明らかに相関関係がありそうな変数同士の場合もあれば、そうでない場合もあるため、変数が多くお互いの関係が見えにくい場合などは「相関分析」などをおこなうと良いでしょう。
欠落変数バイアス
次に欠落変数バイアスです。欠落変数バイアスは、多重共線性の逆で、重要な要素が説明変数に入っていない場合に生じる予測の偏りのことを表します。
しかし、現実的には欠落変数バイアスが起こることは避けられません。なぜならすべてのデータを集めることは不可能だからです。
欠落変数バイアスを注意点として挙げましたが、「もしかしたら変数が足りていないかもしれない」という前提に立って、重回帰分析を実施していくことが重要です。
まとめ
今回は重回帰分析について解説いたしました。
重回帰分析は、数値を予測したり、算出された回帰式からキーとなる説明変数を求めたりすることで、ビジネスの現場でも大いに活用することができます。
しかし、いかなる場合でも、その回帰式のモデル(数式)の妥当性の判断とビジネス活用する際の意思決定は、数式では行えません。あくまで重回帰分析は、人の意思決定を支える数理的な根拠として使用することが望ましいと考えられます。
重回帰分析における注意点を踏まえた、一歩深い分析の役に立てれば幸いです。
当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。重回帰分析によるモデル構築や活用の実績もございますのでお気軽にご相談ください。
研究記事も執筆しています
















