時系列分析とは？具体的な手法やビジネス活用事例を解説！

2024年11月1日2024年11月12日

時系列分析とは

時系列分析とは、時間経過・推移に伴って変化する「時系列データ」を対象とした分析手法です。
具体的なモデルとして、ARIMAモデルや状態空間モデルなどがあります。時系列分析の扱うデータは、日次・週次・月次の売り上げや来場者数などが該当します。

これらを分析することで「なぜそうなったのか≒要因分析」「これからどうなるのか≒将来予測」や「普段と違うことは起きていないか≒異常検知」などに活用することができます。

時系列データの特徴

時系列データとは、一定間隔の時間経過・推移によって観測されるデータのことであり、観測される順番に意味があるという特徴を持ちます。

また、時系列データには変動要因と呼ばれる3つの構成要素があります。

長期変動
- 長期的な増加・減少傾向がみられるもの
季節変動
- 季節的な周期、月や週単位での周期など、周期的な傾向がみられるもの
不規則変動
- 誤差など偶然によるもの、長期変動や季節変動では説明しきれないもの

さらに、以下6個の代表的な統計モデルがあります。

時系列モデルの代表的手法

ARモデル（自己回帰：Auto Regressive）
MAモデル（移動平均：Moving Average）
ARMAモデル（自己回帰移動平均：Auto Regressive Moving Average）
ARIMAモデル（自己回帰和分移動平均：Auto Regressive Integrated Moving Average）
SARIMAモデル（季節変動自己回帰和分移動平均：Seasonal Auto Regressive Integrated Moving Average）
状態空間モデル

上記のモデルをそれぞれ簡単に表すと以下のようになります。

ARモデル（自己回帰：Auto Regressive）

ARモデルは、自身の過去に回帰された形で表現されるモデルです。次の時点tを予測するために現時点t-1以前の値を用いて表現するモデルと言い換えられます。式で表すと以下の通りとなります。

$$y_t = c + \phi_1 y_{t-1} + \phi_2 y_{t-2} + \cdots + \phi_p y_{t-p} + \epsilon_t$$

$y_t$… 予測したいt時点の値
$c$…定数項
$\phi$…自己相関係数
$y_{t-1}$…予測に用いる過去の値
$\epsilon_t$…ホワイトノイズ

MAモデル（移動平均：Moving Average）

MAモデルは、時系列データのノイズ（ランダム変動）を平滑化するモデルのことをいいます。過去の誤差項の線形組み合わせを用いて現在の値を予測します。式で表すと以下の通りとなります。

$$y_t = \mu + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \cdots + \theta_q \epsilon_{t-q}$$

$y_t$… 予測したいt時点の値
$\mu$…定数項
$\theta$…自己相関係数
$\epsilon_t$…t時点のホワイトノイズ

ARMAモデル（自己回帰移動平均：Auto Regressive Moving Average）

ARMAモデルは、ARモデル（自己回帰項）とMAモデル（移動平均項）を組み合わせたもので、時系列データのトレンドとノイズの両方をモデル化し、値を予測します。式で表すと以下の通りとなります。

$$y_t = c + \phi_1 y_{t-1} + \cdots + \phi_p y_{t-p} + \epsilon_t – (\theta_1 \epsilon_{t-1} + \cdots + \theta_q \epsilon_{t-q})$$

$y_t$… 予測したいt時点の値
$c$…定数項
$\phi$…自己相関係数
$y_{t-1}$…予測に用いる過去の値
$\epsilon_t$…ホワイトノイズ
$\theta$…自己相関係数

ARIMAモデル（自己回帰和分移動平均：Auto Regressive Integrated Moving Average）

これまで説明した、AR〜ARMAモデルは、定常過程モデルでしたが、ARIMAモデルは非定常過程モデルになります。
ARIMAモデルは、d階差分系列$$\Delta^d y_t = \Delta^{d-1} y_t-\Delta^{d-1} y_{t-1}$$を以下のような式で表します。

$$\Delta^d y_t = \phi_1 \Delta^d y_{t-1} + \cdots + \phi_p \Delta^d y_{t-p} + \Delta^d \epsilon_t + \theta_1 \Delta^d\epsilon_{t-1} + \cdots + \theta_q \Delta^d\epsilon_{t-q}$$

yの階差自体に対して、ARMAモデルを適用しているということになります。このようにすることで、「定常過程」を前提としていたAR〜ARMAモデルでは適用できない「非定常過程」の時系列データに対してモデルを適用することが可能になります。

SARIMAモデル（季節変動自己回帰和分移動平均：Seasonal Auto Regressive Integrated Moving Average）

SARIMAモデルは、ARIMAモデルに対して、季節性・周期性を追加したモデルのことを指します。以下の式で表すことができます。詳細な解説は省略しますが、連続する時系列データに対してARIMAでおこなっていた計算に加え、周期性（季節性）を伴う情報に対しても同様にARIMAを適用し、その二つを重ね合わせて表現しています。

$$\phi(B) \phi_s(B) \Delta^d\Delta^D_s y_t = \theta(B) \theta_s(B) \epsilon_t$$

と表すことができます。

定常過程と非定常過程

定常過程は、時間によって平均や分散、共分散が大きく変化しない時系列データを指します。一方で、これらの特徴を持たない、長期的なアップトレンドのデータなどは非定常過程の時系列データといいます。

長期的なアップトレンドなどに代表されるように、ビジネスの現場における多くのデータは、非定常過程の時系列データです。そのため、ARIMAモデルやSARIMAモデルでモデリングするアプローチが多くなります。

状態空間モデル

状態空間モデルは、観測値同士の関係性から予測（AR〜SARIMAモデル）はせず、観測値間の関係性を状態の時系列変化とその状態から観測される値に分解して表現します。
ある時点のデータと別の時点のデータの間の関連性を分析者が想定し、対応する潜在変数（潜在的な確率変数）を考慮して分析をおこなう、ホワイトボックス的なアプローチとなります。

\begin{eqnarray}
\text{状態方程式: } x_t &=& F_t(x_{t-1})+G_t(v_t) \\
\text{観測方程式: } y_t &=& H_t(x_t)+w_t
\end{eqnarray}

$x_t$…時点tにおける、”状態”を表すxで、潜在的な確率変数のこと
$y_t$…観測値
$v_t$…ホワイトノイズ
$w_t$…ホワイトノイズ

そのほかの手法

Prophet
MMM（マーケティング・ミックス・モデリング）
BTYDモデル

分析によってわかること

時系列分析は、「将来予測」「要因分析」「異常検知」などに活用することができます。以下それぞれ解説してまいります。

将来予測

時系列分析における将来予測とは、これまでのデータから「将来売り上げはどのような推移を辿ることが予測されるか」などを明らかにすることを指します。

予測する対象が売上高などの「量的」な目的変数である場合、ARIMAなどのモデルを適用するケースが多いです。一方で、予測対象が離反or継続などの「質的」な目的変数である場合、時系列特徴量付きのテーブルデータとして扱い、線形回帰や機械学習モデルを適用するケースがあります。そのほかには生存時間分析などの手法も存在します。

要因分析

時系列分析における要因分析とは、異常が検知された要因や、なぜのその将来予測がされるのかを明らかにすることを指します。

本記事では解説していませんが、「ARIMA」や「SARIMA」の発展的モデルである「ARIMAX」や「SARIMAX」では、様々な説明変数をモデルに組み込むことができます。このことにより、予測や異常検知の「要因」を明らかにすることができます。

他には、マーケティング分野の代表的な時系列分析手法である「MMM（マーケティング・ミックス・モデリング）」では、貢献量などを算出することができます。どのような要因が予測の結果を生んでいるのかを明らかにすることができます。

異常検知

異常検知をおこなうことで、「外れ値」や「構造変化」、「変化点」の検出をすることができます。

時系列データとして使用されることの多い、予算-実績など金額に関するデータでは、月単位、四半期単位、年単位など粒度の粗いデータであることが多いです。これらに対しては、ARIMAやSARIMAなどのモデルを構築し、予測値と実績値の差（残差）から異常を検知します。

そのほかには、時系列特徴量付きのテーブルデータとして扱うことで、クラスター分析や木系アルゴリズムなどの機械学習手法を適用して、異常を検出することもできます。

お気軽にご相談ください！

当サイトの運営会社であるデータアナリティクスラボ株式会社は、データサイエンティストのプロフェッショナルサービスを提供しています。時系列分析の実績なども多数ございますのでお気軽にご相談ください。

ご相談・お問い合わせはこちらから

データアナリティクスラボに相談する

必要なデータ

時系列分析をおこなうには、時系列のデータが必要です。以下具体的なデータイメージを記載いたします。

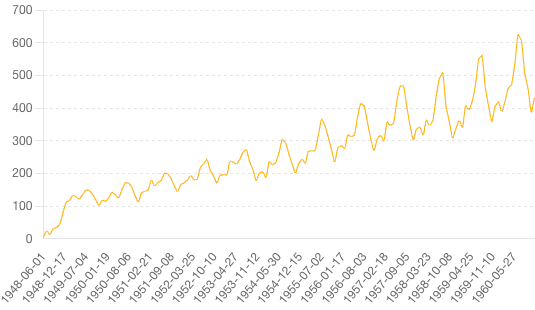
上記の可視化は、時系列データで有名な「月毎の飛行機乗客数」を示したデータを一部改変したものです。徐々に増加している「長期変動・トレンド」や周期的な変化である「季節変動」が見受けられます。

数値としては以下のようなデータになっています。

Month	Passengers
…	…
1949-01	112
1949-02	118
1949-03	132
1949-04	129
1949-05	121
…	…
1960-11	390
1960-12	432

このように、時系列（上記のMonth列）に対して、結果を示すPassengers列のような構造を持ったデータを取り扱います。Passengers列は、「売上高」であったり「登録会員数」であったりします。

このようなデータを取り扱うことで時系列分析をすることができます。

ビジネスシーンでの活用

異常検知を用いたエンタメ業界での”バズり”検出

InstagramやTikTokで『バズる』と、そのコンテンツは瞬く間に数百万再生され、大きなビジネスチャンスにつながります。SNSでの『バズり』に呼応するように、音楽サブスクリプションサービスでもコンテンツの楽曲は再生数が大きく伸びます。そのバズりにいち早く反応し、施策を展開することができれば大きなビジネスチャンスを、より現実的なものとすることができます。

これまで、音楽サブスクリプションサービス内の再生数はある程度時系列予測で予測をすることができていました。それを活用して、予測との差分がプラス方向に大きいものを『バズり』として自動的に素早く検出できるようにしたものが本事例です。

『バズり』を検出するために、予測モデルを構築しその予測値と実測値の乖離が大きい点を見つける必要があります。乖離の大きさは増加した数値の倍率や差分で表現することができます。

比較的簡単に表現することができる一方で注意が必要な点もあります。
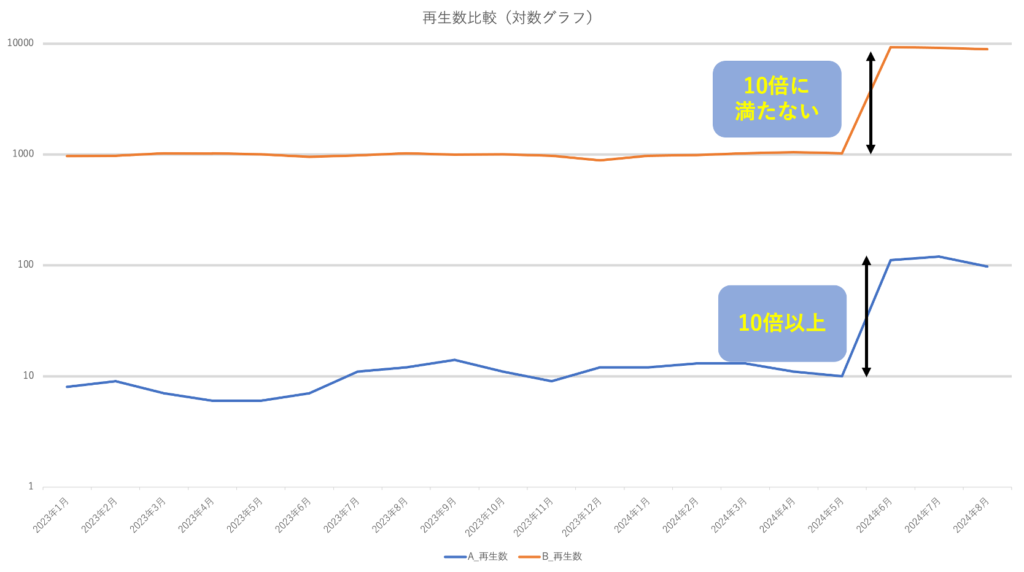
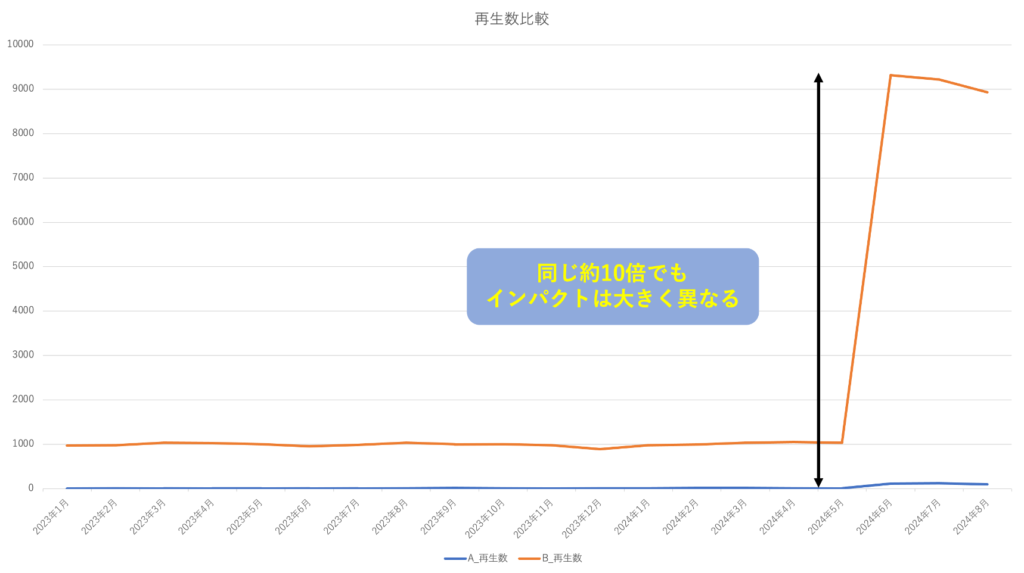
具体例として、普段の再生数が10回/日しかない楽曲が100回/日に増えることと、1,000回/日の楽曲が9,900回/日に増えた場合を考えます。
これらは倍率としてはほぼ同じですが、インパクトが大きく異なります。検知の閾値を10倍の増加とした際に、前者は10倍で検出できますが、後者は9.9倍のため検出することができません。このような事象に対しては、検出する再生数の足切りラインを設けるなどの工夫をすることで、『バズり』の実態に即した検出をすることができます。

また、時系列の予測モデルを構築する際は、季節性の要因や短期的なトレンドなどを考慮する必要があります。
季節性要因について、例えば、夏に盛り上がるサマーソング、冬にしっとりとしたクリスマスソングが、SNSやテレビで多く取り上げられるなどといった事象です。この事象をモデルに反映させる工夫が必要になります。
モデル構築の際に長期的なデータが必要となることは前提となりますが、直近のデータだけを使用した特徴量を作るなどして短期的なトレンドに対する検出感度を高める工夫も必要となります。
これらの工夫を組み込むことで、現実をより反映したモデル構築をすることができます。

また以下のような点にも注意が必要です。
再生数を予測するためには、リリースからある程度時間が経過している必要があります。つまり、リリース直後の楽曲に同じアルゴリズムを使用しても『バズり』として検出することは難しいということになります。
さらに、『バズり』が発生した場合、その後しばらく予測は安定しなくなってしまいます。『バズりを検出する』ことを最優先事項とする際は問題ありませんが、バズった後も継続してモニタリングする必要がある場合は別のアルゴリズムを検討する必要があります。

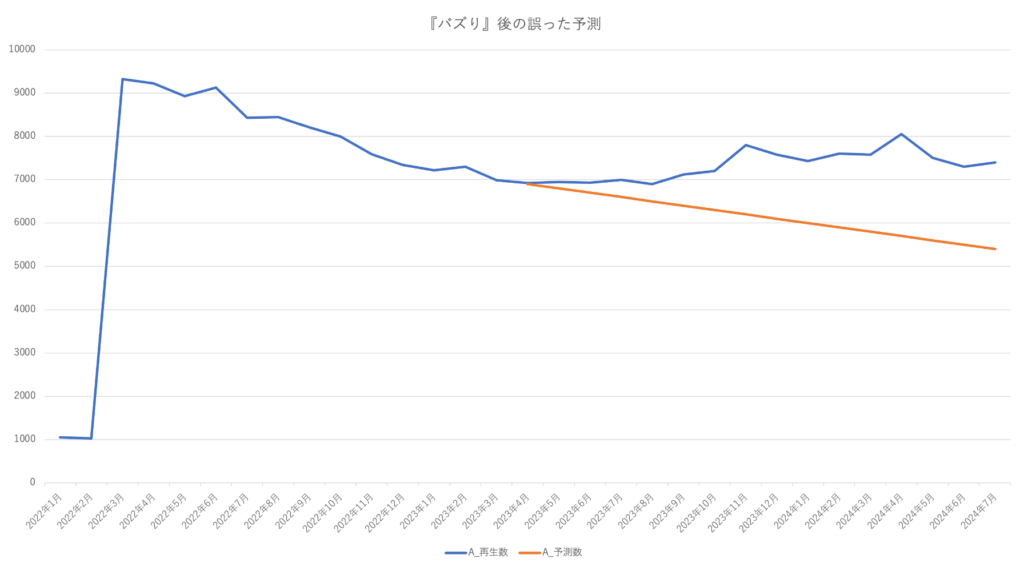
時系列分析を利用することで『バズり』の検出を可能とした事例を紹介しました。『バズり』は鮮度が重要です。その鮮度を活かすために、チャットツールなどと連携し即時通知のできる開発を併せることで、日単位のトレンドを逃すことなくマーケティング施策に活かすことができます。

お気軽にご相談ください！

ご相談・お問い合わせはこちらから

データアナリティクスラボに相談する

そのほかの活用事例

離反予測

サブスクリプションサービスや会員登録などのビジネスシーンで時系列分析による離反予測が活用されています。
具体的には、生存時間分析を実施して契約や登録が継続している確率を予測します。閾値を設けて、それを下回る時期を離反時期とみなします。

離反時期を下回らない優良顧客の特徴を分析したり、離反時期になっている顧客にはキャンペーンを実施して継続を促したりして活用されています。

故障予測

製造ラインにおける製造部品などに対して、時系列分析による故障予測が活用されています。具体的には、外れ値と構造変化を検出することによって、故障の予兆を予測します。

故障を予測することで、製造ラインが突然停止してしまうことを未然に防ぐことができます。他には、特定のベテラン社員が長年の経験から導き出していた故障の予兆を、経験の有無に関係なく誰でも検知できるようになるメリットがあります。

注意点

時系列データと点過程データ

時系列データとよく似たデータに、「点過程データ」があります。点過程データは、ある事象が発生したときに日時や時刻と一緒に生成されるデータのことを指します。
つまり、点過程データ→ローデータ、時系列データ→集計データ、のようなイメージとなり、実務上も「ローデータ（点過程データ）」を集計して「集計データ（時系列データ）」とし、分析などをおこなうことも多くあります。

データ量・粒度

時系列データを扱う際に、度々ネックになるのがデータ量とその粒度です。

月次のデータを扱う場合、1年間データを貯めても12個のデータしか集めることができません。ビジネスにおいて、データを集めるためだけに何年も長く待ち続けることは難しいでしょう。時系列データを扱う際には、データを集めるのに時間がかかるというのが前提にあることを理解する必要があります。

では、週次のデータを使えば解決するのではないでしょうか。週次のデータを使用することで12個のデータから52個のデータに増やすことができます。しかしここでデータ粒度の問題が発生します。
具体的には、月次でデータを集めた後にそれを週次のデータに変換することはできない、ということです。つまり、週次のデータを月次・年次のデータにすることはできても、その逆はできないということになります。「月次のデータしかないので分析できない」というような事態に陥りかねないように注意する必要があります。